Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 8)
-
6219 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz,cho đường thẳng \[d:\frac{{x - 2}}{2} = \frac{{y + 3}}{1} = \frac{{z - 1}}{{ - 2}}.\] Vectơ nào dưới đây là một vectơ chỉ phương của d?
 Xem đáp án
Xem đáp án
Lời giải:
Chọn đáp án B
Đường thẳng \(d:\frac{{x - 2}}{2} = \frac{{y + 3}}{1} = \frac{{z - 1}}{{ - 2}}\) có một VTCP là \(\overrightarrow u = \left( {2;1; - 2} \right)\).
Câu 2:
Cho hàm số f(x) có bảng biến thiên như sau:
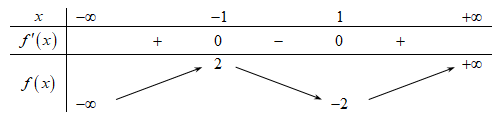
Giá trị cực tiểu của hàm số đã cho là
 Xem đáp án
Xem đáp án
Chọn đáp án C
Giá trị cực tiểu của hàm số \(f\left( x \right)\) là \( - 2\).
Câu 3:
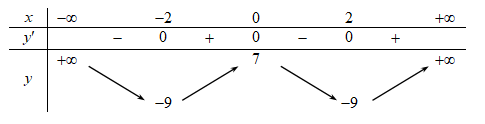
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn đáp án B
Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 2} \right)\).
Câu 4:
Trong không gian Oxyz,cho mặt phẳng \[\left( P \right):x - 6y + 12 = 0.\] Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Mặt phẳng \(\left( P \right):x - 6y + 12 = 0\) có một VTPT là \(\overrightarrow n = \left( {1; - 6;0} \right)\).
Câu 5:
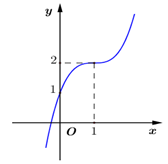
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có \(y\left( 1 \right) = 2 \Rightarrow \) Loại B và D. Mà \(y\left( 0 \right) = 1 \Rightarrow \) Chọn A.
Câu 6:
Tìm phần thực của số phức z thỏa mãn \[z\left( {1 + i} \right) - 2i = 1.\]
 Xem đáp án
Xem đáp án
Chọn đáp án B
Số phức \(z = \frac{{1 + 2i}}{{1 + i}} = \frac{3}{2} + \frac{1}{2}i\) có phần thực phần \(\frac{3}{2}\).
Câu 7:
Giới hạn \[\mathop {\lim }\limits_{x \to 1} {\mkern 1mu} \frac{{x + 2}}{{2{x^2} + 1}}\] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{x + 2}}{{2{{\rm{x}}^2} + 1}} = \frac{{1 + 2}}{{2 + 1}} = 1\).
Câu 8:
Cho hàm số f(x) có bảng biến thiên như sau:
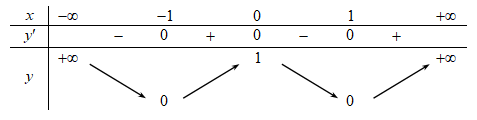
Phương trình \[4f\left( x \right) - 1 = 0\] có số nghiệm thực là
 Xem đáp án
Xem đáp án
Chọn đáp án D
Đường thẳng \(y = \frac{1}{4}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại đúng 4 điểm phân biệt.
Câu 9:
Cho hai số thực dương a và b, với \[a \ne 1.\] Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Với \(a,b >0\) và \(a \ne 1\), ta có \({\log _{{a^2}}}\left( {ab} \right) = \frac{1}{2}{\log _a}\left( {ab} \right) = \frac{1}{2}\left( {{{\log }_a}a + {{\log }_a}b} \right) = \frac{1}{2}\left( {1 + {{\log }_a}b} \right) = \frac{1}{2} + \frac{1}{2}{\log _a}b.\)
Câu 10:
Tích phân \[\int\limits_0^{\frac{\pi }{{12}}} {\sin 3xdx} \] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có \(\int\limits_0^{\frac{\pi }{{12}}} {\sin 3{\rm{xdx}}} = \left. { - \frac{{\cos 3x}}{3}} \right|_0^{\frac{\pi }{{12}}} = \frac{{2 - \sqrt 2 }}{6}\).
Câu 11:
Tính \[P = \frac{1}{{{{\log }_2}2020!}} + \frac{1}{{{{\log }_3}2020!}} + \frac{1}{{{{\log }_4}2020!}} + .... + \frac{1}{{{{\log }_{2020}}2020!}}.\]
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có \(P = {\log _{2020!}}2 + {\log _{2020!}}3 + {\log _{2020!}}4 + ... + {\log _{2020!}}2020\)
\( = {\log _{2020!}}\left( {2.3.4...2020} \right) = {\log _{2020!}}\left( {2020!} \right) = 1\).
Câu 12:
Cho khối nón (N) có đường cao bằng 4 và thể tích bằng 12π. Tính diện tích xung quanh \[{S_{xq}}\] của \[\left( N \right).\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có và
Câu 13:
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] và có đồ thị (C) như hình vẽ. Diện tích S của hình phẳng giới hạn bởi các đường \[y = f\left( x \right),{\rm{ }}y = 0,{\rm{ }}x = - 1,{\rm{ }}x = 2\] được tính theo công thức?
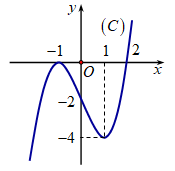
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có \(S = \int\limits_{ - 1}^2 {\left| {f\left( x \right)} \right|d{\rm{x}}} = - \int\limits_1^2 {f\left( x \right)d{\rm{x}}} \).
Câu 14:
Tính đạo hàm của hàm số \[y = \ln \left( {1 + \sqrt {2x + 1} } \right).\]
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có \(y' = \frac{1}{{1 + \sqrt {2x + 1} }}.{\left( {1 + \sqrt {2x + 1} } \right)^\prime } = \frac{1}{{1 + \sqrt {2x + 1} }}.\frac{2}{{2\sqrt {2x + 1} }} = \frac{1}{{2x + 1 + \sqrt {2x + 1} }}.\)
Câu 15:
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = \sin \left( {x + 2} \right)\] là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có \(\int {\sin \left( {x + 2} \right)dx} = - \cos \left( {x + 2} \right) + C.\)
Câu 16:
Cho phương trình phức \[{z^2} - bz + c = 0\] (\[b,{\rm{ }}c \in \mathbb{R}\]) có một nghiệm \[z = 3 + i.\] Tính \[b + c.\]
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có \({\left( {3 + i} \right)^2} - b\left( {3 + i} \right) + c = 0 \Leftrightarrow 8 + 6i - 3b - bi + c = 0\)
\( \Leftrightarrow 8 - 3b + c + \left( {6 - b} \right)i = 0 \Leftrightarrow \left\{ \begin{array}{l}6 - b = 0\\8 - 3b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\c = 10\end{array} \right. \Rightarrow b + c = 16.\)
Câu 17:
Tìm giá trị nhỏ nhất của hàm số \[y = 3x + \frac{4}{{{x^2}}}\] trên khoảng \[\left( {0; + \infty } \right).\]
 Xem đáp án
Xem đáp án
Chọn đáp án A
Hàm số đã cho xác định trên \(\left( {0; + \infty } \right)\).
Với \(x \in \left( {0; + \infty } \right)\), áp dụng bất đẳng thức Côsi ta có
Dấu “=” xảy ra \( \Leftrightarrow \frac{3}{2}x = \frac{4}{{{x^2}}} \Leftrightarrow {x^3} = \frac{8}{3} \Leftrightarrow x = \frac{2}{{\sqrt[3]{3}}}.\)
Câu 18:
Giải phương trình \[{2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {4.5^x}.\]
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có \({2^{x + 4}} + {2^{x + 2}} = {5^{x + 1}} + {4.5^x} \Leftrightarrow {2^4}{.2^x} + {2^2}{.2^x} = {5.5^x} + {4.5^x} \Leftrightarrow {20.2^x} = {9.5^x}\)
\( \Leftrightarrow {\left( {\frac{5}{2}} \right)^x} = \frac{{20}}{9} \Leftrightarrow x = {\log _{\frac{5}{2}}}\frac{{20}}{9}.\)
Câu 19:
Trong không gian Oxyz,cho hai mặt phẳng \[\left( P \right):2x - 3y + 4z + 6 = 0\] và \[\left( Q \right):2x + 3y - 4z + 5 = 0.\] Kí hiệu α là góc giữa (P) và (Q). Tính \[P = \cos \alpha .\]
 Xem đáp án
Xem đáp án
Chọn đáp án D
Mặt phẳng \(\left( P \right)\)có một VTPT là \(\overrightarrow {{n_1}} = \left( {2; - 3;4} \right)\).
Mặt phẳng \(\left( Q \right)\)có một VTPT là \(\overrightarrow {{n_2}} = \left( {2;3; - 4} \right)\).
Ta có \(P = \cos \alpha = \frac{{\left| {2.2 + \left( { - 3} \right).3 + 4.\left( { - 4} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { - 3} \right)}^2} + {4^2}} .\sqrt {{2^2} + {3^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{21}}{{29}}.\)
Câu 20:
Trong không gian Oxyz,cho hai điểm \[A\left( {1; - 3;2} \right),{\rm{ }}B\left( {2; - 2;3} \right).\] Tìm tọa độ điểm K đối xứng với A qua B.
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có B là trung điểm của đoạn thẳng AK\( \Rightarrow \left\{ \begin{array}{l}\frac{{1 + {x_K}}}{2} = 2\\\frac{{ - 3 + {y_K}}}{2} = - 2\\\frac{{2 + {z_K}}}{2} = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_K} = 3\\{y_K} = - 1\\{z_K} = 4\end{array} \right. \Rightarrow K\left( {3; - 1;4} \right)\).
Câu 21:
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn số phức z thỏa mãn \[\left| {z - 1 + 4i} \right| = 2.\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Giả sử \(z = x + yi{\rm{ }}\left( {x,y \in \mathbb{R}} \right) \Rightarrow \left| {x - 1 + \left( {y + 4} \right)i} \right| = 2 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 4} \right)^2} = 4.\)
Tập hợp các điểm biểu diễn số phức zthỏa mãn \(\left| {z - 1 + 4i} \right| = 2\) là đường tròn có tâm \(I\left( {1; - 4} \right)\)và bán kính \(R = 2\).
Câu 22:
Biết \[M\left( {1;0} \right),{\rm{ }}N\left( {0;1} \right)\] là hai điểm cực trị của đồ thị hàm số \[y = a{x^4} + b{x^2} + c.\] Tính giá trị của hàm số tại \[x = 3.\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có \(y' = 4a{x^3} + 2bx\).
Bài ra thì \(\left\{ \begin{array}{l}y\left( 1 \right) = 0\\y\left( 0 \right) = 1\\y'\left( 1 \right) = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a + b + c = 0\\c = 1\\4{\rm{a}} + 2b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 22\\b = - 2\\c = 1\end{array} \right. \Rightarrow y = {x^4} - 2{{\rm{x}}^2} + 1 \Rightarrow y\left( 3 \right) = 64\).
Câu 23:
 Xem đáp án
Xem đáp án
Chọn đáp án B
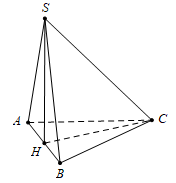
Kẻ \(SH \bot AB \Rightarrow SH \bot \left( {ABC} \right)\)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}.\frac{{AB}}{2}.\frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{24}}.\)
Câu 24:
Giải phương trình \[{\log _2}\left( {x + 12} \right).{\log _x}2 = 2.\]
 Xem đáp án
Xem đáp án
Chọn đáp án B
Điều kiện \(\left\{ \begin{array}{l}x >0\\x \ne 1\end{array} \right.\) (*).
Phương trình \( \Leftrightarrow {\log _2}\left( {x + 12} \right).\frac{1}{{{{\log }_2}x}} = 2\)
\( \Leftrightarrow {\log _2}\left( {x + 12} \right) = 2{\log _2}x \Leftrightarrow {\log _2}\left( {x + 12} \right) = {\log _2}{x^2}\)
\( \Leftrightarrow x + 12 = {x^2} \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 3\end{array} \right. \Rightarrow x = 4\) thỏa mãn (*).
Câu 25:
Cho \[F\left( x \right) = \left( {a{x^2} + bx + c} \right){e^{ - x}}\] là một nguyên hàm của hàm số \[f\left( x \right) = \left( {2{x^2} - 5x + 2} \right){e^{ - x}}\]. Giá trị của \[f\left[ {F\left( 0 \right)} \right]\] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có \(f\left( x \right) = F'\left( x \right) \Rightarrow \left( {2{x^2} - 5x + 2} \right){e^{ - x}} = \left( {2ax + b} \right){e^{ - x}} - \left( {a{x^2} + bx + c} \right){e^{ - x}}\)
\( \Rightarrow 2{x^2} - 5x + 2 = \left( {2ax + b} \right) - \left( {a{x^2} + bx + c} \right) = - a{x^2} + \left( {2a - b} \right)x + b - c\)
\( \Rightarrow \left\{ \begin{array}{l} - a = 2\\2{\rm{a}} - b = - 5\\b - c = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 1\\c = - 1\end{array} \right. \Rightarrow F\left( x \right) = \left( { - 2{{\rm{x}}^2} + x - 1} \right){e^{ - x}} \Rightarrow F\left( 0 \right) = - 1\)
\( \Rightarrow f\left[ {F\left( 0 \right)} \right] = f\left( { - 1} \right) = 9{\rm{e}}\).
Câu 26:
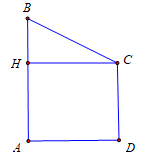
Cho hình thang \[ABCD\] có \[\widehat {BAD} = \widehat {ADC} = 90^\circ \] và \[AB = 8,{\rm{ }}CD = BC = 5.\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình thang \[ABCD\] xung quanh trục \[AB.\]
 Xem đáp án
Xem đáp án
Chọn đáp án D
Kẻ \(CH \bot AB\).
Ta có \(V = {V_{non}} + {V_{tru}} = \frac{1}{3}\pi H{C^2}.BH + \pi A{D^2}.AH.\)
\(HC = AD = \sqrt {B{C^2} - B{H^2}} = \sqrt {B{C^2} - {{\left( {AB - CD} \right)}^2}} = 4\)
\( \Rightarrow V = \frac{1}{3}\pi {.4^2}.3 + \pi {.4^2}.5 = 96\pi .\)
Câu 27:
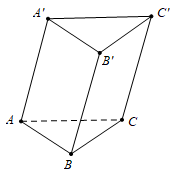
Cho lăng trụ \[ABC.A'B'C'\] có khoảng cách giữa đường thẳng \[CC'\] và mặt phẳng \[\left( {ABB'A'} \right)\] bằng 7. Mặt bên \[ABB'A'\] có diện tích bằng 4. Thể tích của khối lăng trụ \[ABC.A'B'C'\] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có \(CC'{\rm{ // }}\left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC';\left( {ABB'A'} \right)} \right) = d\left( {C;\left( {ABB'A'} \right)} \right) = 7.\)
Bài ra \({S_{ABB'A'}} = 4 \Rightarrow {S_{A'AB}} = 2\)
\( \Rightarrow {V_{ABC.A'B'C'}} = 3{V_{A'.ABC}} = 3{V_{C.A'AB}}\)
\( = 3.\frac{1}{3}d\left( {C;\left( {ABB'A'} \right)} \right).{S_{A'AB}} = 7.2 = 14.\)
Câu 28:
Cho số phức \[z = a + bi\] \[\left( {a,{\rm{ }}b \in \mathbb{R}} \right)\] thỏa mãn \[\left| {z + 1} \right| = \left| {z + 5} \right| = 2\sqrt 5 \]. Tính giá trị của biểu thức \[P = a + {b^2}.\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Giả sử \(z = a + bi{\rm{ }}\left( {a,b \in \mathbb{R}} \right)\)
Ta có \(\left\{ \begin{array}{l}\left| {z + 1} \right| = 2\sqrt 5 \\\left| {z + 5} \right| = 2\sqrt 5 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {a + bi + 1} \right| = 2\sqrt 5 \\\left| {a + bi + 5} \right| = 2\sqrt 5 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {{{\left( {a + 1} \right)}^2} + {b^2}} = 2\sqrt 5 \\\sqrt {{{\left( {a + 5} \right)}^2} + {b^2}} = 2\sqrt 5 \end{array} \right.\)
\( \Rightarrow {\left( {a + 1} \right)^2} + {b^2} = {\left( {a + 5} \right)^2} + {b^2} \Leftrightarrow a = - 3 \Rightarrow 4 + {b^2} = 20 \Leftrightarrow {b^2} = 16 \Rightarrow a + {b^2} = 13.\)
Câu 29:
Cho hàm số \[y = \frac{{2x - 1}}{{x - 1}}\] có đồ thị (C). Điểm \[M\left( {a;b} \right){\rm{ }}\left( {a >0} \right)\] thuộc (C) sao cho khoảng cách từ M tới tiệm cận đứng của (C) bằng khoảng cách M tới tiệm cận ngang của (C). Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án D
Đồ thị hàm số có tiệm cận đứng \({d_1}:x = 1\) và tiệm cận ngang \({d_2}:y = 2\).
Ta có \(M \in \left( C \right) \Rightarrow M\left( {t;\frac{{2t - 1}}{{t - 1}}} \right) \Rightarrow M\left( {t;2 + \frac{1}{{t - 1}}} \right){\rm{ }}\left( {t >0,{\rm{ }}t \ne 1} \right).\)
Bài ra có \(d\left( {M;{d_1}} \right) = d\left( {M;{d_2}} \right) \Rightarrow \left| {t - 1} \right| = \left| {2 + \frac{1}{{t - 1}} - 2} \right| \Leftrightarrow \left| {t - 1} \right| = \left| {\frac{1}{{t - 1}}} \right|\)
\( \Leftrightarrow {\left( {t - 1} \right)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 2\end{array} \right. \Rightarrow t = 2\) thỏa mãn
\( \Rightarrow M\left( {2;3} \right) \Rightarrow a + b = 5\).
Câu 30:
Trong không gian \[Oxyz\], cho điểm \[M\left( {1;0;1} \right)\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{{z - 3}}{3}\]. Đường thẳng đi qua M, vuông góc với dvà cắt Oz có phương trình là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Gọi đường thẳng cần tìm là Δ, giả sử \(N = \Delta \cap Oz \Rightarrow N\left( {0;0;z} \right)\).
\(\overrightarrow {MN} = \left( { - 1;0;z - 1} \right)\), có \(\overrightarrow {{u_d}} = \left( {1;2;3} \right)\). Do \(\Delta \bot {\rm{d}} \Rightarrow \overrightarrow {MN} .\overrightarrow {{u_d}} = 0 \Leftrightarrow - 1 + 3{\rm{z}} - 3 = 0 \Leftrightarrow z = \frac{4}{3}\).
Khi đó \(\overrightarrow {MN} = \left( { - 1;0;\frac{1}{3}} \right)\). Chọn VTCP của đường thẳng Δ là \(\overrightarrow {{u_\Delta }} = \left( { - 3;0;1} \right)\).
Phương trình đường thẳng Δ là \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 0\\z = 1 + t\end{array} \right.\).
Câu 31:
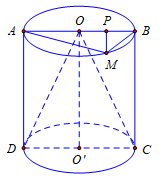
Trong không gian, cho hình trụ có thiết diện qua trục là hình vuông \[ABCD\] cạnh \[2\sqrt 3 cm\] với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung của đường tròn đáy sao cho \[\widehat {ABM} = {60^0}.\] Thể tích V của khối tứ diện \[ACDM.\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Kẻ \(MP \bot AB \Rightarrow MP \bot \left( {ABCD} \right) \Rightarrow {V_{M.ACD}} = \frac{1}{3}MP.{S_{ACD}}.\)
Ta có \(\left\{ \begin{array}{l}\sin 60^\circ = \frac{{MP}}{{MB}}\\\cos 60^\circ = \frac{{MB}}{{AB}} \Rightarrow MB = \sqrt 3 \end{array} \right. \Rightarrow MP = \frac{3}{2}cm\)
\( \Rightarrow {V_{M.ACD}} = \frac{1}{3}.\frac{3}{2}.\frac{1}{2}.{\left( {2\sqrt 3 } \right)^2} = 3c{m^3}\).
Câu 32:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \frac{{m\cos x - 16}}{{\cos x - m}}\] nghịch biến trên khoảng \[\left( {0;\frac{\pi }{3}} \right)\]?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có \(y' = \frac{{ - {m^2} + 16}}{{{{\left( {\cos x - m} \right)}^2}}}.\left( { - \sin x} \right) < 0,{\rm{ }}\forall x \in \left( {0;\frac{\pi }{3}} \right)\)(1)
Với \(\forall x \in \left( {0;\frac{\pi }{3}} \right) \Rightarrow \cos x \in \left( {\frac{1}{2};1} \right)\) nên
(1) \( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 16 < 0\\\left[ \begin{array}{l}m \ge 1\\m \le \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4 < m < 4\\\left[ \begin{array}{l}m \ge 1\\m \le \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}1 \le m < 4\\ - 4 < m \le \frac{1}{2}\end{array} \right.\).
Bài ra \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2;3; - 3; - 2; - 1;0} \right\}\).
</></>
Câu 33:
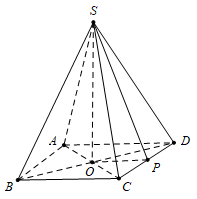
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng \[a\sqrt 2 \] và chiều cao bằng \[\frac{{a\sqrt 2 }}{2}\]. Góc giữa hai mặt phẳng \[\left( {SCD} \right)\] và \[\left( {ABCD} \right)\] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án B
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABC{\rm{D}}} \right)\).
Kẻ \(OP \bot C{\rm{D}}\), ta có \(\left\{ \begin{array}{l}C{\rm{D}} \bot {\rm{S}}O\\C{\rm{D}} \bot OP\end{array} \right. \Rightarrow C{\rm{D}} \bot \left( {SOP} \right) \Rightarrow C{\rm{D}} \bot {\rm{S}}P\).
Mà \(C{\rm{D}} \bot OP \Rightarrow \widehat {\left( {(SC{\rm{D}});(ABC{\rm{D}})} \right)} = \widehat {SPO}\).
\(\tan \widehat {SPO} = \frac{{SO}}{{OP}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{a\sqrt 2 }}{2}}} = 1 \Rightarrow \widehat {SPO} = 45^\circ \).
Câu 34:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Với 15 đôi yêu nhau thì có 30 người.
Chọn 2 người từ 30 người để bắt tay có \(C_{30}^2\) cách.
Chọn 2 bạn gái từ 15 bạn gái để bắt tay có \(C_{15}^2\) cách.
15 bạn trai bắt tay với bạn gái của mình có 15 cái bắt tay.
Vậy có tất cả \(C_{30}^2 - C_{15}^2 - 15 = 315\)cái bắt tay.
Câu 35:
Cho hàm số f(x) liên tục trên \[\mathbb{R}\] thỏa mãn \[\int\limits_1^9 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}dx} = 4\] và \[\int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\cos xdx} = 2\]. Tính tích phân \[I = \int\limits_0^3 {f\left( x \right)dx} \].
 Xem đáp án
Xem đáp án
Chọn đáp án D
Đặt \(t = \sqrt x \Rightarrow dt = \frac{{d{\rm{x}}}}{{2\sqrt x }} \Rightarrow \left\{ \begin{array}{l}x = 1,t = 1\\x = 9,t = 3\end{array} \right. \Rightarrow \int\limits_1^9 {\frac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}d{\rm{x}}} = 2\int\limits_1^3 {f\left( t \right)dt} = 4 \Rightarrow \int\limits_1^3 {f\left( x \right)d{\rm{x}}} = 2\).
Đặt \(t = \sin x \Rightarrow dt = \cos xdx \Rightarrow \left\{ \begin{array}{l}x = 0,t = 0\\x = \frac{\pi }{2},t = 1\end{array} \right. \Rightarrow \int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\cos xdx} = \int\limits_0^1 {f\left( t \right)dt} = 2 \Leftrightarrow \int\limits_0^1 {f\left( x \right)dx} = 2\).
Suy ra \(I = \int\limits_0^3 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^3 {f\left( x \right)d{\rm{x}}} = 4\).
Câu 36:
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng \[\left( P \right):2x - 5y - z = 0\] và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{{y + 1}}{1} = \frac{{z - 3}}{{ - 1}}.\] Viết phương trình đường thẳng Δ vuông góc mặt phẳng (P) tại giao điểm của đường thẳng dvà mặt phẳng (P).
 Xem đáp án
Xem đáp án
Chọn đáp án D
Gọi \(M = d \cap \left( P \right)\), ta có \(d:\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + t\\z = 3 - t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right) \Rightarrow M\left( {t + 1;t - 1;3 - t} \right)\).
Điểm \[M \in \left( P \right) \Rightarrow 2\left( {t + 1} \right) - 5\left( {t - 1} \right) - \left( {3 - t} \right) = 0 \Leftrightarrow - 2t + 4 = 0 \Leftrightarrow t = 2 \Rightarrow M\left( {3;1;1} \right).\]
Mặt phẳng \(\left( P \right)\) có một VTPT là \(\overrightarrow n = \left( {2; - 5; - 1} \right)\).
Ta có \(\Delta \bot \left( P \right) \Rightarrow \Delta \) nhận \(\overrightarrow n = \left( {2; - 5; - 1} \right)\) là một VTCP.
Kết hợp với Δ qua \(M\left( {3;1;1} \right) \Rightarrow \Delta :\frac{{x - 3}}{2} = \frac{{y - 1}}{{ - 5}} = \frac{{z - 1}}{{ - 1}}.\)
Câu 37:
Cho hình chóp \[S.{\mkern 1mu} ABCD\] có đáy \[ABCD\] là hình chữ nhật, \[AB = a,{\mkern 1mu} {\mkern 1mu} BC = 2a.\] Cạnh \[SA = 2a\] và vuông góc với mặt phẳng \[\left( {ABCD} \right).\] Khoảng cách giữa hai đường thẳng BD và SC bằng
 Xem đáp án
Xem đáp án
Chọn đáp án D
Dựng hình bình hành DBCPnhư hình vẽ.
Từ \(B{\rm{D // CP}} \Rightarrow {\rm{BD // }}\left( {SCP} \right) \Rightarrow d\left( {B{\rm{D}};SC} \right) = d\left( {D;(SCP)} \right) = \frac{1}{2}d\left( {A;(SCP)} \right)\).
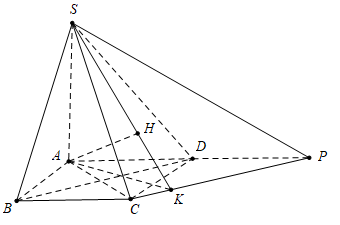 Kẻ \(AK \bot CP,{\rm{ }}AH \bot SK \Rightarrow d\left( {A;\left( {SCP} \right)} \right) = AH\)
Kẻ \(AK \bot CP,{\rm{ }}AH \bot SK \Rightarrow d\left( {A;\left( {SCP} \right)} \right) = AH\)
\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH.\)
Ta có \({S_{ACP}} = \frac{1}{2}AK.CP = \frac{1}{2}CD.AP = \frac{1}{2}a.4a = 2{a^2}.\)
Cạnh \(CP = BD = \sqrt {A{B^2} + A{D^2}} = a\sqrt 5 \Rightarrow AK = \frac{{4a}}{{\sqrt 5 }}.\)
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{4{a^2}}} + \frac{5}{{16{a^2}}} \Rightarrow AH = \frac{{4a}}{3}\)
\( \Rightarrow d\left( {BD;SC} \right) = \frac{1}{2}AH = \frac{{2a}}{3}.\)
Câu 38:
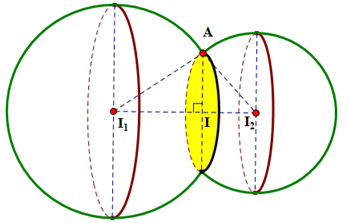
Trong không gian Oxyz,cho mặt cầu \[\left( {{S_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 16\] và \[\left( {{S_2}} \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9\] cắt nhau theo giao tuyến là đường tròn (C). Tìm tọa độ tâm của đường tròn (C).
 Xem đáp án
Xem đáp án
Chọn đáp án D
Mặt cầu \(\left( {{S_1}} \right)\) có tâm \({I_1}\left( {1;1;2} \right)\) và bán kính \({R_1} = 4\).
Mặt cầu \(\left( {{S_2}} \right)\) có tâm \({I_2}\left( { - 1;2; - 1} \right)\) và bán kính \({R_2} = 3\).
Ta có \(\overrightarrow {{I_1}{I_2}} = \left( { - 2;1; - 3} \right) \Rightarrow {I_1}{I_2} = \sqrt {14} \).
Gọi Ilà tâm của đường tròn giao tuyến \(\left( C \right)\) và Alà một điểm thuộc \(\left( C \right)\).
Ta có \(16 - 9 = - 4{\rm{x}} + 2y - 6{\rm{z}} \Leftrightarrow 4{\rm{x}} - 2y + 6{\rm{z}} + 7 = 0\).
Gọi \(\left( P \right)\) là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu \(\left( {{S_1}} \right)\) và \(\left( {{S_2}} \right)\)
\( \Rightarrow \left( P \right):4{\rm{x}} - 2y + 6{\rm{z}} + 7 = 0 \Rightarrow {I_1}I = d\left( {{I_1};(P)} \right) = \frac{{21}}{{2\sqrt {14} }}\).
\(\overrightarrow {{I_1}I} = \frac{{\left| {\overrightarrow {{I_1}I} } \right|}}{{\left| {\overrightarrow {{I_1}{I_2}} } \right|}}.\overrightarrow {{I_1}{I_2}} = \frac{{\frac{{21}}{{2\sqrt {14} }}}}{{\sqrt {14} }}.\overrightarrow {{I_1}{I_2}} = \frac{3}{4}.\overrightarrow {{I_1}{I_2}} \Leftrightarrow \left\{ \begin{array}{l}{x_I} - 1 = \frac{3}{4}.\left( { - 2} \right)\\{y_I} - 1 = \frac{3}{4}.1\\{z_I} - 2 = \frac{3}{4}.\left( { - 3} \right)\end{array} \right. \Rightarrow I\left( { - \frac{1}{2};\frac{7}{4}; - \frac{1}{4}} \right)\).
\({I_1}I = {I_1}A.\cos \widehat {A{I_1}I} = {R_1}.\cos \widehat {A{I_1}{I_2}}\)
\( = {R_1}.\frac{{{I_1}{A^2} + {I_1}I_2^2 - AI_2^2}}{{2.{I_1}A.{I_1}{I_2}}} = 4.\frac{{{4^2} + 14 - {3^2}}}{{2.4.\sqrt {14} }} = \frac{{21}}{{2\sqrt {14} }}.\)
Câu 39:
Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ. Bất phương trình \[f\left( x \right) < x + m\] đúng với mọi \[x \in \left( {0;1} \right)\] khi và chỉ khi
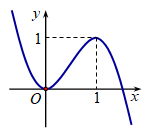
</>
 Xem đáp án
Xem đáp án
Chọn đáp án A
Xét hàm số \(g\left( x \right) = f\left( x \right) - x,{\rm{ }}x \in \left( {0;1} \right) \Rightarrow g'\left( x \right) = f'\left( x \right) - 1.\)
Từ hình vẽ, ta thấy với mọi \(x \in \left( {0;1} \right)\)thì \(0 < f'\left( x \right) < 1 \Rightarrow f'\left( x \right) - 1 < 0\)
\( \Rightarrow g'\left( x \right) < 0,\forall x \in \left( {0;1} \right) \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( {0;1} \right) \Rightarrow g\left( x \right) < g\left( 0 \right) = f\left( 0 \right).\)
Khi đó \(m >g\left( x \right)\) có nghiệm với mọi \(x \in \left( {0;1} \right) \Leftrightarrow m \ge f\left( 0 \right)\).
Câu 40:
Cho phương trình \[{x^3} + 2{m^3} = 3{m^2}.\sqrt[3]{{3{m^2}x - 2{m^3}}}\] (m là tham số thực) có tổng các nghiệm thực bằng 10. Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta thấy \(m = 0\) không thỏa mãn phương trình.
Với \(m \ne 0 \Rightarrow {\left( {\frac{x}{m}} \right)^3} + 2 = 3\sqrt[3]{{3.\frac{x}{m} - 2}}\).
Đặt \(u = \frac{x}{m} \Rightarrow {u^3} + 2 = 3\sqrt[3]{{3u - 2}}\).
Đặt \(\sqrt[3]{{3u - 2}} = v \Rightarrow \left\{ \begin{array}{l}{u^3} + 2 = 3v\\{v^3} + 2 = 3u\end{array} \right. \Rightarrow {u^3} + 3u = {v^3} + 3v \Leftrightarrow u = v \Rightarrow {u^3} + 2 = 3u \Rightarrow \left[ \begin{array}{l}u = 1\\u = - 2\end{array} \right.\).
\( \Rightarrow \left[ \begin{array}{l}\frac{x}{m} = 1\\\frac{x}{m} = - 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = m\\x = - 2m\end{array} \right. \Rightarrow m + \left( { - 2m} \right) = 10 \Rightarrow m = - 10.\)
Câu 41:
Biết rằng \[{2^{x + \frac{1}{x}}} = {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right]\] trong đó \[x >0.\] Tính giá trị của biểu thức \[P = {x^2} + {y^2} - xy + 1.\]
 Xem đáp án
Xem đáp án
Chọn đáp án C
Ta có \({2^{x + \frac{1}{x}}} \ge {2^2} \Rightarrow {\log _2}\left[ {14 - \left( {y - 2} \right)\sqrt {y + 1} } \right] \ge 4 \Rightarrow \left( {y - 2} \right)\sqrt {y + 1} \le - 2.\)
Đặt \(t = \sqrt {y + 1} \ge 0 \Rightarrow t\left( {{t^2} - 3} \right) \le - 2 \Leftrightarrow \left( {t - 1} \right)\left( {{t^2} + t - 2} \right) \le 0 \Leftrightarrow {\left( {t - 1} \right)^2}\left( {t + 2} \right) \le 0 \Rightarrow t = 1\)
\( \Rightarrow \sqrt {y + 1} = 1 \Rightarrow y = 0 \Rightarrow x = 1.\)
Câu 42:
Trong kì thi thử THPT Quốc Gia, Lan làm để thi trắc nghiệm môn Toán. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2điểm. Lan trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại Lan chọn ngẫu nhiên. Tính xác suất để điểm thi môn Toán của Lan không dưới 9,5 điểm.
 Xem đáp án
Xem đáp án
Chọn đáp án B
Để điểm thi môn Toán của Lan không dưới 9,5 điểm thì bạn ấy phải chọn đúng ít nhất 3 câu trong 5 câu còn lại.
Xác suất mỗi câu chọn đúng là \(\frac{1}{4}\) và không chọn đúng là \(\frac{3}{4}\).
+ TH1: Thảo trả lời đúng 3 câu trong 5 câu còn lại, xác suất là \({p_1} = {\left( {\frac{1}{4}} \right)^3}.{\left( {\frac{3}{4}} \right)^2}\).
+ TH2: Thảo trả lời đúng 4 câu trong 5 câu còn lại, xác suất là \({p_2} = {\left( {\frac{1}{4}} \right)^4}.\left( {\frac{3}{4}} \right)\).
+ TH3: Thảo trả lời đúng cả 5 câu trong 5 câu còn lại, xác suất là \({p_3} = {\left( {\frac{1}{4}} \right)^5}\).
Vậy xác suất cần tìm là \({p_1} + {p_2} + {p_3} = \frac{{13}}{{1024}}\).
Câu 43:
Cho hình chóp \[S.ABC\] có cạnh \[BC = 3a\] và \[SA\] vuông góc với mặt phẳng \[\left( {ABC} \right)\]. Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Biết cạnh \[MN = \frac{{9a\sqrt 2 }}{5}\], tính tỉ số \[\frac{{{V_{S.AMN}}}}{{{V_{A.BMNC}}}}.\]
 Xem đáp án
Xem đáp án
Chọn đáp án D
Ta có \(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SA}}{{SA}}.\frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{SC}}\)(1)
Lại có \(S{A^2} = SM.SB\) và \(S{A^2} = SN.SC\)
\( \Rightarrow SM.SB = SN.SC \Rightarrow \frac{{SM}}{{SC}} = \frac{{SN}}{{SB}}\)
\( \Rightarrow \Delta SMN\~\Delta SCB{\rm{ }}\left( {c - g - c} \right) \Rightarrow \frac{{SM}}{{SC}} = \frac{{SN}}{{SB}} = \frac{{MN}}{{CB}}.\)
Khi đó từ (1) \( \Rightarrow \frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SC}}.\frac{{SN}}{{SB}} = \frac{{MN}}{{BC}}.\frac{{MN}}{{BC}} = \frac{{M{N^2}}}{{B{C^2}}}.\)
Bài ra \(MN = \frac{{9a\sqrt 2 }}{5}\) và \(BC = 3a \Rightarrow \frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{18}}{{25}} \Rightarrow {V_{S.AMN}} = \frac{{18}}{{25}}{V_{S.ABC}}\)
\( \Rightarrow {V_{A.BMNC}} = {V_{S.ABC}} - {V_{S.AMN}} = {V_{S.ABC}} - \frac{{18}}{{25}}{V_{S.ABC}} = \frac{7}{{25}}{V_{S.ABC}} \Rightarrow \frac{{{V_{S.AMN}}}}{{{V_{A.BMNC}}}} = \frac{{18}}{7}.\)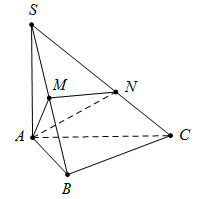
Câu 44:
Cho phương trình \[f\left( x \right) = {x^3} - 3{x^2} - 6x + 1.\] Số nghiệm thực của phương trình \[\sqrt {f\left( {f\left( x \right) + 1} \right) + 1} = f\left( x \right) + 2\] là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Đặt \(t = f\left( x \right) + 1 \Rightarrow t = {x^3} - 3{{\rm{x}}^2} - 6{\rm{x}} + 2\).
Ta có \(\sqrt {f\left( t \right) + 1} = t + 1 \Leftrightarrow \left\{ \begin{array}{l}t \ge - 1\\f\left( t \right) + 1 = {\left( {t + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \ge - 1\\\left( {{t^3} - 3{t^2} - 6t + 1} \right) + 1 = {t^2} + 2t + 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}t \ge - 1\\{t^3} - 4{t^2} - 8t + 1 = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}t = {t_1} \approx 5,44\\t = {t_2} \approx 0,12\end{array} \right. \Rightarrow \left[ \begin{array}{l}f\left( x \right) = {t_1} - 1 \approx 4,44\\f\left( x \right) = {t_2} - 1 \approx - 0,88\end{array} \right.\)
Ta có \(f'\left( x \right) = 3{{\rm{x}}^2} - 6{\rm{x}} - 6 = 0 \Rightarrow x = 1 \pm \sqrt 3 \).
Xét bảng sau:
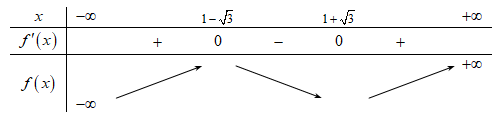
Tính \(f\left( {1 - \sqrt 3 } \right) = 6\sqrt 3 - 6 \approx 4,39;{\rm{ f}}\left( {1 + \sqrt 3 } \right) = - 6 - \sqrt 6 \approx - 16,39\).
Từ đó \(f\left( x \right) = {t_1} - 1\) có đúng 1 nghiệm và \(f\left( x \right) = {t_2} - 1\) có đúng 3 nghiệm phân biệt (khác nghiệm nói trên).
Câu 45:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số \[y = \left| {f\left( {x - 2020} \right) + m} \right|\] có đúng 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
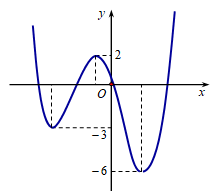
 Xem đáp án
Xem đáp án
Chọn đáp án A
Số điểm cực trị của \(y = \left| {f\left( {x - 2020} \right) + m} \right|\)bằng số điểm cực trị của \(y = \left| {f\left( x \right) + m} \right|\).
Đặt \(g\left( x \right) = f\left( x \right) + m \Rightarrow g\left( x \right)\) có đúng 3 điểm cực.
Khi đó \(g\left( x \right) = 0\) cần có 2 nghiệm phân biệt (không tính 3 điểm cực trị nói trên).
\( \Leftrightarrow \left[ \begin{array}{l} - m \ge 2\\ - 6 < - m \le - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le - 2\\3 \le m < 6\end{array} \right. \Rightarrow m \in \left\{ {3;4;5} \right\}\).
</>
Câu 46:
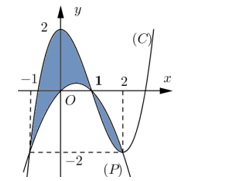
Hình phẳng \[\left( H \right)\] được giới hạn bởi đồ thị (C) của hàm số đa thức bậc ba và parabol \[\left( P \right)\] có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
 Xem đáp án
Xem đáp án
Chọn đáp án A
Giả sử hàm bậc 3 là \(f\left( x \right) = a{x^3} + b{x^2} + cx + d \Rightarrow f'\left( x \right) = 3a{x^2} + 2bx + c\)
Do đồ thị hàm số đạt cực đại tại \(A\left( {0;2} \right)\) và cực tiểu tại \(B\left( {2; - 2} \right)\) nên ta có hệ
\(\left\{ \begin{array}{l}f\left( 0 \right) = 2\\f'\left( 0 \right) = 0\\f\left( 2 \right) = - 2\\f'\left( 2 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}d = 2\\c = 0\\8{\rm{a}} + 4b + 2 = - 2\\12{\rm{a}} + 4b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}d = 2\\c = 0\\a = 1\\b = - 3\end{array} \right.\). Từ đây ta suy ra \(f\left( x \right) = {x^3} - 3{{\rm{x}}^2} + 2\).
Gọi phương trình \(\left( P \right)\) là \(y = g\left( x \right)\) thế thì \(S = \int\limits_{ - 1}^1 {\left( {f(x) - g(x)} \right)d{\rm{x}}} + \int\limits_1^2 {\left( {g(x) - f(x)} \right)d{\rm{x}}} \)
Vì \(f\left( x \right)\) là hàm bậc ba, còn \(g\left( x \right)\) là hàm bậc hai mà hai đồ thị cắt nhau tại ba điểm có hoành độ là \(x = - 1\); \(x = 1\); \(x = 2\) nên \(f\left( x \right) - g\left( x \right) = \left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right) = {x^3} - 2{{\rm{x}}^2} - x + 2\).
Vậy \(S = \int\limits_{ - 1}^1 {\left( {{x^3} - 2{{\rm{x}}^2} - x + 2} \right)d{\rm{x}}} + \int\limits_1^2 { - \left( {{x^3} - 2{{\rm{x}}^2} - x + 2} \right)d{\rm{x}}} = \frac{{37}}{{12}}\).
Câu 47:
Cho phương trình \[{6^x} + m = {\log _6}\left( {x - m} \right)\] (m là tham số thực). Có bao nhiêu giá trị nguyên thuộc khoảng \[\left( { - 6;12} \right)\] của m để phương trình đã cho có nghiệm?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Điều kiện: \(x >m\) (*). Đặt \({\log _6}\left( {x - m} \right) = y \Rightarrow \left\{ \begin{array}{l}x - m = {6^y}\\{6^x} + m = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{6^y} + m = x\\{6^x} + m = y\end{array} \right.\)
\( \Rightarrow {6^x} + m + x = {6^y} + m + y \Leftrightarrow {6^x} + x = {6^y} + y \Leftrightarrow x = y \Rightarrow m = x - {6^x}.\)
Xét hàm số \(f\left( x \right) = x - {6^x},x \in \mathbb{R}\) có \(f'\left( x \right) = 1 - {6^x}\ln 6 = 0 \Rightarrow {6^x} = \frac{1}{{\ln 6}} \Rightarrow x = {\log _6}\frac{1}{{\ln 6}}.\)
Xét bảng sau, trong đó \({x_0} = {\log _6}\frac{1}{{\ln 6}}\).
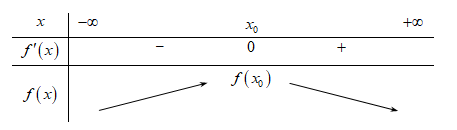
Từ bảng trên, ta được \(m \le f\left( {{x_0}} \right)\) thỏa mãn hay \(m \le f\left( {{{\log }_6}\frac{1}{{\ln 6}}} \right){\rm{ }}\left( { \approx - 0,325} \right)\).
Kết hợp với \(m \in \left( { - 6;12} \right),{\rm{ }}m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 5; - 4; - 3;...; - 1} \right\}.\)
Câu 48:
Cho hàm số f(x) thỏa mãn \[{\left[ {f'\left( x \right)} \right]^3} + {x^2}.f'\left( x \right) = 2{x^3} + 4{x^2} + 3x + 1,\forall x \in \mathbb{R}\] và \[f\left( 0 \right) = 2.\] Tích phân \[\int\limits_0^6 {f\left( x \right)dx} \] bằng
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có \({\left[ {f'\left( x \right)} \right]^3} + {x^2}.f'\left( x \right) = 2{x^3} + 4{x^2} + 3x + 1 = {\left( {x + 1} \right)^3} + {x^2}\left( {x + 1} \right)\)
\( \Rightarrow {\left[ {f'\left( x \right)} \right]^3} - {\left( {x + 1} \right)^3} + {x^2}\left[ {f'\left( x \right) - x - 1} \right] = 0\)
\( \Rightarrow \left[ {f'\left( x \right) - x - 1} \right].\left[ {{{\left( {f'\left( x \right)} \right)}^2} + \left( {x + 1} \right).f'\left( x \right).{{\left( {x + 1} \right)}^2} + {x^2}} \right] = 0\)(1)
Lại có \({\left( {f'\left( x \right)} \right)^2} + \left( {x + 1} \right).f'\left( x \right).{\left( {x + 1} \right)^2} + {x^2} = {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} \ge 0,\forall x \in \mathbb{R}.\)
Dấu “=” xảy ra \( \Leftrightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} = \frac{3}{4}{\left( {x + 1} \right)^2} = {x^2} = 0.\)
Đây là điều kiện vô lý nên dấu “=” không xảy ra \( \Rightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} >0,\forall x \in \mathbb{R}\)
Do đó (1) \( \Leftrightarrow f'\left( x \right) = x + 1 \Rightarrow f\left( x \right) = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C.\)
Mà \[f\left( 0 \right) = 2 \Rightarrow C = 2 \Rightarrow f\left( x \right) = \frac{{{x^2}}}{2} + x + 2 \Rightarrow \int\limits_0^6 {f\left( x \right)dx} = \left. {\left( {\frac{{{x^3}}}{6} + \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^6 = 66.\]
Câu 49:
Cho hai số phức \[{z_1}\], \[{z_2}\] thỏa mãn \[\left| {{z_1} + 2 - 3i} \right| = 2\] và \[\left| {\overline {{z_2}} - 1 - 2i} \right| = 1\]. Tìm giá trị lớn nhất của \[\left| {{z_1} - {z_2}} \right|\].
 Xem đáp án
Xem đáp án
Chọn đáp án B
Ta có \({\left[ {f'\left( x \right)} \right]^3} + {x^2}.f'\left( x \right) = 2{x^3} + 4{x^2} + 3x + 1 = {\left( {x + 1} \right)^3} + {x^2}\left( {x + 1} \right)\)
\( \Rightarrow {\left[ {f'\left( x \right)} \right]^3} - {\left( {x + 1} \right)^3} + {x^2}\left[ {f'\left( x \right) - x - 1} \right] = 0\)
\( \Rightarrow \left[ {f'\left( x \right) - x - 1} \right].\left[ {{{\left( {f'\left( x \right)} \right)}^2} + \left( {x + 1} \right).f'\left( x \right).{{\left( {x + 1} \right)}^2} + {x^2}} \right] = 0\)(1)
Lại có \({\left( {f'\left( x \right)} \right)^2} + \left( {x + 1} \right).f'\left( x \right).{\left( {x + 1} \right)^2} + {x^2} = {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} \ge 0,\forall x \in \mathbb{R}.\)
Dấu “=” xảy ra \( \Leftrightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} = \frac{3}{4}{\left( {x + 1} \right)^2} = {x^2} = 0.\)
Đây là điều kiện vô lý nên dấu “=” không xảy ra \( \Rightarrow {\left[ {f'\left( x \right) + \frac{{x + 1}}{2}} \right]^2} + \frac{3}{4}{\left( {x + 1} \right)^2} + {x^2} >0,\forall x \in \mathbb{R}\)
Do đó (1) \( \Leftrightarrow f'\left( x \right) = x + 1 \Rightarrow f\left( x \right) = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C.\)
Mà \[f\left( 0 \right) = 2 \Rightarrow C = 2 \Rightarrow f\left( x \right) = \frac{{{x^2}}}{2} + x + 2 \Rightarrow \int\limits_0^6 {f\left( x \right)dx} = \left. {\left( {\frac{{{x^3}}}{6} + \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^6 = 66.\]
Câu 50:
Trong không gian Oxyz,cho hai điểm \[M\left( { - 2; - 2;1} \right),\] \[A\left( {1;2; - 3} \right)\] và đường thẳng \[d:\frac{{x + 1}}{2} = \frac{{y - 5}}{2} = \frac{z}{{ - 1}}\]. Tìm một vectơ chỉ phương \[\vec u{\mkern 1mu} {\mkern 1mu} \] của đường thẳng Δ đi qua M, vuông góc với đường thẳng dđồng thời cách điểm A một khoảng bé nhất.
 Xem đáp án
Xem đáp án
Chọn đáp án A
Điểm \(M\left( {x;y} \right)\) biểu diễn số phức \({z_1} = x + yi{\rm{ }}\left( {x,y \in \mathbb{R}} \right) \Rightarrow \left| {x + yi + 2 - 3i} \right| = 2\)
\( \Rightarrow M\) thuộc đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( { - 2;3} \right)\) và bán kính \({R_1} = 2\).
Điểm \(N\left( {x';y'} \right)\) biểu diễn số phức \({z_2} = x' + y'.i{\rm{ }}\left( {x',y' \in \mathbb{R}} \right) \Rightarrow \left| {x' - y'.i - 1 - 2i} \right| = 1\)
\( \Rightarrow N\) thuộc đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {1; - 2} \right)\) và bán kính \({R_2} = 1\).
Như vậy \(\left| {{z_1} - {z_2}} \right| = MN\). Ta có \(\overrightarrow {{I_1}{I_2}} = \left( {3; - 5} \right) \Rightarrow {I_1}{I_2} = \sqrt {34} >{R_1} + {R_2}\)
\( \Rightarrow \left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) ở ngoài nhau \( \Rightarrow M{N_{\max }} = {I_1}{I_2} + {R_1} + {R_2} = \sqrt {34} + 3\).
