Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau:
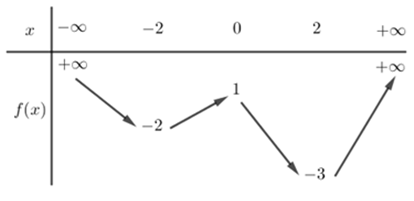
Xác định số nghiệm của phương trình \[\left| {f\left( {{x^3} - 3{x^2}} \right)} \right| = \frac{3}{2}\], biết \[f\left( { - 4} \right) = 0\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Đặt \[t = {x^3} - 3{x^2}\], ta có \[t' = 3{x^2} - 6x;t' = 0\left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\]
Bảng biến thiên (1):
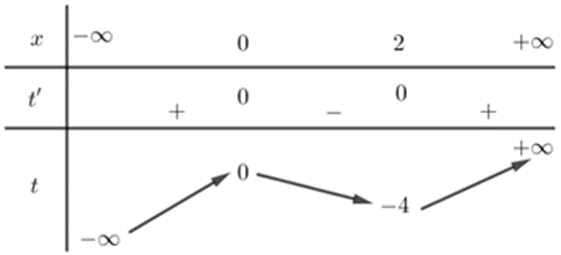
Phương trình đã cho trở thành
Từ giả thiết, ta có bảng biến thiên (2) của hàm số \[y = f\left( x \right)\]:
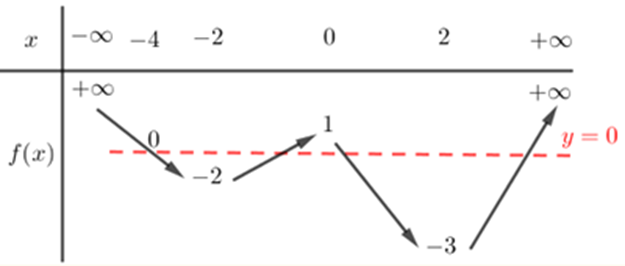
Dựa vào bảng biến thiên (2), ta có
+) . Dựa vào bảng biến thiên (1), ta có phương trình (1.1) có 1 nghiệm và phương trình (1.2) có 1 nghiệm (các nghiệm này không trùng nhau).
Dựa vào bảng biến thiên (1), ta có phương trình (2.1) có 3 nghiệm; phương trình (2.2) có 3 nghiệm; phương trình (2.3) có 1 nghiệm; phương trình (2.4) có 1 nghiệm (các nghiệm này không trùng nhau và không trùng với các nghiệm của phương trình \[f\left( t \right) = \frac{3}{2}\]).
Vậy phương trình đã cho có 10 nghiệm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Với a là số thực dương tùy ý, \[{\log _2}\left( {8a} \right)\] bằng
Cho hai số thực \[a,b > 1\] sao cho tồn tại số thực \[x\left( {x > 0,x \ne 1} \right)\] thỏa mãn \[{a^{{{\log }_b}}}x = {b^{{{\log }_a}{x^2}}}\]. Khi biểu thức \[P = {\ln ^2}a + {\ln ^2}b - \ln \left( {ab} \right)\] đạt giá trị nhỏ nhất thì \[a + b\] thuộc khoảng nào dưới đây?
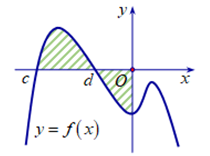
Diện tích phần hình phẳng gạch chéo như hình vẽ được tính theo công thức nào dưới đây?
Kí hiệu \[{z_1},{z_2}\] là hai nghiệm phức của phương trình \[{z^2} - 4z + 8 = 0\]. Giá trị của \[\left| {{z_1}} \right| + \left| {{z_2}} \right|\] bằng
Từ một tấm tôn dạng hình tròn với bán kính \[R = 50cm\], một anh thợ cần cắt một tấm tôn có dạng hình chữ nhật nội tiếp hình tròn trên. Anh ta gò tấm tôn hình chữ nhật này thành một hình trụ không đáy (như hình vẽ) để thả gà vào trong. Thể tích lớn nhất của khối trụ thu được gần nhất với kết quả nào dưới đây?
![Từ một tấm tôn dạng hình tròn với bán kính \[R = 50cm\], một anh thợ cần cắt một tấm tôn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/blobid13-1653317243.png)
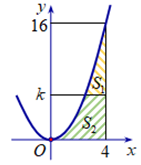
Cho hình phẳng \[\left( H \right)\] giới hạn bởi các đường \[y = {x^2},y = 0,x = 0,x = 4\]. Đường thẳng \[y = k\left( {0 < k < 16} \right)\] chia hình \[\left( H \right)\] thành hai phần có diện tích \[{S_1},{S_2}\] như hình vẽ. Tìm k để \[{S_1} = {S_2}\]
Trong không gian Oxyz, cho mặt phẳng . Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Cho hàm số \[f\left( x \right)\] có bảng biến thiên như sau:
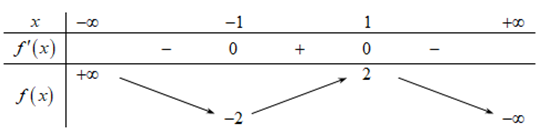
Phương trình \[f\left( x \right) - 2 = 0\] có số nghiệm thực là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh \[AB = a,SA = a\sqrt 3 \]và SA vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng \[\left( {SAC} \right)\] bằng
Tìm nguyên hàm của hàm số \[f\left( x \right) = \frac{{{{\ln }^3}x}}{x}\]
Cho cấp số cộng \[\left( {{u_n}} \right)\] với \[{u_2} = 6,{u_5} = 21\]. Tính d.
Trong không gian Oxyz, hình chiếu vuông góc của điểm \[M\left( {1;2; - 3} \right)\] trên trục Oy có tọa độ là
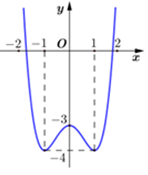
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
Tập nghiệm của phương trình \[{2^{{x^2} - 3x + 6}} = {2^{x + 3}}\] là