Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy là \(SA = \sqrt 2 a\). Tính thể tích V của khối chóp S.ABCD.

Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \frac{{x + 3}}{{x + 4m}}\) nghịch biến trên khoảng \(\left( {12; + \infty } \right)\)?

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{e^x} + 1} \right)\left( {{e^x} - 12} \right)\left( {x + 1} \right){\left( {x - 1} \right)^2}\) trên \(\mathbb{R}\). Hỏi hàm số có bao nhiêu điểm cực trị?

Cho \(b,c \in \mathbb{R}\) và phương trình \({z^2} + b{\rm{z}} + c = 0\) có một nghiệm là \({z_1} = 2 - i\), nghiệm còn lại gọi là \({z_2}\). Tính số phức \[{\rm{w}} = b{{\rm{z}}_1} + c{{\rm{z}}_2}\].

Cho số phức z, biết rằng các điểm biểu diễn hình học của các số phức z, iz và \(z + iz\) tạo thành một tam giác có diện tích bằng 18. Tập hợp điểm biểu diễn hình học của số phức \[{\rm{w}} = \left( {1 + i} \right)z - 2\] là một đường tròn có bán kính bằng

Cho số phức z thỏa mãn \(z\left( {3 + 2i} \right) + 14i = 5\) . Tìm môđun của số phức z.

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ.

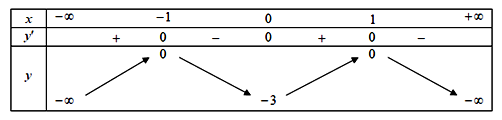
Hàm số \(y = f\left( x \right)\) làm hàm số nào trong các hàm số sau?

Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con xúc sắc đó không vượt quá 5 bằng

Cho phương trình \(\log _3^2\left( {3{\rm{x}}} \right) - \left( {m + 2} \right){\log _3}x + m - 2 = 0\) (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn \(\left[ {\frac{1}{3};3} \right]\) là

Cho hàm số \(f\left( x \right) = {x^3} - 3{{\rm{x}}^2}\). Số giá trị nguyên của m để phương trình \(f\left( {{x^4} - 4{{\rm{x}}^2} + 2} \right) = m\) (1) có đúng 4 nghiệm phân biệt là

Gọi \(\left( S \right)\) là mặt cầu đi qua 4 điểm \(A\left( {2;0;0} \right),B\left( {1;3;0} \right),C\left( { - 1;0;3} \right),D\left( {1;2;3} \right)\). Tính bán kính R của \(\left( S \right)\).

Cho hai hình trụ có bán kính đường tròn đáy lần lượt là \({R_1},{R_2}\) và chiều cao lần lượt là \({h_1},{h_2}\). Nếu hai hình trụ có cùng thể tích và \(\frac{{{h_1}}}{{{h_2}}} = \frac{9}{4}\) thì tỉ số \(\frac{{{R_1}}}{{{R_2}}}\) bằng

Cho hình chóp S.ABC có \(AB = 3\). Hình chiều của S lên mặt phẳng \(\left( {ABC} \right)\) là điểm H thuộc miền trong tam giác ABC sao cho \(\widehat {AHB} = 120^\circ \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.HAB, biết \(SH = 4\sqrt 3 \).

Trong không gian tọa độ Oxyz, mặt phẳng chứa trục Oz và đi qua điểm \(I\left( {1;2;3} \right)\) có phương trình là

Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

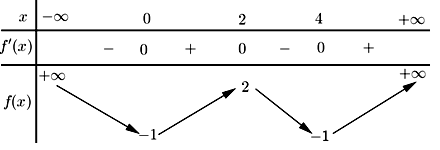
Số nghiệm thuộc khoảng \(\left( {0;\pi } \right)\) của phương trình \(3f\left( {2 + 2\cos x} \right) - 4 = 0\) là

Cho phương trình \({\log _5}\left( {x + y} \right) + 2{{\rm{x}}^2} + {y^2} + 3{\rm{x}}y - 11{\rm{x}} - 6y + 4 = 0\). Hỏi có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên dương thỏa mãn phương trình trên.