Cho 3 số thực a, b, c thỏa mãn \({\log _2}\frac{{a + b + c}}{{{a^2} + {b^2} + {c^2} + 2}} = a\left( {a - 4} \right) + b\left( {b - 4} \right) + c\left( {c - 4} \right)\). Giá trị lớn nhất của biểu thức \(P = \frac{{a + 2b + 3c}}{{a + b + c}}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Biến đổi giả thiết ta có: \({\log _2}\frac{{a + b + c}}{{{a^2} + {b^2} + {c^2} + 2}} = a\left( {a - 4} \right) + b\left( {b - 4} \right) + c\left( {c - 4} \right)\)
\( \Leftrightarrow {\log _2}\left( {a + b + c} \right) + 2 + 4\left( {a + b + c} \right) = {\log _2}\left( {{a^2} + {b^2} + {c^2} + 2} \right) + {a^2} + {b^2} + {c^2} + 2\)
\( \Leftrightarrow {\log _2}4\left( {a + b + c} \right) + 4\left( {a + b + c} \right) = {\log _2}\left( {{a^2} + {b^2} + {c^2} + 2} \right) + {a^2} + {b^2} + {c^2} + 2\)
Xét hàm số \(f\left( t \right) = {\log _2}t + t\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Khi đó \(f\left[ {4\left( {a + b + c} \right)} \right] = f\left( {{a^2} + {b^2} + {c^2} + 2} \right) \Leftrightarrow 4\left( {a + b + c} \right) = {a^2} + {b^2} + {c^2} + 2\)
\( \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} = 10\) \(\left( S \right)\)
Điểm \(M\left( {a;b;c} \right)\)thuộc mặt cầu \(\left( S \right)\): \({\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 2} \right)^2} = 10\)
Mặt khác \(P = \frac{{a + 2b + 3c}}{{a + b + c}} \Leftrightarrow a\left( {P - 1} \right) + b\left( {P - 2} \right) + c\left( {P - 3} \right) = 0\) \(\left( P \right)\)
Điều kiện để \(\left( P \right)\) và \(\left( S \right)\) có giao điểm là \(d\left( {I;\left( P \right)} \right) \le R\left( {I\left( {2;2;2} \right);R = \sqrt {10} } \right) \Leftrightarrow \frac{{\left| {6P - 12} \right|}}{{\sqrt {3{P^2} - 12P + 14} }} \le \sqrt {10} \)
\( \Leftrightarrow P \le \frac{{6 + \sqrt {30} }}{3}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hàm số \(f\left( x \right) = {\log _3}\left( {{x^2} - 4x} \right)\) có đạo hàm trên miền xác định là \(f'\left( x \right)\). Chọn kết quả đúng.
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\left[ {0;2} \right]\) thỏa mãn \(f\left( 2 \right) = 1\), \(\int\limits_0^2 {{{\left[ {f'\left( x \right)} \right]}^2}} dx = \frac{2}{7}\) và \(\int\limits_0^2 {{x^2}.f\left( x \right)} dx = \frac{{40}}{{21}}\). Tính tích phân \(I = \int\limits_0^2 {f\left( x \right)dx} \).
Số nghiệm thực của phương trình \(2{\log _2}\left( {x - 3} \right) = 2 + {\log _{\sqrt 2 }}\sqrt {3 - 2x} \) là
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên:
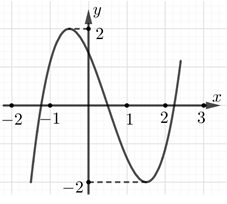
Số nghiệm thực của phương trình \(f\left( {\left| {f\left( x \right)} \right|} \right) = 0\) là
Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn \(\left[ {2;4} \right]\)
Cho một hộp đựng 12 viên bi, trong đó có 7 viên bi đỏ, 5 viên bi xanh. Lấy ngẫu nhiên một lần 3 viên bi. Tính xác xuất lấy được ít nhất 2 viên bi màu xanh.
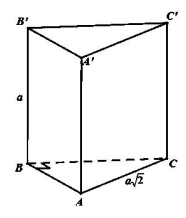
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có \(BB' = a\), đáy ABC là tam giác vuông cân tại B, \(AC = a\sqrt 2 \). Tính thể tích lăng trụ
Nếu cấp số nhân \(\left( {{u_n}} \right)\) có công bội q và \({u_1} = \frac{1}{2}\), \({u_5} = 8\) thì
Phương trình \[{9^x} - {3^{x + 1}} + 2 = 0\] có hai nghiệm \[{x_1}\]; \({x_2}\) với \({x_1} < {x_2}\). Đặt \(P = 2{x_1} + 3{x_2}\). Khi đó:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, \(AB = BC = a\), \(AD = 2a\). Tam giác SAD đều và nằm trong mặt phẳng vuông góc với đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABC theo a.
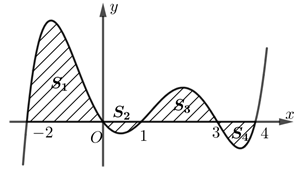
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị tạo với trục hoành các miền có diện tích là \({S_1}\), \({S_2}\), \({S_3}\), \({S_4}\) như hình vẽ. Biết \({S_1} = 6\), \({S_2} = 1\), \({S_3} = 4\), \({S_4} = 2\) tích phân \(I = \int\limits_0^{\ln 2} {{e^x}f\left( {3{e^x} - 2} \right)dx} \) bằng
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính thể tích của khối chóp S.ABCD theo a.
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
|
x |
\( - \infty \) |
|
1 |
|
2 |
|
4 |
|
\( + \infty \) |
|
\(f'\left( x \right)\) |
|
+ |
0 |
+ |
0 |
– |
0 |
+ |
|
Số điểm cực trị của hàm số \(y = - 2f\left( x \right)\) là
Cho hàm số \[y = f\left( x \right) = {x^3} - 3{x^2} + 2\]có đồ thị như hình 1
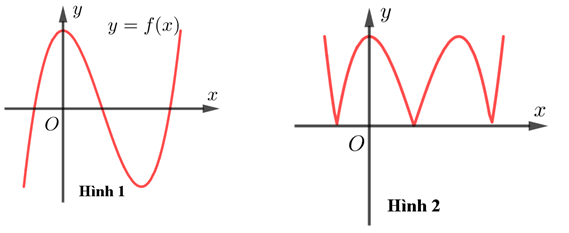
Hình 2 là đồ thị của hàm số nào trong các hàm số sau đây?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
|
x |
\( - \infty \) |
|
1 |
|
3 |
|
\( + \infty \) |
|
\(y'\) |
|
+ |
0 |
– |
0 |
+ |
|
|
y |
\( - \infty \) |
|
4 |
|
–2 |
|
\( + \infty \) |
Tìm tất cả các giá trị của m để bất phương trình \(f\left( {\sqrt {x - 1} + 1} \right) \le m\) có nghiệm?