Bất phương trình \[{4^x} - \left( {m + 1} \right){2^{x + 1}} + m \ge 0\] nghiệm đúng với mọi \[x \ge 0\]. Tập tất cả các giá trị của m là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Đặt \(t = {2^x}\). Với \(x \ge 0\) thì \(t \ge 1.\)
Bất phương trình đã cho trở thành: \({t^2} - 2\left( {m - 1} \right)t + m \ge 0\left( * \right)\).
Bài toán trở thành: Tìm m để bất phương trình (*) nghiệm đúng với mọi \(t \ge 1.\)
Ta có: \(\left( * \right) \Leftrightarrow {t^2} - 2t \ge m\left( {2t - 1} \right) \Leftrightarrow m \le \frac{{{t^2} - 2t}}{{2t - 1}}\) (Do \(t \ge 1\)).
Xét hàm số: \(f\left( t \right) = \frac{{{t^2} - 2t}}{{2t - 1}}\) trên \(\left[ {1; + \infty } \right)\) có đạo hàm \(f'\left( t \right) = \frac{{2{t^2} - 2t + 2}}{{{{\left( {2t - 1} \right)}^2}}} > 0\) với mọi \(t \ge 1.\)
Hàm số đồng biến dẫn đến \(\mathop {Min}\limits_{\left[ {1; + \infty } \right)} f\left( t \right) = - 1.\)
Do đó để bất phương trình (*) nghiệm đúng với mọi \(t \ge 1\) thì \(m \le \mathop {Min}\limits_{\left[ {1; + \infty } \right)} f\left( t \right) = - 1.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phương trình \[{\log _3}^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0\]. Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc \[\left[ {1;81} \right]\] là
Cho \[\int\limits_0^3 {f\left( x \right)dx} = 2\]. Tính giá trị của tích phân \[L = \int\limits_0^3 {\left[ {2f\left( x \right) - {x^2}} \right]dx} \].
Kí hiệu \[{z_1},{z_2},{z_3},{z_4}\] là bốn nghiệm phức của phương trình \[{z^4} + 3{z^2} - 4 = 0.\] Tính tổng \[T = \left| {{z_1}} \right| + {\left| z \right|_2} + \left| {{z_3}} \right| + \left| {{z_4}} \right|.\]
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \[{d_1}:\;\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{3} = \frac{{z - 1}}{2}\] và \[{d_2}:\;\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\\z = - 1 - t\end{array} \right..\] Phương trình đường thẳng \[\Delta \] nằm trong mặt phẳng \[\left( P \right):\;x + 2y - 3z - 2 = 0\] cắt cả hai đường thẳng \[{d_1}\] và \[{d_2}\] là
Biết \[\int\limits_4^5 {\frac{{dx}}{{{x^2} + 3x + 2}} = a\ln 2 + b\ln 3 + c\ln 5 + d\ln 7} \] với \[a,b,c,d\] là các số nguyên. Tính \[P = ab + cd.\]
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \[B,AB = 3a,BC = 4a\]. Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo bởi giữa SC và mặt phẳng đáy bằng \[{60^0}\]. Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
Cho hàm số \[f\left( x \right) = 2x + {e^x}\]. Tìm một nguyên hàm \[F\left( x \right)\] của hàm số f(x) thỏa mãn \[F\left( 0 \right) = 2019\].
Cho cấp số cộng có \[{u_1} = - 3;{u_{10}} = 24\]. Tìm công sai d?
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \[x = 1\] và \[x = 4\], biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\] (\[1 \le x \le 4\]) thì được thiết diện là một hình lục giác đều có độ dài cạnh là \[2x\].
Có bao nhiêu số phức z thỏa mãn \[\left| {z - 2 + i} \right| = \left| {z + 1 - 2i} \right|\] và \[\left| {z + 4 - 2i} \right| = 3\sqrt 2 ?\]
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \[\left( P \right):x - 2y + 2z - 2 = 0\] và điểm \[I\left( { - 1;2; - 1} \right)\]. Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5.
Cho hàm số f(x) liên tục trên \[\left[ {0;{\mkern 1mu} 1} \right].\] Biết \[\int\limits_0^1 {\left[ {x.{\mkern 1mu} f'\left( {1 - x} \right) - f\left( x \right)} \right]{\mkern 1mu} {\rm{d}}x} = \frac{1}{2},\] tính \[f\left( 0 \right).\]
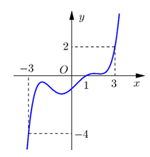
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đồ thị \[y = f'\left( x \right)\] như hình vẽ. Đặt \[g\left( x \right) = 2f\left( x \right) - {\left( {x - 1} \right)^2}.\] Khi đó giá trị nhỏ nhất của hàm số \[y = g\left( x \right)\] trên đoạn \[\left[ { - 3;3} \right]\] bằng