Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 23)
-
6362 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P):2x−y+z+4=0. Khi đó mặt phẳng (P) có một vectơ pháp tuyến là
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
Mặt phẳng (P):ax+by+cz+d=0 có một vectơ pháp tuyến →n=(a;b;c)
Cách giải
Mặt phẳng (P):2x−y+z+4=0 có một VTPT là →n=(2;−1;1).Câu 2:
Cho a là số thực dương bất kì khác 1. Tính S=loga(a34√a).
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức logaan=n.
Cách giải
Ta có: S=loga(a34√a)=loga(a3.a14)=loga134=134.
Câu 3:
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên (a;b) có y′>0 với x∈(a;b) thì hàm số đồng biến trên (a;b).
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng (−∞;−1) và (0;1).
Câu 4:
Cho phương trình 22x−5.2x+6=0 có hai nghiệm x1,x2. Tính P=x1.x2.
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Coi phương trình đã cho là bậc hai ẩn 2x, giải phương trình tìm x và kết luận.
Cách giải
Ta có: 22x−5.2x+6=0⇔(2x−2)(2x−3)=0⇔[2x=22x=3⇔[x=1x=log23
Do đó P=x1x2=1.log23=log23.
Câu 5:
Cho cấp số cộng có u1=−3;u10=24. Tìm công sai d?
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Sử dụng công thức: Cho cấp số cộng có số hạng đầu u1 và công sai d thì số hạng thứ n(n>1) là
un=u1+(n−1)d.
Từ đó ta tìm được công sai d.
Cách giải
Ta có u10=u1+9d⇔−3+9d=24⇔9d=27⇔d=3.
Câu 6:
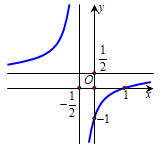
Đồ thị trong hình bên là của hàm số nào sau đây:
 Xem đáp án
Xem đáp án
Đáp án D
Nhìn vào đồ thị ta thấy đồ thị hàm số có tiệm cận đứng x=−12, tiệm cận ngang y=12.
Đồ thị đi qua (1;0) và (0;−1).
Phương án A có tiệm cận đứng x=12 suy ra loại phương án A.
Phương án B có tiệm cận đứng x=12 suy ra loại phương án B.
Phương án C cắt trục hoành tại (−1;0) suy ra loại phương án C.
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho →a=→i+3→j−2→k. Tọa độ của vectơ →a là
 Xem đáp án
Xem đáp án
Đáp án D
Ta có →a=(1;3;−2)
Câu 8:
Hình nón có diện tích xung quanh bằng 24π và bán kính đường tròn đáy bằng 3. Đường sinh của hình nón có độ dài bằng:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng công thức tính diện tích xung quanh hình nón Sxq=πrl (với r là bán kính đáy, l là đường sinh hình nón).
Cách giải
Ta có diện tích xung quanh hình nón bằng Sxq=πrl⇔l=Sxqπr=24ππ.3=8.
Câu 9:
Một đa giác lồi có 50 cạnh thì có bao nhiêu đường chéo.
 Xem đáp án
Xem đáp án
Đáp án C
Chọn 2 điểm tùy ý không liền nhau, nối lại ta được 1 đường chéo thỏa mãn.
Chọn 2 điểm tùy ý từ 50 điểm có C250 cách, ứng với C250 đoạn thẳng.
Trong C250 đoạn thẳng này thì có đúng 50 cạnh của đa giác đã cho, còn lại là các đường chéo.
Vậy có tất cả C250−50 đường chéo.
Câu 10:
Trong không gian Oxyz, cho điểm A(−4;0;1) và mặt phẳng (P):x−2y−z+4=0. Mặt phẳng (Q) đi qua điểm A và song song với mặt phẳng (P) có phương trình là
 Xem đáp án
Xem đáp án
Đáp án D
Cách giải
(P):x−2y−z+4=0 có VTPT →nP=(1;−2;−1) nên (Q)//(P)⇒→nQ=(1;−2;−1).
(Q) đi qua A(−4;0;1) và nhận →nQ=(1;−2;−1) làm VTPT nên (Q) có phương trình là:
1(x+4)−2(y−0)−1(z−1)=0⇔x−2y−z+5=0.
Chú ý khi giải: Các em có thể loại dần các đáp án bằng việc kiể tra VTPT của (Q) và thay tọa độ điểm A vào các phương trình chưa bị loại để kiểm tra.
Câu 11:
Cho hàm số f(x)=2x+ex. Tìm một nguyên hàm F(x) của hàm số f(x) thỏa mãn F(0)=2019.
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
- Tìm nguyên hàm của hàm số.
- Thay điểm kiện bài cho tìm hằng số C.
Cách giải
Ta có: F(x)=∫(2x+ex)dx=x2+ex+C.
Do F(0)=2019 nên 02+e0+C=2019⇔C=2018.
Vậy F(x)=x2+ex+2018.
Câu 12:
Gọi V là thể tích của hình lập phương ABCD.A′B′C′D′, V1 là thể tích tứ diện A′ABD. Hệ thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án C
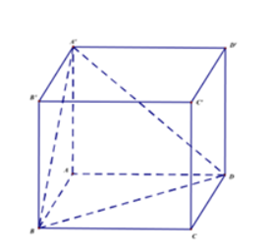
Gọi a là cạnh của hình lập phương
Khi đó, ta có: V=a3 và V1=13.12a2.a=a36
Vậy V=6V1
Câu 13:
Tìm số phức liên hợp của số phức z thỏa mãn (1−i)z=1+3i.
 Xem đáp án
Xem đáp án
Đáp án C
z=1+3i1−i=(1+3i)(1+i)2=−1+2i⇒¯z=−1−2i.
Câu 14:
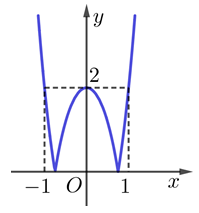
Cho hàm số y=f(x) có đồ thị như hình vẽ. Trên khoảng (−1;1) đồ thị hàm số có mấy điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án D
Đồ thị hàm số có 3 điểm cực trị trên khoảng (−1;1).
Câu 15:
Cho 3∫0f(x)dx=2. Tính giá trị của tích phân L=3∫0[2f(x)−x2]dx.
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Sử dụng các tính chất tích phân b∫a[f(x)±g(x)]dx=b∫af(x)dx±b∫ag(x)dx và b∫akf(x)dx=kb∫af(x)dx.
Cách giải
Ta có: L=3∫0[2f(x)−x2]dx=3∫02f(x)dx−3∫0x2dx=23∫0f(x)dx−x33|30=2.2−333=−5.
Câu 16:
thị của hàm số y=−x3+3x2+2x−1 và đồ thị hàm số y=3x2−2x−1 có tất cả bao nhiêu điểm chung:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Số nghiệm của hai đồ thị hàm số là số giao điểm của phương trình hoành độ giao điểm của hai đồ thị.
Giải phương trình hoành độ giao điểm của hai đồ thị hàm số.
Cách giải
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
−x3+3x2+2x−1=3x2−2x−1
⇔x3−4x=0⇔[x=0x=−2x=2
⇒ Hai đồ thị hàm số có 3 điểm chung.
Câu 17:
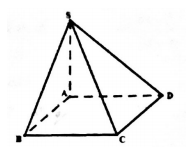
Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy, mặt bên (SBC) tạo với đáy một góc 300.Thể tích của khối chóp đã cho bằng
 Xem đáp án
Xem đáp án
Đáp án B
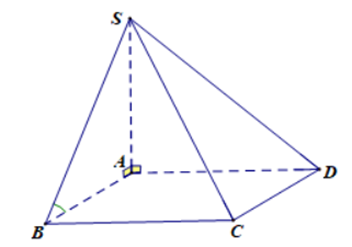
Ta có: {(SBC)∩(ABCD)=BCAB⊥BCSB⊥BC⇒ Góc giữa (SBC) và đáy là ^SBA=30∘.
Lại có: SA=AB.tan30∘=2a√33. Vậy: VS.ABCD=13.SA.SABCD=13.2a√33.4a2=8a3√39.
Câu 18:
Kí hiệu z1,z2,z3,z4 là bốn nghiệm phức của phương trình z4+3z2−4=0. Tính tổng T=|z1|+|z|2+|z3|+|z4|.
 Xem đáp án
Xem đáp án
Đáp án C
Ta có z4+3z2−4=0⇒[z2=1z2=−4=4i2⇒[z=±1z=±2i
⇒T=|1|+|−1|+|2i|+|−2i|=6.
Câu 19:
Tính đạo hàm của hàm số y=(x2+4x+3)e2x ?
 Xem đáp án
Xem đáp án
Đáp án C
y′=(2x+4).e2x+2e2x(x2+4x+3)=(2x2+10x+10)e2x.
Câu 20:
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2x3−3x2−12x+10 trên đoạn [−3;3] là:
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp
- Tính y′ và tìm nghiệm của y′=0 trên đoạn [−3;3].
- Tính giá trị của hàm số tại hai điểm −3;3 và các điể là nghiệm của đạo hàm ở trên.
- So sánh kết quả và kết luận.
Cách giải
Ta có: y′=6x2−6x−12=0⇔[x=−1∈[−3;3]x=2∈[−3;3]
Lại có: y(−3)=−35,y(−1)=17,y(2)=−10,y(3)=1.
Do đó giá trị lớn nhất của hàm số trên [−3;3] là M=17 và giá trị nhỏ nhất của hàm số trên [−3;3] là m=−35;
Vậy T=M+m=17+(−35)=−18.
Câu 21:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x−2y+2z−2=0 và điểm I(−1;2;−1). Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5.
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ R2=h2+r2 với h=d(I,(P)). Từ đó ta tính được R.
+ Phương trình mặt cầu tâm I(x0;y0;z0) và bán kính R có dạng (x−x0)2+(y−y0)2+(z−z0)2=R2
Cách giải
+ Ta có h=d(I,(P))=|−1−2.2+2.(−1)−2|√12+(−2)2+22=93=3.
+ Từ đề bài ta có bán kính đường tròn giao tuyến là r=5 nên bán kính mặt cầu là R=√r2+h2=√52+32=√34.
+ Phương trình mặt cầu tâm I(−1;2;−1) và bán kính R=√34 là (x+1)2+(y−2)2+(z+1)2=34.
Câu 22:
Cho hình chóp S.ABCD đều có AB=2 và SA=3√2. Bán kính của mặt cầu ngoại tiếp hình chóp đã cho bằng
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.
Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều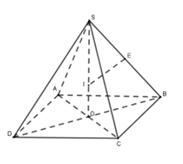
Cách giải
Gọi O là tâm hình vuông ABCD và E là trung điểm SB.
Vì S.ABCD là hình chóp đều nên SO⊥(ABCD).
Trong (SBO) kẻ đường trung trực của SB cắt SO tại I, khi đó IA=IB=IC=ID=IS nên I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD và bán kính mặt cầu là R=IS.
Ta có ABCD là hình vuông cạnh 2
⇒BD=√BC2+CD2=2√2⇒BO=BD2=√2.
Ta có SA=SB=SC=SD=3√2 (vì S.ABCD là hình chóp đều) nên SE=EB=3√22
Xét tam giác SBO vuông tại O (vì SO⊥(ABCD)⇒SO⊥OB) có \(SO = \sqrt {S{B^2} - O{B^2}} = \sqrt {18 - 2} = 4.\)
Ta có ΔSEI đồng dạng với tam giác SOB (g−g)⇒SISB=SESO⇔IS=SB.SESO=3√2.3√224=94.
Vậy bán kính R=94.
Chú ý: Các em có thể sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp đều có cạnh bên là a và chiều cao h là R=a22h.
Câu 23:
Cho hàm số y=f(x) xác định trên R và có đạo hàm f′(x)=x(x−1)3(x+2)5. Số điểm cực tiểu của hàm số đã cho là
 Xem đáp án
Xem đáp án
Đáp án B
Ta có f′(x)=0⇔[x=0x=1x=−2
Xét bảng sau:
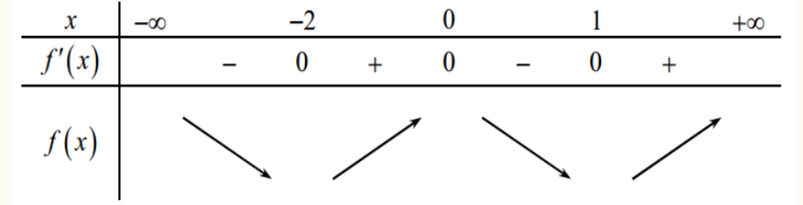
Hàm số đạt cực tiểu tại x=−2;x=1.
Câu 24:
Cho log27|a|+log9b2=5 và log27|b|+log9a2=7. Giá trị của |a|−|b| bằng
 Xem đáp án
Xem đáp án
Đáp án D
Ta có hệ {13log3|a|+log3|b|=5log3|a|+13log3|b|=7⇔{|a|=729|b|=27
Vậy |a|−|b|=702
Câu 25:
Hệ số x5 trong khai triển của đa thức f(x)=x(1−x)10+x2(1+2x)5 bằng :
 Xem đáp án
Xem đáp án
Đáp án B
Cần tìm hệ số của x4 trong khai triển nhị thức thứ nhất và hệ số của x3 trong khai triển nhị thức thứ hai. Hệ số của x5 là C410+23C35=290.
Câu 26:
Biết bất phương trình log5(5x−1).log25(5x+1−5)≤1 có tập nghiệm là đoạn [a;b]. Giá trị của a+b bằng
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Giải bất phương trình bằng cách đưa về bất phương trình bậc hai, ẩn là log5(5x−1).
Cách giải
Điều kiện: 5x−1>0⇔x>0
Ta có:
log5(5x−1).log25(5x+1−5)≤1⇔log5(5x−1).12log5[5(5x−1)]≤1
⇔log5(5x−1).[1+log5(5x−1)]−2≤0
⇔log25[5x−1]+log5(5x−1)−2≤0
⇔[log5(5x−1)−1][log5(5x−1)+2]≤0
⇔−2≤log5(5x−1)≤1⇔5−2≤5x−1≤51⇔125≤5x−1≤5
⇔2625≤5x≤6⇔log52625≤x≤log56
Do đó tập nghiệm của bất phương trình là [log52625;log56]⇒a=log52625;b=log56.
⇒a+b=log52625+log56=log515625=log5156−log525=log5156−2
Câu 27:
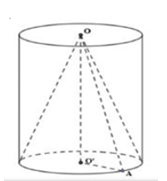
Một hình trụ có hai đáy là hai hình tròn (O;x) và (O′;x). Khoảng cách giữa hai đáy là OO′=r√3. Một hình nón có đỉnh O và có đáy là hình tròn (O′;x). Gọi S1 là diện tích xung quanh của hình trụ và S2 là diện tích xung quanh của hình nón. Tính tỉ số S1S2.
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp
Diện tích xung quanh của hình trụ: Sxq=2πrl=2πrh
Diện tích xung quanh của hình nón: Sxq=πrl.
Cách giải
Diện tích xung quanh của hình trụ: S1=2πrh=2πr.r√3=2π√3r2
ΔOO′A vuông tại O′⇒OA=√OO′2+O′A2=√3r2+r2=2r
Diện tích xung quanh của hình nón: Sxq=πrl=πr.2r=2πr2⇒S1S2=√3Câu 28:
Cho hàm số y=f(x) có bảng biến thiên như sau:

Số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho bằng:
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp
Cho hàm số y=f(x).
+) Nếu limx→∞y=y0⇒y=y0 là TCN của đồ thị hàm số.
+) Nếu \mathop {\lim }\limits_{x \to {x_0}} y = \infty \Rightarrow x = {x_0} là TCĐ của đồ thị hàm số.
Cách giải
Dựa vào BBT ta thấy:
\mathop {\lim }\limits_{x \to - \infty } y = 5 \Rightarrow y = 5 là TCN của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \Rightarrow x = 2\) là TCĐ của đồ thị hàm số.
\mathop {\lim }\limits_{x \to {3^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {3^ + }} y = + \infty \Rightarrow x = 3 TCĐ của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Câu 29:
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (1 \le x \le 4) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
- Tính diện tích thiết diện theo x.
- Tính thể tích theo công thức V = \int\limits_a^b {S\left( x \right)dx} .
Cách giải
Diện tích một tam giác đều cạnh 2x là \frac{{{{\left( {2x} \right)}^2}\sqrt 3 }}{4} = {x^2}\sqrt 3 .
Diện tích hình lục giác đều bằng 6 lần diện tích một tam giác đều nên S\left( x \right) = 6{x^2}\sqrt 3 .
Thể tích V = \int\limits_1^4 {S\left( x \right)dx} = \int\limits_1^4 {6{x^2}\sqrt 3 dx} = 2{x^3}\sqrt 3 \left| {_{\scriptstyle\atop\scriptstyle1}^{\scriptstyle4\atop\scriptstyle}} \right. = 126\sqrt 3 .
Chú ý khi giải: Nhiều em có thể sẽ nhớ nhầm công thức thành V = \pi \int\limits_a^b {S\left( x \right)} dx dẫn đến chọn nhầm đáp án A là sai.
Câu 30:
Trong không gian toạ độ Oxyz, cho hai đường thẳng {d_1} và {d_2} có phương trình là {d_1}:\frac{{x - 2}}{1} = \frac{{y - 1}}{1} = \frac{{z + 4}}{{ - 4}} và {d_2}:\frac{{x + 1}}{2} = \frac{{y + 1}}{2} = \frac{{z - 5}}{{ - 8}}. Viết phương trình mặt phẳng chứa đường thẳng {d_1} và {d_2}.
 Xem đáp án
Xem đáp án
Đáp án B
Câu 31:
Tìm nguyên hàm I = \int {\frac{x}{{\sqrt {2x + 1} }}dx} .
 Xem đáp án
Xem đáp án
Đáp án A
Đặt \sqrt {2x + 1} = t \Rightarrow x = \frac{{{t^2} - 1}}{2} \Rightarrow I = \int {\frac{{\frac{{{t^2} - 1}}{2}}}{t}d\left( {\frac{{{t^2} - 1}}{2}} \right) = \int {\frac{{{t^2} - 1}}{{2t}}.tdt} = \frac{1}{2}\int {\left( {{t^2} - 1} \right)dt} }
= \frac{1}{2}\left( {\frac{{{t^3}}}{3} - t} \right) + C = \frac{{{t^3}}}{6} - \frac{t}{2} + C = \frac{1}{6}\sqrt {{{\left( {2x + 1} \right)}^3}} - \frac{1}{2}\sqrt {2x + 1} + C.
Câu 32:
Biết \int\limits_4^5 {\frac{{dx}}{{{x^2} + 3x + 2}} = a\ln 2 + b\ln 3 + c\ln 5 + d\ln 7} với a,b,c,d là các số nguyên. Tính P = ab + cd.
 Xem đáp án
Xem đáp án
Đáp án B
Ta có \int\limits_4^5 {\frac{{dx}}{{{x^2} + 3x + 2}} = \int\limits_4^5 {\left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx} = \ln \left| {\frac{{x + 1}}{{x + 2}}} \right|\left| {_{\scriptstyle\atop\scriptstyle4}^{\scriptstyle5\atop\scriptstyle}} \right. = 2\ln 2 + 2\ln 3 - \ln 5 - \ln 7.}
Suy ra \left\{ \begin{array}{l}a = b = 2\\c = d = - 1\end{array} \right. \Rightarrow P = ab + cd = 5.
Câu 33:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng {d_1}:\;\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{3} = \frac{{z - 1}}{2} và {d_2}:\;\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\\z = - 1 - t\end{array} \right.. Phương trình đường thẳng \Delta nằm trong mặt phẳng \left( P \right):\;x + 2y - 3z - 2 = 0 cắt cả hai đường thẳng {d_1} và {d_2} là
 Xem đáp án
Xem đáp án
Đáp án C
Gọi A là giao điểm của {d_1} và \left( P \right),B là giao điểm của {d_2} và \left( P \right).
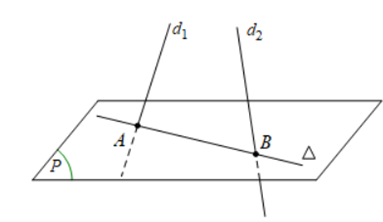
Ta có: A\left( {2 - a;1 + 3a;1 + 2a} \right) \in {d_1}, cho điểm A thuộc \left( P \right) thì
2 - a + 2\left( {1 + 3a} \right) - 3\left( {1 + 2a} \right) - 2 = 0
\Leftrightarrow - 1 - a = 0 \Leftrightarrow a = - 1 \Rightarrow A\left( {3; - 2; - 1} \right)
Điểm B\left( {1 - 3b; - 2 + b; - 1 - b} \right) \in {d_2}, cho B thuộc \left( P \right) thì 1 - 3b + 2\left( { - 2 + b} \right) + 3 + 3b - 2 = 0
\Leftrightarrow 2b - 2 = 0 \Leftrightarrow b = 1 \Rightarrow B\left( { - 2; - 1; - 2} \right)
Đường thẳng cần tìm là AB, vectơ chỉ phương của AB là \overrightarrow u = \overrightarrow {AB} \left( { - 5;1; - 1} \right).
Vậy \Delta :\frac{{x - 3}}{{ - 5}} = \frac{{y + 2}}{1} = \frac{{z + 1}}{{ - 1}}.
Câu 34:
Có bao nhiêu số phức z thỏa mãn \left| {z - 2 + i} \right| = \left| {z + 1 - 2i} \right| và \left| {z + 4 - 2i} \right| = 3\sqrt 2 ?
 Xem đáp án
Xem đáp án
Đáp án B
Đặt z = x + yi\left( {x,y \in \mathbb{R}} \right) từ giả thiết ta có: \left\{ \begin{array}{l}{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2}\\{\left( {x + 4} \right)^2} + {\left( {y - 2} \right)^2} = 18\end{array} \right.
\Leftrightarrow \left\{ \begin{array}{l}x = y\\{\left( {x + 4} \right)^2} + {\left( {y - 2} \right)^2} = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y\\2{x^2} + 4x + 2 = 0\end{array} \right. \Leftrightarrow x = y = - 1.
Vậy z = - 1 - i.
Câu 35:
Cho hàm số y = f\left( x \right) có bảng biến thiên như hình vẽ.
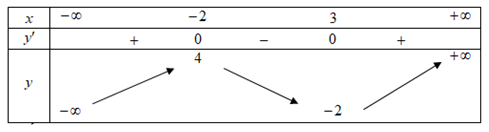
Hàm số g\left( x \right) = f\left( {2{x^2} - \frac{5}{2}x - \frac{3}{2}} \right) nghịch biến trên khoảng nào trong các khoảng sau?
 Xem đáp án
Xem đáp án
Đáp án C
Chọn f'\left( x \right) = k\left( {x + 2} \right)\left( {x - 3} \right) với k > 0
Khi đó g\left( x \right) = f\left( {2{x^2} - \frac{5}{2}x - \frac{3}{2}} \right) \Rightarrow g'\left( x \right) = k\left( {3x - \frac{5}{2}} \right)\left( {2{x^2} - \frac{5}{2}x + \frac{1}{2}} \right)\left( {2{x^2} - \frac{{5x}}{2} - \frac{9}{2}} \right)
Ta có bảng xét dấu
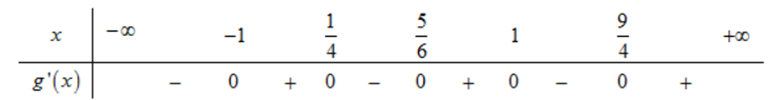
Do đó hàm số g\left( x \right) nghịch biến trên khoảng \left( {1;\frac{9}{4}} \right) nên hàm số nghịch biến trên khoảng \left( {1;\frac{5}{4}} \right).
Câu 36:
Thầy Tuấn có 15 cuốn sách gồm 4 cuốn sách Toán, 5 cuốn sách Lý, 6 cuốn sách Hóa. Các cuốn sách đôi một khác nhau. Thầy chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy Tuấn có đủ 3 môn:
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp
Tính xác suất của biến cố đối: P\left( A \right) = 1 - P\left( {\overline A } \right)
Cách giải
Số phần tử của không gian mẫu là: {n_\Omega } = C_{15}^8
Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: \overline A : “Số cuốn sách còn lại thầy Tuấn không có đủ cả 3 môn”.
Ta có các trường hợp xảy ra:
+) TH1: 7 cuốn sách còn lại chỉ có Toán và Lý. Số cách chọn là: C_9^7.
+) TH2: 7 cuốn sách còn lại chỉ có Lý và Hóa. Số cách chọn là: C_{11}^7.
+) TH3: 7 cuốn sách còn lại chỉ có Hóa và Toán. Số cách chọn là: 7C_{10}^7
\Rightarrow P\left( A \right) = 1 - P\left( {\overline A } \right) = \frac{{C_9^7 + C_{11}^7 + C_{10}^7}}{{C_{15}^8}} = 1 - \frac{{54}}{{715}} = \frac{{661}}{{715}}.
Câu 37:
Một công ty cần xây dựng một cái kho chứa hàng dạng hình hộp chữ nhật (có nắp) bằng vật liệu gạch và xi măng có thể tích 2000 {m^3}, đáy là hình chữ nhật có chiều dài bằng hai lần chiều rộng. Người ta cần tính toán sao cho chi phí xây dựng là thấp nhất, biết giá xây dựng là 500.000 đồng/{m^2}. Khi đó chi phí thấp nhất gần với số nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án D
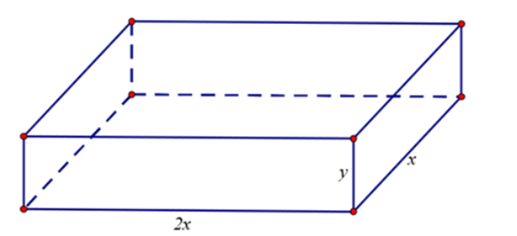
Gọi kích thước đáy của cái kho cần xây dựng là x\left( m \right) và 2x\left( m \right), chiều cao của kho là y\left( m \right), (với x,y > 0)
Ta có V = 2{x^2}y = 2000 \Rightarrow y = \frac{{1000}}{{{x^2}}}\left( m \right)
Diện tích toàn phần của hình hộp chữ nhật là
{S_{tp}} = 2\left( {x.2x + x.y + 2x.y} \right) = 4{x^2} + 6xy = 4{x^2} + \frac{{6000}}{x}
= 4{x^2} + \frac{{3000}}{x} + \frac{{3000}}{x} \ge 3\sqrt[x]{{4{x^2}.\frac{{3000}}{x}.\frac{{3000}}{x}}} = 300\sqrt[3]{{36}}\left( {{m^2}} \right)
Dấu đẳng thức xảy ra khi và chỉ khi 4{x^2} = \frac{{3000}}{x} \Leftrightarrow x = \sqrt[3]{{750}}\left( m \right)
Chi phí xây dựng thấp nhất khi đó sấp sỉ là 300\sqrt[3]{{36}}.500000 \approx 495289087 đồng
Câu 38:
Bất phương trình {4^x} - \left( {m + 1} \right){2^{x + 1}} + m \ge 0 nghiệm đúng với mọi x \ge 0. Tập tất cả các giá trị của m là
 Xem đáp án
Xem đáp án
Đáp án B
Đặt t = {2^x}. Với x \ge 0 thì t \ge 1.
Bất phương trình đã cho trở thành: {t^2} - 2\left( {m - 1} \right)t + m \ge 0\left( * \right).
Bài toán trở thành: Tìm m để bất phương trình (*) nghiệm đúng với mọi t \ge 1.
Ta có: \left( * \right) \Leftrightarrow {t^2} - 2t \ge m\left( {2t - 1} \right) \Leftrightarrow m \le \frac{{{t^2} - 2t}}{{2t - 1}} (Do t \ge 1).
Xét hàm số: f\left( t \right) = \frac{{{t^2} - 2t}}{{2t - 1}} trên \left[ {1; + \infty } \right) có đạo hàm f'\left( t \right) = \frac{{2{t^2} - 2t + 2}}{{{{\left( {2t - 1} \right)}^2}}} > 0 với mọi t \ge 1.
Hàm số đồng biến dẫn đến \mathop {Min}\limits_{\left[ {1; + \infty } \right)} f\left( t \right) = - 1.
Do đó để bất phương trình (*) nghiệm đúng với mọi t \ge 1 thì m \le \mathop {Min}\limits_{\left[ {1; + \infty } \right)} f\left( t \right) = - 1.
Câu 39:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,AB = 3a,BC = 4a. Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo bởi giữa SC và mặt phẳng đáy bằng {60^0}. Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
 Xem đáp án
Xem đáp án
Đáp án B
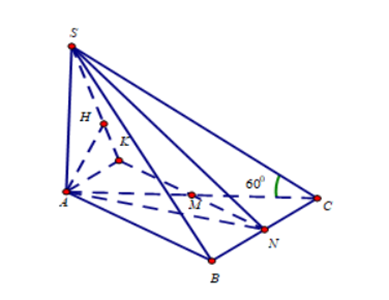
Gọi N là trung điểm của BC. Ta có: d\left( {AB;SM} \right) = d\left( {A;\left( {SMN} \right).} \right)
Dựng đường cao AK trong tam giác AMN, đường cao AH trong tam giác SAK.
Do SA \bot \left( {ABC} \right) nên SA \bot MN. (1)
Theo cách dựng ta lại có MN \bot AK. (2)
Từ (1) và (2) \Rightarrow MN \bot AH mà AH \bot SA (theo cách dựng).
\Rightarrow AH \bot \left( {SMN} \right) tại H nên d\left( {AB;SM} \right) = d\left( {A;\left( {SMN} \right)} \right) = AH.
Ta có: AK = BN = \frac{{BC}}{2} = 2a;AC = 5a.
Xét tam giác SAC có SA = AC.\tan 60^\circ = 5a\sqrt 3 .
Xét tam giác SAK vuông tại A với đường cao AH có:
\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{K^2}}} = \frac{1}{{75{a^2}}} + \frac{1}{{4{a^2}}} = \frac{{79}}{{300{a^2}}} \Rightarrow A{H^2} = \frac{{300{a^2}}}{{79}} \Rightarrow AH = \frac{{10\sqrt 3 a}}{{\sqrt {79} }}.
Câu 40:
Cho hàm số f(x) liên tục trên \left[ {0;{\mkern 1mu} 1} \right]. Biết \int\limits_0^1 {\left[ {x.{\mkern 1mu} f'\left( {1 - x} \right) - f\left( x \right)} \right]{\mkern 1mu} {\rm{d}}x} = \frac{1}{2}, tính f\left( 0 \right).
 Xem đáp án
Xem đáp án
Đáp án C
Ta có: I = \int\limits_0^1 {\left[ {x.f'\left( {1 - x} \right) - f\left( x \right)} \right]dx} = \int\limits_0^1 {x.f'\left( {1 - x} \right)dx} - \int\limits_0^1 {f\left( x \right)dx}
Đặt t = 1 - x \Rightarrow dt = - dx. Đổi cận \left| \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = 0\end{array} \right., ta có \int\limits_0^1 {x.f'\left( {1 - x} \right)dx = \int\limits_1^0 {\left( {1 - t} \right)f'\left( t \right)\left( { - dt} \right)} }
= \int\limits_0^1 {\left( {1 - x} \right)f'\left( x \right)dx}
Đặt \left\{ \begin{array}{l}u = 1 - x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = - dx\\v = f\left( x \right)\end{array} \right. ta có:
\int\limits_0^1 {\left( {1 - x} \right)f'\left( x \right)dx} = \left( {1 - x} \right)f\left( x \right)\left| {_{\scriptstyle\atop\scriptstyle0}^{\scriptstyle1\atop\scriptstyle}} \right. + \int\limits_0^1 {f\left( x \right)dx} = - f\left( 0 \right) + \int\limits_0^1 {f\left( x \right)dx}
Suy ra I = - f\left( 0 \right) \Rightarrow f\left( 0 \right) = - \frac{1}{2}.
Câu 41:
Trong không gian Oxyz, cho hai điểm A\left( {2; - 2;4} \right),B\left( { - 3;3; - 1} \right) và mặt cầu \left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 3. Xét điểm M thay đổi thuộc mặt cầu (S), giá trị nhỏ nhất của 2M{A^2} + 3M{B^2} bằng
 Xem đáp án
Xem đáp án
Đáp án C
Mặt cầu \left( S \right) có tâm J\left( {1;3;3} \right),R = \sqrt 3 .
Gọi I là điểm thỏa mãn 2\overrightarrow {IA} + 3\overrightarrow {IB} = \overrightarrow 0 \Rightarrow I\left( { - 1;1;1} \right) và \overrightarrow {IJ} = \left( {2;2;2} \right) \Rightarrow IJ = 2\sqrt 3 .
Khi đó P = 2M{A^2} + 3M{B^2} = 2{\left( {\overrightarrow {MA} } \right)^2} + 3{\left( {\overrightarrow {MB} } \right)^2} = 2{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + 3{\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2}
Suy ra P = 5M{I^2} + 2I{A^2} + 3I{B^2} + 2\overrightarrow {MI} \left( {\underbrace {2\overrightarrow {IA} + 3\overrightarrow {IB} }_{\overrightarrow 0 }} \right)
Do đó {P_{\min }} \Leftrightarrow M{I_{\min }}. Ta có hình minh họa sau:
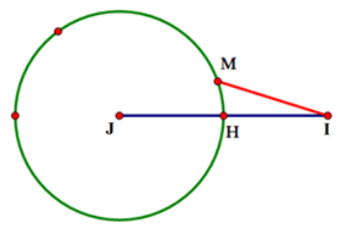
Khi đó M{I_{\min }} \Leftrightarrow MI = IH \Rightarrow I \equiv H với H là trung điểm IJ.
Khi đó ta có IM = \frac{{IJ}}{2} = \frac{{2\sqrt 3 }}{2} = \sqrt 3 . Đồng thời \left\{ \begin{array}{l}IA = 3\sqrt 3 \\IB = 2\sqrt 3 \end{array} \right.
Do đó {P_{\min }} = 5M{I^2} + 2I{A^2} + 3I{B^2} = 5.3 + 2.27 + 3.12 = 105
Câu 42:
Cho hình chóp S.ABCD có chiều cao bằng 9 và đáy là hình bình hành có diện tích bằng 27. Gọi M,N,P,Q lần lượt là các trọng tâm của các mặt bên SAB, SBC, SCD, SDA. Tính thể tích khối đa diện lồi có các đỉnh A,B,C,D,M,N,P,Q.
 Xem đáp án
Xem đáp án
Đáp án B
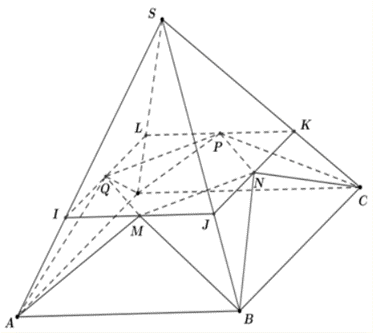
Thể tích khối chóp {V_{S.ABCD}} = \frac{1}{3}.9.27 = 81.
Gọi I, J, K, L lần lượt là giao điểm của mặt phẳng \left( {MNPQ} \right) và SA, SB, SC, SD.
Vì IJKL đồng dạng với ABCD theo tỉ số \frac{2}{3} nên {S_{IJKL}} = \frac{4}{9}{S_{ABCD}}.
Thể tích các khối chóp AIMQ, BJMN, CKNP, DLPQ bằng nhau và bằng
{V_2} = \frac{1}{3}.{S_{IMQ}}.d\left( {A,\left( {IMQ} \right)} \right) = \frac{1}{3}.\frac{1}{8}.{S_{MBPQ}}.\frac{1}{3}.d\left( {S,\left( {ABCD} \right)} \right)
= \frac{1}{3}.\frac{1}{8}.\frac{4}{9}.{S_{ABCD}}.\frac{1}{3}.d\left( {S,\left( {ABCD} \right)} \right) = \frac{1}{{54}}.81 = \frac{3}{2}.
Thể tích {V_1} = {V_{IJKL.ABCD}} = {V_{S.ABCD}} - {V_{S.IJKL}} = {V_{S.ABCD}} - \frac{1}{3}.{S_{IJKL}}.d\left( {S,\left( {IJKL} \right)} \right)
= {V_{S.ABCD}} - \frac{1}{3}.\frac{4}{9}.{S_{ABCD}}.\frac{2}{3}.d\left( {S,\left( {ABCD} \right)} \right) = \frac{{19}}{{27}}{V_{S.ABCD}} = 57.
Vậy thể tích cần tính bằng V = {V_1} - 4{V_2} = 57 - 4.\frac{3}{2} = 51.
Câu 43:
Xét các số phức z thỏa mãn z không phải là số thực và w = \frac{z}{{4 + z + {z^2}}} là số thực. Tìm giá trị lớn nhất {P_{\max }} của biểu thức P = \left| {z + 3 - 4i} \right|
 Xem đáp án
Xem đáp án
Đáp án B
Do w = \frac{z}{{4 + z + {z^2}}} là số thực nên \frac{{4 + z + {z^2}}}{z} = \frac{4}{z} + 1 + z là một số thực
Đặt z = a + bi\left( {a,b \in \mathbb{R},b \ne 0} \right) ta có: \frac{4}{{a + bi}} + a + bi = \frac{{4\left( {a - bi} \right)}}{{{a^2} + {b^2}}} + a + bi là số thực
Suy ra phần ảo
Do đó tập hợp điểm M biểu diễn số phức z là đường tròn tâm O\left( {0;0} \right) bán kính R = 2.
Vậy {P_{\max }} = R + OE với E\left( { - 3;4} \right) \Rightarrow {P_{\max }} = 2 + 5 = 7.
Câu 44:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn \left[ { - 10;10} \right] để bất phương trình {\log _3}\frac{{2{x^2} + x + m + 1}}{{{x^2} + x + 1}} \ge 2{x^2} + 4x + 5 - 2m có nghiệm. Số phần tử của tập hợp S bằng
 Xem đáp án
Xem đáp án
Đáp án B
Để ý vế trái có 2m nên bất phương trình tương đương
{\log _3}\left( {2{x^2} + x + m + 1} \right) + 2\left( {2{x^2} + x + m + 1} \right) \ge {\log _3}\left( {{x^2} + x + 1} \right) + 6\left( {{x^2} + x + 1} \right) + 1
\Leftrightarrow {\log _3}\left( {2{x^2} + x + n + 1} \right) + 2\left( {2{x^2} + x + m + 1} \right) \ge {\log _3}\left( {3{x^2} + 3x + 3} \right) + 6\left( {{x^2} + x + 1} \right)
Sử dụng hàm số tương đồng
f\left( t \right) = {\log _3}t + 2t \Rightarrow f\left( t \right) \uparrow \Rightarrow f\left( {2{x^2} + x + m + 1} \right) \ge f\left( {3{x^2} + 3x + 3} \right)
\Leftrightarrow 2{x^2} + x + m + 1 \ge 3{x^2} + 3x + 3 \Leftrightarrow m \ge {x^2} + 2x + 2 \Leftrightarrow m \ge {\left( {x + 1} \right)^2} + 1
Bất phương trình có nghiệm khi m \ge \min \left[ {{{\left( {x + 1} \right)}^2} + 1} \right] = 1, suy ra 10 giá trị nguyên m.
Câu 45:
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đồ thị y = f'\left( x \right) như hình vẽ. Đặt g\left( x \right) = 2f\left( x \right) - {\left( {x - 1} \right)^2}. Khi đó giá trị nhỏ nhất của hàm số y = g\left( x \right) trên đoạn \left[ { - 3;3} \right] bằng
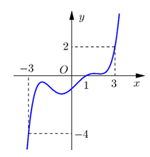
 Xem đáp án
Xem đáp án
Đáp án C
Ta có g'\left( x \right) = 2\left[ {f'\left( x \right) - \left( {x - 1} \right)} \right]
g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x - 1 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = 3\end{array} \right.
Ta có bảng biến thiên của hàm số y = g\left( x \right)
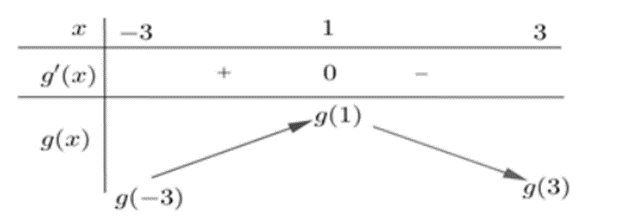
Từ bảng biến thiên \Rightarrow \mathop {\min }\limits_{\left[ { - 3;3} \right]} g\left( x \right) \in \left\{ {g\left( 3 \right);g\left( { - 3} \right)} \right\}
Ta có \int\limits_{ - 3}^1 {g'\left( x \right)} dx > \int\limits_1^3 { - g'\left( x \right)dx} \Leftrightarrow g\left( 1 \right) - g\left( { - 3} \right) > g\left( 1 \right) - g\left( 3 \right) \Leftrightarrow g\left( { - 3} \right) < g\left( 3 \right)
Vậy giá trị nhỏ nhất của hàm số g\left( x \right) trên đoạn \left[ { - 3;3} \right] bằng g\left( { - 3} \right).
Câu 46:
Số các giá trị nguyên của m để hàm số f\left( x \right) = \frac{1}{3}{x^3} - \left( {m + 50} \right){x^2} + \left( {{m^2} + 100m} \right)x + 2020m nghịch biến trên \left( {7;13} \right) là
 Xem đáp án
Xem đáp án
Đáp án A
Tập xác định: D = \mathbb{R}.
Ta có, f'\left( x \right) = {x^2} - 2\left( {m + 50} \right)x + {m^2} + 100m
Để hàm số nghịch biến trên \left( {7;13} \right) thì phương trình f'\left( x \right) = 0 phải có hai nghiệm {x_1},{x_2} thỏa mãn \left\{ \begin{array}{l}{x_1} \le 7\\{x_2} \ge 13\end{array} \right..
Từ đó, ta có hệ phương trình: \left\{ \begin{array}{l}\Delta ' = {\left[ { - \left( {m + 50} \right)} \right]^2} - \left( {{m^2} + 100m} \right) = 2500 > 0,\forall m\\{x_1} = m \le 7\\{x_2} = m + 100 \ge 13\end{array} \right.
\Leftrightarrow \left\{ \begin{array}{l}m \le 7\\m \ge - 87\end{array} \right. \Leftrightarrow - 87 \le m \le 7
Do m nguyên, cho nên tập hợp các giá trị của m là: S = \left\{ { - 87; - 86;...;6;7} \right\}
Có 95 giá trị nguyên của m thỏa mãn.
Câu 47:
Cho phương trình {\log _3}^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0. Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc \left[ {1;81} \right] là
 Xem đáp án
Xem đáp án
Đáp án C
+) Ta có \log _3^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0. Đặt t = {\log _3}x. Vì x \in \left[ {1;81} \right] nên t \in \left[ {0;4} \right].
Khi đó phương trình đã cho trở thành: {t^2} - \left( {m + 1} \right)t + 3m - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = m - 2\end{array} \right.
+) Ycbt \Leftrightarrow \left\{ \begin{array}{l}0 \le m - 2 \le 4\\m - 2 \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 \le m \le 6\\m \ne 5\end{array} \right.. Vậy có 4 số nguyên m thỏa ycbt.
Câu 48:
Trong không gian tọa độ Oxyz, cho ba mặt phẳng (\left( {{P_1}} \right):\;2x + y + 2z - 5 = 0,\;\left( {{P_2}} \right):\;2x + y + 2z + 13 = 0, \left( Q \right):\;2x - 2y - z - 5 = 0, và điểm A\left( { - 2;0;0} \right) nằm giữa hai mặt phẳng \left( {{P_1}} \right),\;\left( {{P_2}} \right). Mặt cầu (S) có tâm I\left( {a;b;c} \right) luôn đi qua A và tiếp xúc với hai mặt phẳng \left( {{P_1}} \right),\;\left( {{P_2}} \right). Khi khối cầu \left( S \right) cắt mặt phẳng (Q) theo thiết diện là hình tròn có diện tích lớn nhất thì a + b - 2c bằng
 Xem đáp án
Xem đáp án
Đáp án B
Mặt phẳng cách đều hai mặt phẳng \left( {{P_1}} \right),\left( {{P_2}} \right) có phương trình dạng \left( P \right):2x + y + 2z + D = 0
Lại có d\left( {{P_1};P} \right) = d\left( {{P_2};P} \right) \Leftrightarrow \frac{{\left| {D + 5} \right|}}{{\sqrt {4 + 1 + 4} }} = \frac{{\left| {D - 13} \right|}}{{\sqrt {4 + 1 + 4} }} \Leftrightarrow \left| {P + 5} \right| = \left| {P - 13} \right| \Leftrightarrow \left[ \begin{array}{l}{\rm{D}} + 5 = D - 13\\D + 5 = 13 - D\end{array} \right. \Leftrightarrow D = 4
Vậy \left( P \right):2x + y + 2z + 4 = 0. Tâm I \in \left( P \right) và điểm A \in \left( P \right)
Điểm I nằm trên giao tuyến của mặt cầu \left( {A;R} \right) với R = d\left( {{P_1};\left( P \right)} \right) = 3 và mặt phẳng \left( P \right)
Mặt phẳng \left( P \right) \bot \left( Q \right), để \left( S \right) cắt mặt phẳng \left( Q \right) theo thiết diện là hình tròn có diện tích lớn nhất thì d{\left( {I;\left( Q \right)} \right)_{\min }}
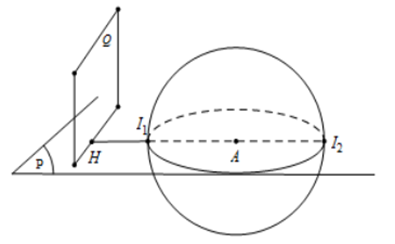
Để d{\left( {I;\left( Q \right)} \right)_{\min }} thì I = AH \cap \left( {A;R} \right), phương trình \(AH:\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 2t\\z = - t\end{array} \right.\)
Gọi I\left( { - 2 + 2t; - 2t; - t} \right) \Rightarrow I{A^2} = 9{t^2} = 9 \Leftrightarrow t = \pm 1 \Rightarrow \left[ \begin{array}{l}I\left( {0; - 2; - 1} \right)\\I\left( { - 4;2;1} \right)\end{array} \right.
Kiểm tra khoảng cách từ I đến \left( Q \right) suy ra I\left( {0; - 2; - 1} \right) là điểm cần tìm.
Câu 49:
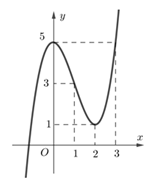
Cho hàm số y = f\left( x \right) liên tục có đạo hàm trên \mathbb{R}, và có đồ thị như hình vẽ. Kí hiệu g\left( x \right) = f\left( {2\sqrt {2x} + \sqrt {1 - x} } \right) + m. Tìm điều kiện của tham số m để \mathop {Max}\limits_{\left[ {0;1} \right]} g\left( x \right) > 2\mathop {Min}\limits_{\left[ {0;1} \right]} g\left( x \right).
 Xem đáp án
Xem đáp án
Đáp án A
Đặt t = 2\sqrt {2x} + \sqrt {1 - x} với x \in \left[ {0;1} \right] ta có t' = 2\sqrt 2 .\frac{1}{{2\sqrt x }} - \frac{1}{{2\sqrt {1 - x} }} = 0 \Leftrightarrow 2\sqrt 2 \sqrt {1 - x} = \sqrt x
\Leftrightarrow 8\left( {1 - x} \right) = x \Leftrightarrow x = \frac{8}{9}
Mặt khác t\left( 0 \right) = 1,t\left( {\frac{8}{9}} \right) = 3,t\left( 1 \right) = 2\sqrt 2 suy ra t \in \left[ {1;3} \right]
Với t \in \left[ {1;3} \right] thì g\left( x \right) = f\left( t \right) \in \left[ {1;5} \right] do đó \mathop {Max}\limits_{\left[ {0;1} \right]} g\left( x \right) = 5 + m,\mathop {Min}\limits_{\left[ {0;1} \right]} g\left( x \right) = 1 + m
Giả thiết \Leftrightarrow 5 + m > 2\left( {m + 1} \right) \Leftrightarrow m < 3.
Câu 50:
Có bao nhiêu giá trị nguyên dương của tham số m để tồn tại các số thực x,y thỏa mãn đồng thời {e^{3x + 5y - 10}} - {e^{x + 3y - 9}} = 1 - 2x - 2y và \log _5^2(3x + 2y + 4) - (m + 6){\log _5}(x + 5) + {m^2} + 9 = 0?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có {e^{3x + 5y - 10}} - {e^{x + 3y - 9}} = 1 - 2x - 2y \Leftrightarrow {e^{3x + 5y - 10}} - {e^{x + 3y - 9}} = \left( {x + 3y - 9} \right) - \left( {3x + 5y - 10} \right)
\Leftrightarrow {e^{3x + 5y - 10}} + \left( {3x + 5y - 10} \right) = {e^{x + 3y - 9}} + \left( {x + 3y - 9} \right)
\Leftrightarrow f\left( {3x + 5y - 10} \right) = f\left( {x + 3y - 9} \right) (1)
Với f\left( t \right) = {e^t} + t. Vì f'\left( t \right) = {e^t} + 1 > 0\,\,\forall t \in \mathbb{R} nên f\left( t \right) là hàm số đồng biến trên R.
Do đó \left( 1 \right) \Leftrightarrow 3x + 5y - 10 = x + 3y - 9 \Leftrightarrow 2y = 1 - 2x.
Thay vào điều kiện còn lại trong đề bài ta được phương trình
\log _5^2\left( {x + 5} \right) - \left( {m + 6} \right){\log _5}\left( {x + 5} \right) + {m^2} + 9 = 0 (2)
Bài toán được thỏa mãn khi và chỉ khi phương trình (2) có nghiệm x, điều này xảy ra khi
\Delta = 3{m^2} + 12m \ge 0 \Leftrightarrow 0 \le m \le 4 \Rightarrow m = 1,m = 2,m = 3,m = 4 (vì m là số nguyên dương).
