Biết \[\int\limits_1^e {\frac{{\ln x}}{{x\left( {\ln x + 2} \right)}}{\rm{d}}x = a\ln 3 + b\ln 2 + c,{\mkern 1mu} {\mkern 1mu} (a,b,c \in Q).} \] Tính giá trị của \[S = {a^2} + {b^2} + {c^2}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Đặt \(t = \ln x \Rightarrow dt = \frac{{dx}}{x}\). Đổi cận \(\left[ \begin{array}{l}x = 1 \Rightarrow t = 0\\x = e \Rightarrow t = 1\end{array} \right.\).
Khi đó \(\int\limits_1^e {\frac{{\ln x}}{{x\left( {\ln x + 2} \right)}}dx} = \int\limits_0^1 {\frac{t}{{t + 2}}dt} = \left. {\left( {t - 2\ln \left| {t + 2} \right|} \right)} \right|_0^1 = - 2\ln 3 + 2\ln 2 + 1\)
Suy ra \(a = - 2,{\rm{ }}b = 2,{\rm{ }}c = 1 \Rightarrow S = {a^2} + {b^2} + {c^2} = 9\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):2x + 2y - z + 9 = 0\] và điểm \[A\left( {1;2; - 3} \right).\] Đường thẳng d đi qua A và có vectơ chỉ phương \[\vec u = \left( {3;4; - 4} \right)\] cắt (P) tại B. Điểm M thay đổi trên (P) sao cho M luôn nhìn đoạn AB dưới một góc \[{90^0}\]. Độ dài đoạn MB lớn nhất bằng
Cho hàm số \[y = f\left( x \right)\] là hàm số bậc ba có bảng biến thiên như hình vẽ
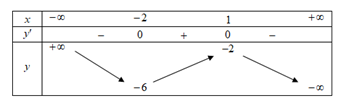
Số đường tiệm cận đứng và ngang của đồ thị hàm số \[y = \frac{{2x + 7 - 3\sqrt {4x + 5} }}{{\left| {f\left( x \right)} \right| - 2}}\] là
Một chất điểm đang chuyển động với vận tốc \[{v_0} = 15{\mkern 1mu} m/s\] thì tăng tốc với gia tốc \[a\left( t \right) = {t^2} + 4t{\mkern 1mu} \left( {m/{s^2}} \right).\] Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc.
Cho hàm số \[y = f\left( x \right)\] có bảng xét dấu của đạo hàm như sau.
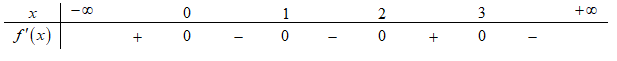
Hàm số \[y = f\left( {x - 1} \right) + {x^3} - 12x + 2019\] nghịch biến trên khoảng nào dưới đây?
Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC, với \[A\left( {1;2;1} \right),B\left( { - 3;0;3} \right),C\left( {2;4; - 1} \right).\] Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
Trong không gian Oxyz, cho mặt cầu \[(S):{(x + 2)^2} + {(y - 1)^2} + {(z + \sqrt 2 )^2} = 9\] và hai điểm \[A( - 2;0; - 2\sqrt 2 ),B( - 4; - 4;0)\]. Biết rằng tập hợp các điểm M thuộc \[(S)\] sao cho \[M{A^2} + \overrightarrow {MO} .\overrightarrow {MB} = 16\] là một đường tròn. Bán kính của đường tròn đó bằng
Cho tích phân \[I = \int\limits_0^4 {f\left( x \right)dx} = 32.\] Tính tích phân \[J = \int\limits_0^2 {f\left( {2x} \right)dx} \].
Cho số phức z thỏa mãn \[(2 + 3i)z + 4 - 3i = 13 + 4i\]. Môđun của z bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật \[AB = a\], \[AD = 2a\], cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng \[\frac{{2{a^3}}}{3}\] . Tính góc tạo bởi đường thẳng SB với mặt phẳng \[\left( {ABCD} \right)\].
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh a. Gọi M, N lần lượt là trung điểm của cạnh \[A'B'\] và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnhA và \[(H')\] là khối đa diện còn lại. Tính tỉ số \[\frac{{{V_{(H)}}}}{{{V_{(H')}}}}.\]
Trong không gian Oxyz, cho \[A\left( {1;3;5} \right)\], \[B\left( { - 5; - 3; - 1} \right)\]. Phương trình mặt cầu đường kính AB là:
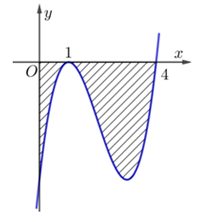
Diện tích hình phẳng giới hạn bởi đồ thị hàm số bậc ba \[y = f\left( x \right)\] và các trục tọa độ là \[S = 32\] (hình vẽ bên). Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng trên quanh trục \[Ox.\]
Tìm họ nguyên hàm của hàm số \[y = {x^2} - {3^x} + \frac{1}{x}.\]
Gọi \[M,m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} + x + 3}}{{x - 2}}\] trên \[\left[ { - 2;1} \right].\] Tính \[T = M + 2m.\]