Cho \[a,{\rm{ }}b\] là các số thực dương thỏa mãn \[b > 1\] và \[\sqrt a \le b < a.\] Giá trị nhỏ nhất của biểu thức \[P = {\log _{\frac{a}{b}}}a + 2{\log _{\sqrt b }}\left( {\frac{a}{b}} \right)\] bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Ta có \(P = \frac{1}{{{{\log }_a}\frac{a}{b}}} + 4{\log _b}\frac{a}{b} = \frac{1}{{1 - {{\log }_a}b}} + 4\left( {{{\log }_b}a - 1} \right) = \frac{1}{{1 - {{\log }_a}b}} + \frac{4}{{{{\log }_a}b}} - 4.\)
Đặt \(t = {\log _a}b \Rightarrow P = \frac{1}{{1 - t}} + \frac{4}{t} - 4.\)
Từ \(a > \sqrt a \Rightarrow a > 1 \Rightarrow t = {\log _a}b < {\log _a}a \Rightarrow t < 1.\)
Từ \(b \ge \sqrt a \Rightarrow t = {\log _a}b \ge {\log _a}\sqrt a = \frac{1}{2} \Rightarrow \frac{1}{2} \le t < 1.\)
Xét hàm số \(f\left( t \right) = \frac{1}{{1 - t}} + \frac{4}{t} - 4\), với \(t \in \left[ {\frac{1}{2};1} \right)\) có \(\left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{f'\left( t \right) = \frac{1}{{{{\left( {1 - t} \right)}^2}}} - \frac{4}{{{t^2}}} = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t \in \left( {\frac{1}{2};1} \right)}\\{t = 2\left( {1 - t} \right)}\end{array}} \right. \Leftrightarrow t = \frac{2}{3}.\)
Xét bảng sau:
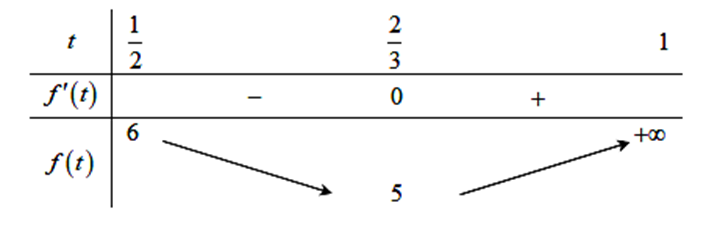
Từ đó \(\mathop {\min }\limits_{\left[ {\frac{1}{2};1} \right)} f\left( t \right) = 5\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \[y = \frac{{mx + 7m - 8}}{{x - m}}\], với m là tham số thực. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định?
Biết rằng \[\int\limits_2^4 {\frac{{{x^3} + 2}}{{{x^2} + x}}dx} = a + b\ln 2 + c\ln 3 + d\ln 5,\] với \[a,{\rm{ }}b,{\rm{ }}c,{\rm{ }}d \in \mathbb{Z}.\] Tính giá trị của biểu thức \[S = a + b + c + d.\]
Tìm giá trị nhỏ nhất \[{y_{\min }}\] của hàm số \[y = {x^4} - 4{x^3} + 8x.\]
Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.
Có bao nhiêu số phức \[z\] thỏa mãn \[\left( {1 + i} \right)z + \bar z\] là số thuần ảo và \[\left| {z - 2i} \right| = 1\]?
Họ tất cả các nguyên hàm của hàm số \[f\left( x \right) = {e^{4x + 3}}\] là
Trong không gian Oxyz, cho đường thẳng \[d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1\\z = 3 + 2t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right).\] Đường thẳng d đi qua điểm có tọa độ nào dưới đây?
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Khoảng cách từ điểm A đến mặt phẳng \[\left( {SBC} \right)\] bằng
Cho \[\int\limits_0^1 {f\left( x \right)dx} = 2\] và \[\int\limits_1^2 {f\left( x \right)dx} = - 3.\] Tích phân \[\int\limits_0^2 {f\left( x \right)dx} \] bằng
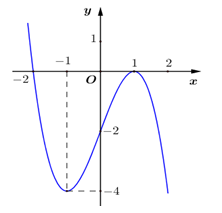
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Tìm tập xác định D của hàm số \[y = {\left( {{x^2} - 6x + 8} \right)^{\frac{1}{{2020}}}}.\]
Cho ba số phức \[{z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\] thỏa mãn \[\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\]; \[\left| {{z_1} - {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\] và \[z_1^2 = {z_2}{z_3}.\] Tính giá trị của \[\left| {{z_2} - {z_3}} \right| - \left| {{z_3} - {z_1}} \right|\].
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \[d:\left\{ \begin{array}{l}x = 3 + 3t\\y = 4 + 2t\\z = 2 + t\end{array} \right.{\rm{ }}\left( {t \in \mathbb{R}} \right).\] Xét đường thẳng \[\Delta :\frac{{x - 2}}{6} = \frac{{y - 1}}{4} = \frac{{z + 3}}{m},\] với m là tham số thực khác 0. Tìm tất cả các giá trị thực của m để đường thẳng \[\Delta \] song song với đường thẳng \[d.\]
Trong không gian, cho hình thang cân ABCD có đáy nhỏ \[AB = 1\], đáy lớn \[CD = 3\] và cạnh bên \[AD = \sqrt 2 .\] Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD xung quanh trục \[AB.\]
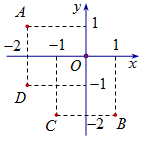
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \[z = - 1 - 2i\]?