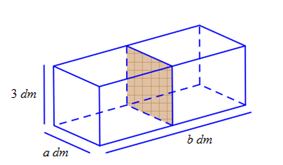
Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích $72d{m^3}$ và chiều cao là $3dm.$ Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bề dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.

Cho $a,{\rm{ }}b$ là các số thực dương thỏa mãn ${a^2} + {b^2} = 8ab.$ Mệnh đề nào dưới đây là đúng?

Biết rằng $\int\limits_2^3 {\frac{{x + 1}}{{x\left( {x - 2} \right) + 1}}dx} = a + b\ln 2,$ với $a,{\rm{ }}b \in \mathbb{Z}.$ Tính $S = a + 2b.$

Tính thể tích của khối lập phương $ABCD.A'B'C'D'$, biết $AC' = 2a\sqrt 3 .$

Cho hàm số $y = {x^3} - 3m{x^2} + 3\left( {2{m^2} - 10m + 9} \right)x$. Có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, $AC = \frac{{a\sqrt 2 }}{2}.$ Cạnh bên SA vuông góc với mặt phẳng đáy và đường thẳng SB tạo với mặt phẳng $\left( {ABCD} \right)$ một góc $60^\circ .$ Khoảng cách giữa hai đường thẳng $AD$ và $SC$ bằng

Tính môđun của số phức z thỏa mãn $z\left( {1 - i} \right) + 2i = 1.$

Tìm số tiệm cận đứng của đồ thị hàm số $y = \frac{{\sqrt {x + 1} + \sqrt {x + 4} - 3}}{{{x^3} - x}}.$

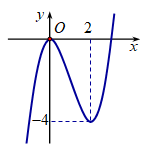
Cho hàm số f(x) có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số $y = f\left[ {f\left( x \right)} \right]$.

Trong không gian Oxyz, cho hai đường thẳng ${d_1}:\frac{{x - 1}}{1} = \frac{y}{1} = \frac{{z - 1}}{{ - 1}}$ và ${d_2}:\frac{{x + 4}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z + 3}}{1}.$ Mặt phẳng $\left( Q \right):ax + by + cz - 4 = 0$ chứa đường thẳng ${d_1}$ và song song với đường thẳng ${d_2}.$ Tính $a + b + c.$

Trong không gian Oxyz, cho mặt phẳng $\left( P \right):x + 2y - 3z + 3 = 0.$ Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?

Cho hàm số f(x) có bảng biến thiên như sau:

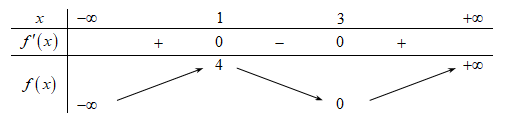
Phương trình $3f\left( x \right) - 2 = 0$ có số nghiệm thực là

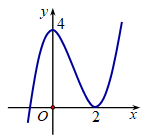
Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và đồ thị hàm số $y = f'\left( x \right)$ như hình vẽ. Bất phương trình $f\left( x \right) > {x^3} + 4x + m$ nghiệm đúng với mọi $x \in \left( {0;2} \right)$ khi và chỉ khi

Tập nghiệm của phương trình $\frac{1}{2}{\log _3}{\left( {x + 2} \right)^2} + \frac{1}{3}{\log _3}{\left( {4x - 1} \right)^3} = 2$ là

Cho hàm số $y = f\left( x \right)$ có đạo hàm tại $x = 1$ và $f'\left( 1 \right) \ne 0.$ Gọi ${d_1}$, ${d_2}$ lần lượt là hai tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right) = x.f\left( {2x - 1} \right)$ tại điểm có hoành độ $x = 1.$ Biết rằng hai đường thẳng ${d_1}$, ${d_2}$ vuông góc với nhau. Khẳng định nào sau đây đúng?

Cho hai số phức z, w thỏa mãn $\left| {z + 2w} \right| = 3$, $\left| {2z + 3w} \right| = 6$ và $\left| {z + 4w} \right| = 7$. Tính giá trị của biểu thức $P = z.\bar w + \bar z.w$.