Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình tròn là 20 mét và 15 mét. Khoảng cách giữa hai tâm của hai hình tròn là 30 mét. Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 ngàn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 ngàn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào trong các số dưới đây?
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Gọi O, I lần lượt là tâm của các đường tròn bán kính bằng 20 mét và bán kính bằng 15 mét.
Gắn hệ trục Oxy, vì OI=30 mét nên I(0;30).
Phương trình hai đường tròn lần lượt là và .
Gọi A, B là các giao điểm của hai đường tròn đó.
Tọa độ A, B là nghiệm của hệ .
Tổng diện tích hai đường tròn là .
Phần giao của hai hình tròn chính là phần hình phẳng giới hạn bởi hai đồ thị và .
Do đó diện tích phần giao giữa hai hình tròn là .
Số tiền để làm phần giao giữa hai hình tròn là: (đồng).
Số tiền để làm phần còn lại là: (đồng).
Vậy tổng số tiền làm sân khấu là: (đồng).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bất phương trình nghiệm đúng với mọi khi và chỉ khi
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a. Cạnh bên SA vuông góc với đáy, góc giữa SD với đáy bằng . Tính khoảng cách d từ điểm C đến mặt phẳng (SBD) theo a.
Cho khối nón có độ dài đường sinh bằng đường kính đáy bằng a. Thể tích của khối nón là
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;3), B(-1;0;1). Trọng tâm G của tam giác OAB có tọa độ là
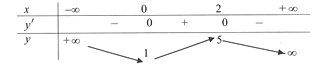
Giá trị cực đại của hàm số đã cho bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh , . Hai mặt bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính theo a thể tích V của khối chóp S.ABCD.
Trong không gian hệ tọa độ Oxyz, cho mặt phẳng và mặt phẳng(P) không qua O, song song mặt phẳng (Q) và . Phương trình mặt phẳng (P) là
Cho mặt cầu có diện tích đường tròn lớn là 2π. Khi đó, mặt cầu có bán kính là:
Tích tất cả các số thực m để hàm số có giá trị nhỏ nhất trên đoạn [0;3] bằng 18 là
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a và cạnh bên bằng . Lấy M, N lần lượt trên cạnh AB', A'C sao cho . Tính thể tích V của khối BMNC'C.