Trong không gian Oxyz, cho bốn đường thẳng: d1:x−31=y+1−2=z+11 , d2:x1=y−2=z−11 , d3:x−12=y+11=z−11 , d4:x1=y−1−1=z−11 . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là
D. Vô số.
Giải bởi Vietjack
Đáp án B
Đường thẳng d1 đi qua điểm M1=(3;−1;−1) và có một véctơ chỉ phương là →u1=(1;−2;1) .
Đường thẳng d2 đi qua điểm M2=(0;0;1) và có một véctơ chỉ phương là →u2=(1;−2;1) .
Do →u1=→u2 và M1∉d1 nên hai đường thẳng d1 và d2 song song với nhau.
Ta có →M1M2=(−3;1;2), [→u1,→M1M2]=(−5;−5;−5)=5(1;1;1) .
Gọi (α) là mặt phẳng chứa d1 và d2 khi đó (α) có một véctơ pháp tuyến là →n=(1;1;1) .
Phương trình mặt phẳng (α) là x+y+z−1=0 .
Gọi A=d3∩(α) thì A(1;−1;1) .
Gọi B=d4∩(α) thì B(−1;2;0) .
Do →AB=(−2;3;−1) không cùng phương với →u1=(1;−2;1) nên đường thẳng AB cắt hai đường thẳng d1 và d2 .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Có bao nhiêu số nguyên M thuộc khoảng (−10;10) để hàm số y=|2x2−2mx+3| đồng biến trên (1;+∞) ?
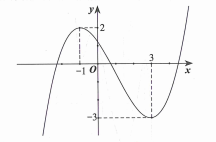
Cho hàm số f(x) có đạo hàm, liên tục trên đoạn [0;1] và thỏa mãn các điều kiệnf(1)=0 và 1∫0[f' . Tính tích phân bằng
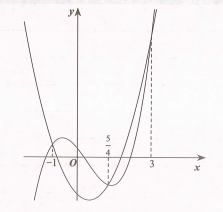
Biết rằng là một nguyên hàm của hàm số trên khoảng . Gọi là một nguyên hàm của thỏa mãn , giá trị của bằng
![Cho hàm số f(x) liên tục trên đoạn [-1;4] và có đồ thị trên đoạn [-1;4] như hình vẽ bên. Tích phân từ -1 đến 4 của f(x)dx bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/333-1653482408.png)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng và . Tìm m để và song song với nhau.
