Cho hình chóp S.ABCD có SA vuông góc với đáy; . Đáy ABCD là hình thang vuông tại A và B, . Gọi E là trung điểm AD. Tính bán
kính mặt cầu ngoại tiếp hình chóp S.ECD.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
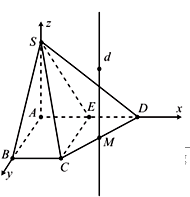
Vì E là trung điểm AD và nên mà tứ giác ABCE là hình vuông suy ra hay tam giác ECD vuông tại E nên M là tâm đường tròn ngoại tiếp .
Gắn với hệ trục tọa độ với .
Coi đơn vị độ dài là a=1
Suy ra và là trung điểm của CD.
Vì vuông tại E nên tâm mặt cầu ngoại tiếp hình chóp S.ECD thuộc đường thẳng qua M và song song với SA.
Phương trình đường thẳng d qua M và song song với SA có 1 véctơ pháp tuyến thì có dạng:
Suy ra là tâm mặt cầu ngoại tiếp chóp S.ECD thì:
Bán kính mặt cầu là hay .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian Oxyz, cho . Phương trình mặt phẳng (P) sao cho nằm về hai phía (P) và (P) cách đều .
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình có đúng 6 nghiệm phân biệt thuộc đoạn là
![Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình f^2(cosx)+(m-2018)f(cosx)+m-2019=0 có đúng 6 nghiệm phân biệt thuộc đoạn [0; 2 pi] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/x-1655339013.png)
Mặt phẳng nào dưới đây cắt mặt cầu theo thiết diện là một đường tròn?
Gọi S là tập các giá trị của tham số m để đường thẳng cắt đồ thị hàm số tại đúng một điểm. Tích phân các phần tử của S bằng.
Cho hàm số (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số . Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng là
Biết rằng đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt A và B, biết điểm B có hoành độ âm. Hoành độ của điểm B bằng
Với giá trị thực nào của tham số m thì đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt M, N sao cho MN ngắn nhất?
Một thùng rượu có bán kính đáy là thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40 cm, chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (đơn vị lít) là bao nhiêu?
