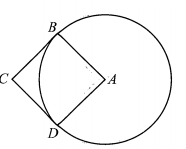
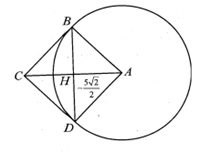
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Khối tròn xoay được tạo thành khi quay mô hình quanh trục AC bao gồm:
- Khối cầu có bán kính .
- Khối nón có chiều cao và bán kính đường tròn đáy là
.
Trừ đi phần giao của khối cầu và khối nón chính là chỏm cầu có chiều cao
Vậy thể tích khối nón xoay cần tìm là
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn là
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm y=f'(x) như sau

Khẳng định nào sau đây đúng?
Một miếng tôn hình chữ nhật có kích thước là 4 ´ 6 được dùng để làm mặt trụ của một cái xô hình trụ, có hai phương án làm với chiều cao lần lượt là h=4 và h=6 làm được xô có thể tích tương đương là và . Bỏ qua độ dày mép dán, tỉ số là
Cho hàm số y=f(x) có bảng biến thiên như sau:
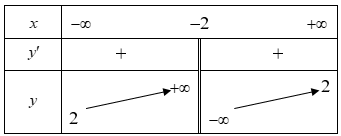
Đường tiệm cận đứng của đồ thị hàm số đã cho là
Điều kiện của tham số m để phương trình có nhiều hơn một nghiệm là
Cho hình lập phươngABCD.A'B'C'D' . Góc giữa hai mặt phẳng (A'B'CD) và (ABC'D') bằng
Tổng tất cả các nghiệm nguyên không âm của bất phương trình bằng
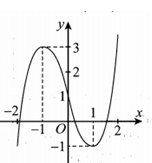
Cho hàm số bậc ba y=f(x) có đồ thị trong hình bên. Số nghiệm của phương trình f(x)=2 là
Trong không gian Oxyz, phương trình mặt cầu có tâm I(2;1;-5) và tiếp xúc với mặt phẳng là