Cho hình lăng trụ tứ giác đều . Biết và cạnh bên . Thể tích lăng trụ đó là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
- Sử dụng công thức giải nhanh: Hình vuông cạnh a có đường chéo bằng .
- Tính diện tích đáy, sau đó tính thể tích lăng trụ.
Giải chi tiết:
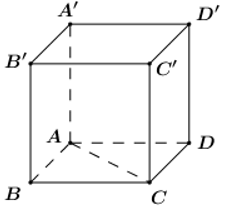
Vì là hình vuông có nên .
Vậy .
Đáp án A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một hộp đựng 40 tấm thẻ được đánh số thứ tự từ 1 đến 40. Rút ngẫu nhiên 10 tấm thẻ. Tính xác suất để lấy được 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn, trong đó có đúng một thẻ mang số chia hết cho 6.
Có hai bút chì màu, các bút chì khác nhau. Hộp thứ nhất có 5 bút chì màu đỏ và 7 bút chì màu xanh. Hộp thứ hai có 8 bút chì đỏ và 4 bút chì màu xanh. Chọn ngẫu nhiên mỗi hộp một cây bút chì. Xác suất để có 1 cây bút chì màu đỏ và 1 cây bút chì màu xanh là:
Cho hàm số có đạo hàm liên tục trên R và có đồ thị hàm số như hình vẽ bên dưới. Xét hàm số và các mệnh đề sau:
I. Hàm số có 3 điểm cực trị.
II. Hàm số đạt cực tiểu tại
III. Hàm số đạt cực đại tại
IV. Hàm số đồng biến trên khoảng
V. Hàm số nghịch biến trên khoảng
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Cho hàm số Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có giá trị nhỏ nhất không vượt quá 5?
Cho hình chóp có đáy là hình vuông cạnh 2a cạnh bên mặt bên là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng:
Trong bài thi thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua một sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? Biết dòng sông là thẳng, mục tiêu cách chiến sĩ 1km theo đường chim bay và chiến sĩ cách bờ bên kia 100m.
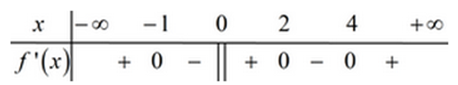
Có bao nhiêu số có ba chữ số đôi một khác nhau mà các chữ số đó thuộc tập hợp
Số các giá trị của tham số m để hàm số có giá trị lớn nhất trên bằng là: