Cho hình chóp có đáy là hình chữ nhật với . Cạnh bên SA vuông góc với đáy. Gọi M,N lần lượt là trung điểm của SB và SD. Tính khoảng cách d từ S đến mặt phẳng .
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
- Tính thể tích chóp , sử dụng tỉ lệ thể tích Simpson tính thể tích khối chóp .
- Sử dụng công thức
với p là nửa chu vi .
Giải chi tiết:
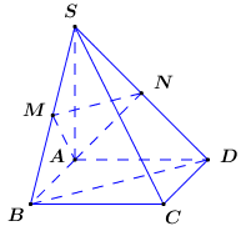
Áp dụng định lí Pytago trong các tam giác vuông ta có:
Khi đó ta có (đường trung tuyến trong tam giác vuông).
Ta có: MN là đường trung bình của nên .
Gọi p là nửa chu vi tam giác ta có: .
⇒ Diện tích tam giác là
Ta có: .
Mà .
Lại có , do đó .
Vậy
Đáp án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số có đồ thị là parabol như hình vẽ bên. Khẳng định nào sau đây là đúng?
Tính tổng các giá trị nguyên của tham số m trên để hàm số nghịch biến trên khoảng .
Cho các số thực thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tổng bằng:
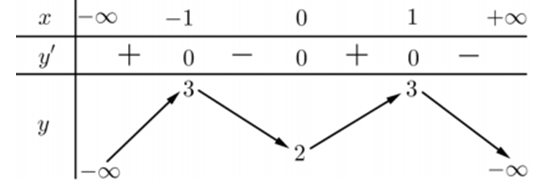
Trong bốn hàm số được liệt kẻ ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
Cho hàm số xác định, liên tục trên đoạn và có đồ thị là đường cong trong hình vẽ bên. Hàm số đạt cực đại tại điểm nào dưới đây?
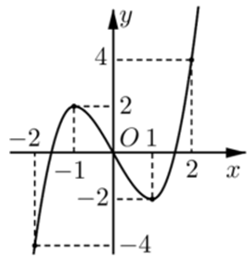
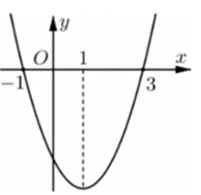
Cho hàm số có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng sau?
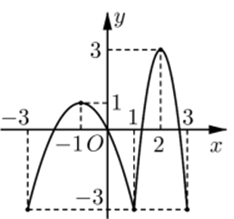
Hàm số với có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?