Cho hàm số \(f\left( x \right) = {x^3} + m{x^2} + nx - 1\) với \(m,n\) là các tham số thực thỏa mãn \(m + n >0\) và \(7 + 2\left( {2m + n} \right) < 0.\) Tìm số điểm cực trị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|.\)</>
A.9.
B.5.
C.11.
D. 2.
Giải bởi Vietjack
Giả thiết \(\left\{ \begin{array}{l}f\left( x \right) = {x^3} + m{x^2} + nx - 1\\m + n >0\\7 + 2\left( {2m + n} \right) < 0\end{array} \right.\)
Suy ra \(\left\{ \begin{array}{l}f\left( 0 \right) = - 2\\f\left( 1 \right) = m + n >0\\f\left( 2 \right) = 7 + 2\left( {2m + n} \right) < 0\\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}f\left( 0 \right).f\left( 1 \right) < 0\\f\left( 1 \right).f\left( 2 \right) < 0\\f\left( 2 \right) < 0\\\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \end{array} \right.\) (với lại \(f\left( x \right)\) liên tục trên \(\mathbb{R})\)
\( \Rightarrow f\left( x \right) = 0\) có 3 nghiệm lần lượt là \({x_1} \in \left( {0;1} \right),{x_2} \in \left( {1;2} \right),{x_3} \in \left( {2; + \infty } \right)\)
(do \(f\left( x \right)\) là đa thức bậc ba nên có tối đa 3 nghiệm.)
Như vậy đồ thị của hàm số \(y = f\left( x \right)\) có 2 điểm cực trị đều nằm bên phải trục tung.
Ta phác họa đồ thị \(y = f\left( x \right)\) như sau
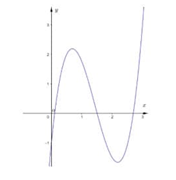
Từ đó suy ra đồ thị \(y = f\left( {\left| x \right|} \right)\) như hình bên dưới
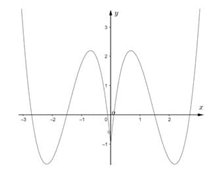
Cuối cùng, đồ thị của hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) như sau
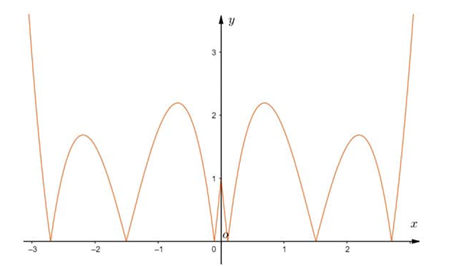
Kết luận, đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) có 11 điểm cực trị.
Đáp án C
Gói VIP thi online tại VietJack (chỉ 200k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = m{x^4} + \left( {m - 3} \right){x^2} + 3m - 5\) chỉ có cực tiểu mà không có cực đại.
Cho tứ diện \(ABCD\) có \(AB = 2a,AC = 3a,AD = 4a,\widehat {BAC} = \widehat {CAD} = \widehat {DAB} = {60^0}.\) Thể tích khối tứ diện \(ABCD\) bằng
Cho hàm số \(y = f\left( x \right).\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên.
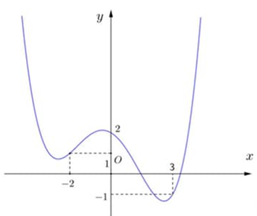
Hàm số \(g\left( x \right) = f\left( {x + 1} \right) + \frac{{{x^3}}}{3} - 3x\) nghịch biến trên khoảng nào dưới đây?
Tìm tất cả các giá trị của tham số \(m\) sao cho đồ thị hàm số \(y = \frac{{\sqrt {x - 1} + 2021}}{{\sqrt {{x^2} - 2mx + m + 2} }}\) có đúng ba đường tiệm cận.
Cho đường cong \(\left( C \right)\) có phương trình \(y = \frac{{x - 1}}{{x + 1}}.\) Gọi \(M\) là giao điểm của \(\left( C \right)\) với trục tung. Tiếp tuyến của \(\left( C \right)\) tại \(M\) có phương trình là
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên mỗi nửa khoảng \(\left( { - \infty ; - 2} \right]\) và \(\left[ {2; + \infty } \right)\) và có bảng biến thiên như dưới đây
![Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên mỗi nửa khoảng \(\left( { - \infty ; - 2} \right]\) và \(\left[ {2; + \infty } \right)\) và có bảng biến thiên như dưới đâyTìm tập (ảnh 1)](https://video.vietjack.com/upload2/images/1649527178/1649527356-image16.png)
Tìm tập hợp các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có hai nghiệm phân biệt.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Trên các đoạn \(SA,SB,SC,SD\) lấy lần lượt các điểm \(E,F,G,H\) thỏa mãn \(\frac{{SE}}{{SA}} = \frac{{SG}}{{SC}} = \frac{1}{3},\frac{{SF}}{{SB}} = \frac{{SH}}{{SD}} = \frac{2}{3}.\) Tỉ số thể tích khối \[EFGH\] với khối \(S.ABCD\) bằng:
Số giao điểm của hai đồ thị \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng số nghiệm phân biệt của phương trình nào sau đây?
Cho \(a\) là số thực dương và \(m,n\) là các số thực tùy ý. Trong các tính chất sau, tính chất nào đúng?
Với giá trị nào của \(m\) thì đồ thị hàm số \(y = \frac{{2{x^2} + 6mx + 4}}{{mx + 2}}\) đi qua điểm \(A\left( { - 1;4} \right)?\)
Giả sử các biểu thức chứa logarit đều có nghĩa. Mệnh đề nào sau đây đúng?
Xét khẳng định: “Với mọi số thực \(a\) và hai số hữu tỉ \(r,s\), ta có \({\left( {a'} \right)^2} = a{'^2}\)”. Với điều kiện nào trong các điều kiện sau thì khẳng định trên đúng.
Công thức tính thể tích khối chóp có diện tích đáy \(B\) và chiều cao \(h\) là
Tìm \(m\) để phương trình \({x^6} + 6{x^4} - {m^2}{x^3} + \left( {15 - 3{m^2}} \right){x^2} - 6mx + 10 = 0\) có đúng hai nghiệm phân biệt thuộc \[\left[ {\frac{1}{2};2} \right]?\]
