Cho hình chóp SABCD có đáy \(ABCD\) là hình thang vuông tại A và D. Cạnh bên SA vuông góc với mặt phẳng đáy,\(AB = 2a\), cạnh \(SC\) hợp với đáy một góc \({30^0}\).Tính thể tích khối chóp \(S.ABC\) theo a?
A.\[\frac{{{a^3}}}{3}\].
B.\[\frac{{{a^3}\sqrt 6 }}{6}\].
C.
D.\[\frac{{{a^3}\sqrt 6 }}{9}\].
 Giải bởi Vietjack
Giải bởi Vietjack
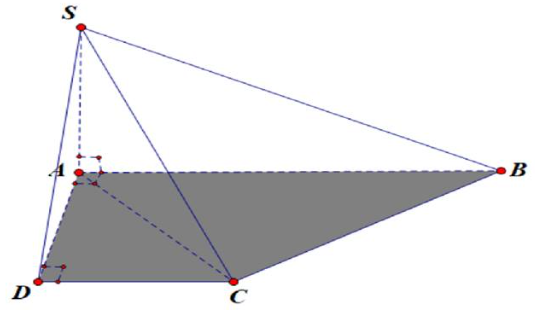
\(SA \bot \left( {ABCD} \right)\) nên \(\left( {\widehat {SC;\left( {ABCD} \right)}} \right) = \left( {\widehat {SC;AC}} \right) = \widehat {SCA}.\)
Tam giác \(ADC\) vuông tại \(D\) có \(AC = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 .\)
Tam giác \(SAC\) vuông tại \(A\) có \(SA = AC.\tan \left( {{{30}^0}} \right) = a\sqrt 2 .\frac{{\sqrt 3 }}{3} = \frac{{a\sqrt 6 }}{3}.\)
Diện tích tam giác \(ABC\) là \({S_{ABC}} = \frac{1}{2}AB.d\left( {C,AB} \right) = \frac{1}{2}AB.DA = \frac{1}{2}.2a.a = {a^2}\)
Thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}\frac{{a\sqrt 6 }}{3}.{a^2} = \frac{{{a^3}\sqrt 6 }}{9}.\)
Đáp án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình dưới:
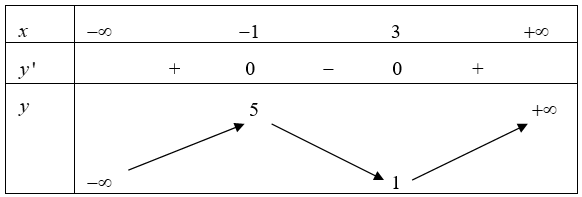
Số điểm cực trị của hàm số \(y = f\left( {{x^2} - 4{\rm{x}} + 1} \right)\)là:
Cho hàm số \(y = \frac{{2x + 2}}{{x - 1}}\). Trong các khẳng định sau, khẳng định nào là đúng:
Một vật chuyển động theo quy luật \(S = - {t^3} + 9{t^2} + t + 10\), với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(S\) (mét) là quảng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 12 giây, kể từ lúc bắt đầu chuyển động tại thời điểm \(t\) bằng bao nhiêu giây thì vật đạt vận tốc lớn nhất?
Cho hàm số \(y = a{x^4} + b{x^2} + c(a,b,c \in R)\)có đồ thị như hình vẽ bên.
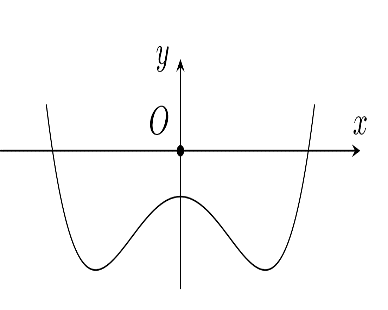
Số điểm cực trị của hàm số đã cho là?
Một khối lập phương có độ dài đường chéo bằng \(a\sqrt 6 \). Thể tích khối lập phương đó là:
Giá trị lớn nhất của hàm số \(f(x) = {x^4} - 4{x^2} + 5\)trên đoạn \([ - 2;3]\)bằng:
Cho hàm số \(y = f(x)\)có bảng xét dấu đạo hàm như sau

Mệnh đề nào dưới đây đúng?
Cho hàm số , với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên R?
Tìm tập xác định \[D\] của hàm số \(y = {\log _3}\left( {{x^2} - 4x + 3} \right)\).
Cho hàm số \(f\left( x \right) = \ln \frac{{2018x}}{{x + 1}}\). Tính tổng \(S = f'\left( 1 \right) + f'\left( 2 \right) + ... + f'\left( {2018} \right)\).
Cho khối chóp có diện tích đáy \(B = 6{a^2}\) và chiều cao \(h = 2a\). Thể tích khối chóp đã cho bằng:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
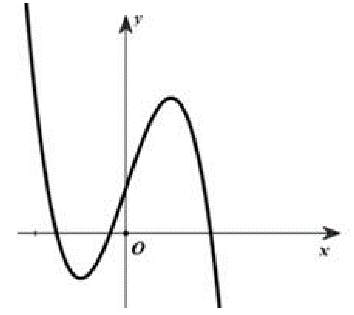
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \log \left( {{x^2} - 2mx + 4} \right)\) có tập xác định là \(\mathbb{R}\):