Tìm tất cả các giá trị thực của tham số \(m\) để đoạn \(\left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\) là tập hợp con của tập nghiệm bất phương trình \({\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 1} \right) < {\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 4\cos x + m} \right) + 1.\)</>
A.\(m \in \left( {\frac{7}{4};4} \right]\).
B.\(m \in \left[ {\frac{7}{4};4} \right)\).
C.\(m \in \left( {\frac{7}{4};4} \right)\).
D.\(m \in \left[ {\frac{7}{4};4} \right]\).
Giải bởi Vietjack
Để đoạn \(\left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\) là tập hợp con của tập nghiệm bất phương trình \({\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 1} \right) < {\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 4\cos x + m} \right) + 1\) thì:
\({\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 1} \right) < {\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 4\cos x + m} \right) + 1,\forall x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\)
\( \Leftrightarrow {\log _{\frac{1}{5}}}\left( {{{\cos }^2}x + 1} \right) < {\log _{\frac{1}{5}}}\left( {\frac{{{{\cos }^2}x + 4\cos x + m}}{5}} \right),\forall x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\cos ^2}x + 4\cos x + m >0\\5{\cos ^2}x + 5 >{\cos ^2}x + 4\cos x + m\end{array} \right.,\forall x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\)
\( \Leftrightarrow \left\{ \begin{array}{l}m >- {\cos ^2}x - 4\cos x\\m < 4{\cos ^2}x - 4\cos x + 5\end{array} \right.,\forall x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right]\)\(\left( 1 \right)\)
Đặt \(t = \cos x.\) Khi đó ta có (1) trở thành: \(\left\{ \begin{array}{l}m >- {t^2} - 4t\\m < 4{t^2} - 4t + 5\end{array} \right.,\forall t \in \left[ { - \frac{1}{2};1} \right].\)
+ Để \(m >- {t^2} - 4t,\forall t \in \left[ { - \frac{1}{2};1} \right] \Leftrightarrow m >\mathop {\max }\limits_{\left[ { - \frac{1}{2};1} \right]} \left( { - {t^2} - 4t} \right){\rm{ }}\left( 2 \right)\)
Xét hàm số \(f\left( { - \frac{1}{2}} \right) = \frac{7}{4};f\left( { - 1} \right) = - 5.\) Do đó \(\mathop {\max }\limits_{\left[ { - \frac{1}{2};1} \right]} f\left( t \right) = \frac{7}{4}.\) Nên \(\left( 2 \right) \Leftrightarrow m >\frac{7}{4}.\)
+ Để \(m < 4{t^2} - 4t + 5,\forall t \in \left[ { - \frac{1}{2};1} \right] \Leftrightarrow m < \mathop {\min }\limits_{\left[ { - \frac{1}{2};1} \right]} \left( {4{t^2} - 4t + 5} \right){\rm{ }}\left( 3 \right)\)
Xét hàm số \(f\left( t \right) = 4{t^2} - 4t + 5,\forall t \in \left[ { - \frac{1}{2};1} \right].\) Ta có \(g'\left( t \right) = 8t - 4 = 0 \Leftrightarrow t = \frac{1}{2}.\)
\(g\left( { - \frac{1}{2}} \right) = 8,g\left( 1 \right) = 5,g\left( {\frac{1}{2}} \right) = 4.\) Do đó \(\mathop {\min }\limits_{\left[ { - \frac{1}{2};1} \right]} g\left( t \right) = 4.\) Nên \(\left( 3 \right) \Leftrightarrow m < 4.\)
Vậy \(m \in \left( {\frac{7}{4};4} \right)\) thỏa mãn yêu cầu bài toán.
Đáp án C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều và \(A'A = A'B = A'C.\) Biết rằng các cạnh bên của lăng trụ tạo với đáy một góc \({60^0}\) và khoảng cách giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {BCC'B'} \right)\) bằng 1. Tính thể tích khối lăng trụ đã cho.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có \(f'\left( x \right) = {\left( {x + 2} \right)^2}{\left( {x - 2} \right)^3}\left( { - x + 5} \right).\) Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
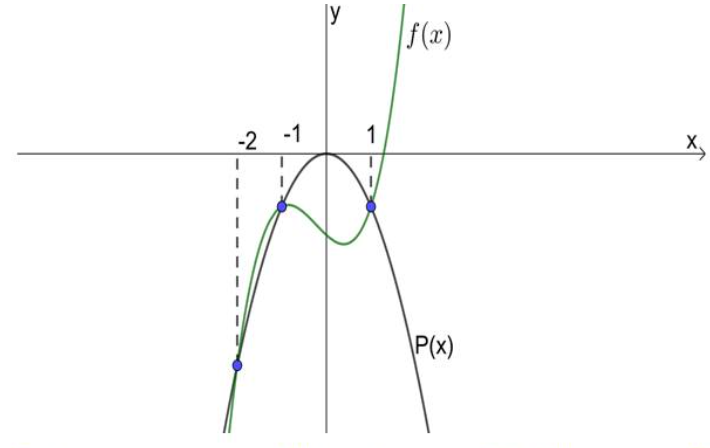
Cho parabol \(\left( P \right):y = - {x^2}\) và đồ thị hàm số \(y = a{x^3} + b{x^2} + cx - 2\) có đồ thị như hình vẽ. Tính giá trị của biểu thức \(P = a - 3b - 5c.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có \(AB = a;BC = 2a.\) Hai mặt phẳng \(\left( {SAB} \right)\) và mặt phẳng \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng đáy, cạnh \(SC\) hợp với mặt đáy góc \({60^0}.\) Tính thể tích khối chóp \(S.ABCD\) theo \(a.\)
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có đạo hàm \(f'\left( x \right) = {x^3}{\left( {x - 1} \right)^2}\left( {x + 2} \right).\) Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Cho biểu thức \(P = \sqrt[4]{{x\sqrt[3]{{{x^2}.\sqrt[3]{x}}}}},x >0.\) Mệnh đề nào dưới đây là đúng?
Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật với cạnh \(AD = 2CD.\) Biết hai mặt \(\left( {SAC} \right),\left( {SBD} \right)\) cùng vuông góc với mặt đáy và đoạn \(BD = 6;\) góc giữa \(\left( {SCD} \right)\) và mặt đáy bằng \({60^0}.\) Hai điểm \(M,N\) lần lượt là trung điểm của \(SA,SB.\) Thể tích khối đa diện \(ABCDMN\) bằng
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\) với \(AD = DC = a,AB = 2a.\) Hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\)cùng vuông góc với đáy. Góc giữa \(SC\) và mặt đáy bằng \({60^0}.\) Tính khoảng cách giữa hai đường thẳng \(AC\) và \(SB.\)
Cho mặt nón tròn xoay đỉnh \(S\) đáy là đường tròn tâm \(O\) có thiết diện qua trục là một tam giác đều cạnh bằng \(a.{\rm{ }}A,B\) là hai điểm bất kì trên đường tròn \(\left( O \right).\) Thể tích khối chóp \(S.OAB\) đạt giá trị lớn nhất bằng
Cho hàm số \(f\left( x \right)\) có đại hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} - 4x} \right)\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {2{x^2} - 12x + m} \right)\) có đúng 5 điểm cực trị?
Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {m - 1} \right){x^3} - 3\left( {m - 1} \right){x^2} + 3x + 2\) đồng biến trên \(\mathbb{R}.\)
Cho hàm số \(y = f\left( x \right)\). Đồ thị của hàm số \(y = f'\left( x \right)\) như hình bên.
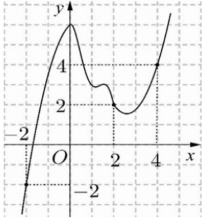
Đặt \(h\left( x \right) = f\left( x \right) - \frac{{{x^2}}}{2}.\) Mệnh đề nào dưới đây đúng?
Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = {x^3} - 3{x^2} - mx + 4\) có hai điểm cực trị thuộc khoảng \(\left( { - 3;3} \right)?\)
Anh Minh muốn xây dựng một hố ga không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được \(3200c{m^3}\), tỉ số giữa chiều cao và chiều rộng của hố ga bằng 2 . Xác định diện tích đáy của hố ga để khi xây hố tiết kiệm được nguyên vật liệu nhất.
Cho tứ diện \(ABCD\) có độ dài cạnh bằng \(a,\left( S \right)\) là mặt tiếp xúc với sáu cạnh của tứ diện \(ABCD.M\) là một điểm thay đổi trên \(\left( S \right).\) Tính tổng \(T = M{A^2} + M{B^2} + M{C^2} + M{D^2}.\)
