Một người gửi 200 triệu đồng vào ngân hàng với lãi suất 0,3% một tháng. Biết rằng nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đều để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng người đó thu được (cả số tiền gửi ban đầu và số tiền lãi) hơn 225 triệu đồng? (Giả định trong khoảng thời gan này lãi suất không thay đổi và người đó không rút tiền ra).

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 .$ Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng

Đường cong ở hình dưới đây là đồ thị của hàm số $y = \frac{{x + a}}{{bx + c}},\left( {a,b,c \in \mathbb{Z}} \right).$ Khi đó giá trị biểu thức $T = a - 3b - 2c$ bằng 

Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{{\sqrt {x + 4} - 2}}{{{x^2} - x}}$ là 

Cho hàm số $y = - {x^3} - 3\left( {m + 1} \right){x^2} + 3\left( {2m - 1} \right)x + 2020.$ Có bao nhiêu giá trị nguyên $m$ để hàm số nghịch biến trên $\left( { - \infty ; + \infty } \right)?$ 

Cho hàm số $f\left( x \right),$ bảng xét dấu của $f'\left( x \right)$ như sau:

  Hàm số $y = f\left( {1 - 2x} \right)$ nghịch biến trên khoảng nào dưới đây?

Hình bát diện đều có bao nhiêu cạnh? 

Cho lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A,AB = a\sqrt 3 ,AC = a.$ Điểm $A'$ cách đều ba điểm $A,B,C.$ Góc giữa đường thẳng $AB'$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^0}.$ Khoảng cách giữa hai đường thẳng $AA'$ và $BC$ bằng

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,BC = 2a,BA = a\sqrt 3 .$ Biết tam giác $SAB$ vuông tại $A,$ tam giác $SBC$ cân tại $S,\left( {SAB} \right)$ tạo với mặt phẳng $\left( {SBC} \right)$ một góc $\varphi$ thỏa mãn $\sin \varphi = \sqrt {\frac{{20}}{{21}}} .$ Thể tích của khối chóp $S.ABC$ bằng

Phương trình tiệm cận ngang của đồ thị hàm số $y = \frac{{4 - 3x}}{{4x + 5}}$ là 

Cho $x,y,z$ là ba số dương lập thành cấp số nhân; còn ${\log _a}x;{\log _{\sqrt a }}y;{\log _{\sqrt[3]{a}}}z$ lập thành cấp số cộng. Tính giá trị của biểu thức $Q = \frac{{2017x}}{y} + \frac{{2y}}{z} + \frac{z}{x}.$

Gọi $S$ là tập hợp các số tự nhiên có bốn chữ số đôi một khác nhau lập từ các số $0;1;2;3;4;5;6;7.$ Chọn ngẫu nhiên 1 số từ tập hợp $S.$ Tính xác suất để số được chọn có đúng 2 chữ số chẵn.

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

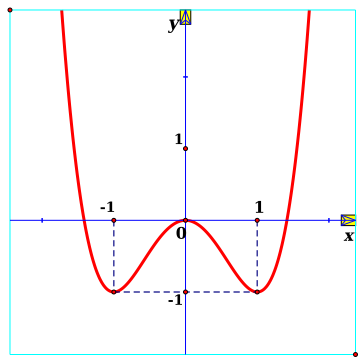
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ:

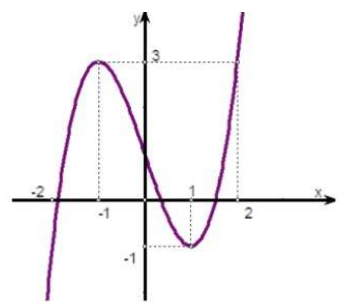
Gọi $S$ là tập các giá trị nguyên của tham số $m$ để phương trình $f\left( {4\left| {\sin x} \right| + m} \right) - 3 = 0$ có đúng 12 nghiệm phân biệt thuộc nửa khoảng $\left( {0;4\pi } \right].$ Tổng các phần tử của $S$ bằng

Đội văn nghệ của lớp 12A có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn ra 2 học sinh của đội văn nghệ sao cho 2 học sinh có 1 học sinh nam và 1 học sinh nữ.

Cho hàm số $y = \frac{{mx - 18}}{{x - 2m}}.$ Gọi $S$ là tập hợp các giá trị nguyên của tham số $m$ để hàm số đồng biến trên khoảng $\left( {2; + \infty } \right).$ Tổng các phần tử của $S$ bằng