Cho hai hàm số \(y = {2^x}\) và \(y = {\log _2}x\) lần lượt có đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\) Gọi \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) là hai điểm lần lượt thuộc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) sao cho tam giác \(IAB\) vuông cân tại \(I,\) trong đó \(I\left( { - 1; - 1} \right).\) Giá trị của \(P = \frac{{{x_A} + {y_A}}}{{{x_B} + {y_B}}}\) bằng
A.1
B.\( - 2.\)
C.3
D.\( - \frac{1}{2}.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
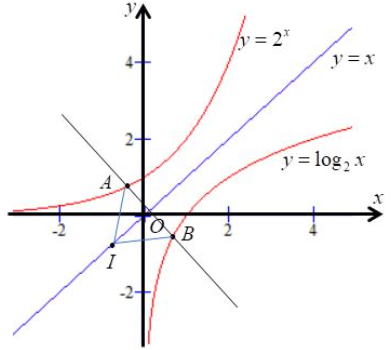
Ta có đồ thị hai hàm số \(y = {2^x}\) và \(y = {\log _2}x\) có đồ thị đối xứng với nhau qua đường thẳng \(d:y = x\) và \(I \in d.\)
Gọi \(M\) là trung điểm của \(AB,\) suy ra: \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M} \Rightarrow P = \frac{{{x_A} + {x_B}}}{{{y_A} + {y_B}}} = \frac{{{x_M}}}{{{y_M}}}.\end{array} \right.\)
Theo giả thiết tam giác \(IAB\) vuông cân tại \(I\) nên trung điểm \(M\) của \(AB\) thuộc đường thẳng \(d,\) suy ra \({y_M} = {x_M}.\) Vậy \(P = \frac{{{x_M}}}{{{y_M}}} = 1.\)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
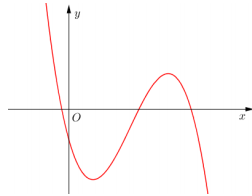
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) đồ thị là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
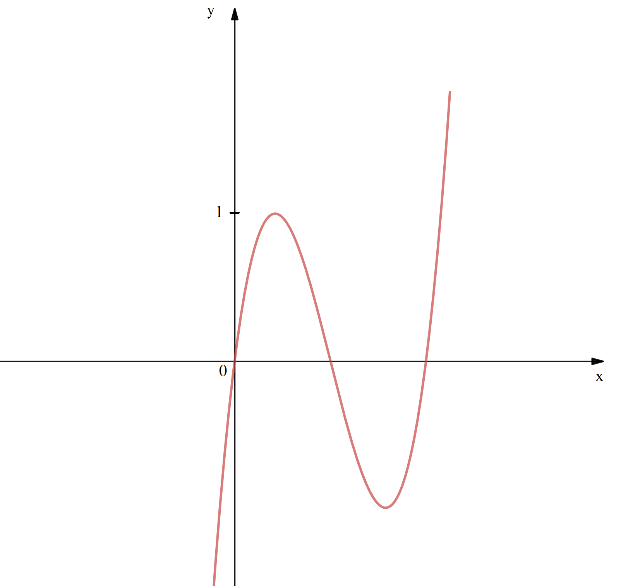
Cho hàm số \[f(x)\] có \[f(0) = 0\]. Biết rằng \[y = f'(x)\] là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \[g(x) = f(f(x) - x)\] có bao nhiêu điểm cực trị ?
Trong các hàm số dưới đây, hàm số nào nghịch biến trên khoảng \(\mathbb{R}?\)
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
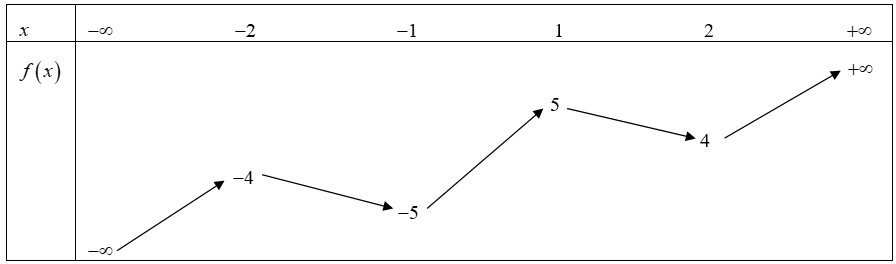
Có bao nhiêu giá trị nguyên của tham số \(m\) để trên đoạn \(\left[ { - 1;2} \right]\) phương trình \(3f\left( {{x^2} - 2x - 1} \right) = m\) có đúng hai nghiệm thực phân biệt?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
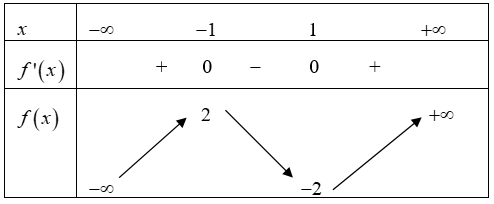
Số nghiệm thực của phương trình \(3f\left( x \right) + 1 = 0\) là
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng
Biết rằng giá trị lớn nhất của hàm số \(y = \frac{{\cos x + m}}{{2 - \cos x}}\) trên đoạn \(\left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right]\) bằng 1. Mệnh đề nào sau đây đúng?