Cho 2∫0f(x)dx=3 và 2∫0g(x)dx=7, khi đó 2∫0[f(x)+3g(x)]dx bằng
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Sử dụng tính chất tích phân: b∫a[f(x)+g(x)]dx=b∫af(x)dx+b∫ag(x)dx,b∫akf(x)dx=kb∫af(x)dx(k≠0).
Cách giải:
2∫0[f(x)+3g(x)]dx=2∫0f(x)dx+32∫0g(x)dx=3+3.7=24.
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình (S):x2+y2+z2−2x−4y−6z+5=0. Tính diện tích mặt cầu (S)
Đường tiệm cận đứng của đồ thị hàm số y=−3x+1x−1 có phương trình là:
Biết hàm số f(x) - f(2x) có đạo hàm bằng 20 tại x = 1 và đạo hàm bằng 1001 tại x = 2. Tính đạo hàm của hàm số
f(x) - f(4x) tại x = 1.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng φ và sinφ=√55. Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
Cho hàm số y = f(x) có bảng biến thiên như sau:
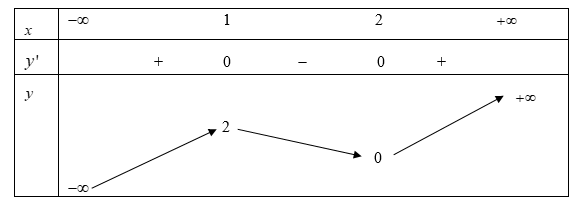
Số nghiệm thực của phương trình 2f(x)−3=0 là
Một khối trụ có diện tích xung quanh bằng 80π. Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10.
Cho tập hợp A={1;2;3;4;5;6;7;8}. Từ tập hợp A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho các số này lẻ và không chia hết cho 5?