A.
B. 25
C. 50
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
Đặt
Do là số thuần ảo nên (với
Ta có
Mặt khác theo bài ra thì nên ta có
Do A, B lần lượt là các điểm biểu diễn nên
Khi đó
Suy ra diện tích tam giác AOB là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phương trình Hỏi có bao nhiêu cặp thỏa mãn phương trình đã cho
Cho hàm số f(x) có bảng biến thiên như sau
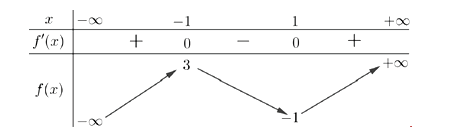
Số nghiệm của phương trình 3f(x) - 2 = 0 là
Cho phương trình (m là tam số thực). Số giá trị nguyên của m để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng (0; 1)
Trong không gian Oxyz, cho ba điểm Tọa độ trọng tâm của tam giác ABC là:
Cho năm số thực a < b < c < d < e. Hàm số y = f(x) xác định và liên tục trên đoạn [a; e] và đồ thị hàm số y = f(x) như hình vẽ:
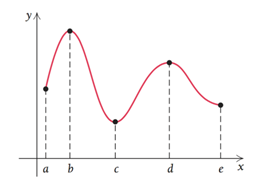
Đồ thị hàm số y = f(x) có bao nhiêu điểm cực tiểu?
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại C, biết AA' = 2a. Thể tích của khối lăng trụ đã cho bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh Thể tích khối chóp S.ABCD bằng