Trong không gian Oxyz, cho điểm A(0; 4; -3). Xét mặt phẳng (P) thay đổi cách điểm B(4; 0; -1) một khoảng bằng 3. Khi khoảng cách từ A đến (P) lớn nhất, (P) đi qua điểm nào dưới đây?
A. M(0;−3;10)
B. P(−3;0;−3).
C. N(0;3;−5).
D. Q(0;5;8).
Giải bởi Vietjack
Chọn A.
Ta có →AB(4;−4;2)⇒AB=√42+(−4)2+22=6.
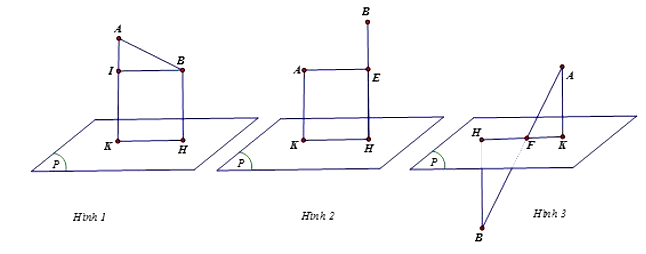
Trường hợp 1: Hai điểm A, B nằm cùng phía so với (P) có hai hình vẽ biểu diễn là hình 1 và hình 2.
Từ hình vẽ 1 ta có d(A,(P))=AK,d(B;(P))=BH=3.
AK=AI+IK≤AB+BH=6+3=9 (do IK=BH,AI≤AB).
Suy ra AK lớn nhất bằng 9 khi AI = AB điều này xảy ra khi A, B, H thẳng hàng và H = K.
Vậy d(A, (P)) lớn nhất bằng 9 và (P) nhận →AB(4;−4;2) làm véc tơ pháp tuyến.
Mặt phẳng (P) nhận →n(2;−2;1) là véc tơ pháp tuyến có phương trình dạng 2x−2y+z+D=0.
d(A,(P))=9⇔|D−11|3=9⇔[D=38D=−16.
Vậy (P) có phương trình 2x−2y+z+38=0 và 2x−2y+z−16=0.
Đối chiếu các phương án ta thấy có phương án A thỏa mãn.
Từ hình vẽ ta có d(A,(P))=AH=EH<BK=3<9 nên loại.
Trường hợp 2: Hai điểm A, B nằm khác phía so với (P).
Từ hình vẽ 3 ta có d(A,(P))=AK<AF<AB=6<9 nên loại.
Vậy đáp án là phương án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phương trình log3(3x2−6x+6)=3y2+y2−x2+2x−1. Hỏi có bao nhiêu cặp (x;y);0<x<2021;y∈ℕ thỏa mãn phương trình đã cho
Cho hàm số f(x) có bảng biến thiên như sau
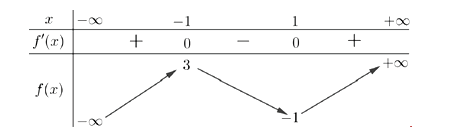
Số nghiệm của phương trình 3f(x) - 2 = 0 là
Cho phương trình log233x+log3x+m−1=0 (m là tam số thực). Số giá trị nguyên của m để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng (0; 1)
Trong không gian Oxyz, cho ba điểm A(−1;0;3),B(−3;2;−1),C(−2;1;1). Tọa độ trọng tâm của tam giác ABC là:
Cho năm số thực a < b < c < d < e. Hàm số y = f(x) xác định và liên tục trên đoạn [a; e] và đồ thị hàm số y = f(x) như hình vẽ:
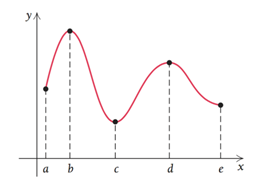
Đồ thị hàm số y = f(x) có bao nhiêu điểm cực tiểu?
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại C, biết AB=2a,AC=a, AA' = 2a. Thể tích của khối lăng trụ đã cho bằng
