Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu và Gọi M là điểm thay đổi, thuộc mặt cầu sao cho tồn tại ba mặt phẳng đi qua M, đôi một vuông góc với nhau và lần lượt cắt mặt cầu theo ba đường tròn. Giá trị lớn nhất của tổng chu vi ba đường tròn đó là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
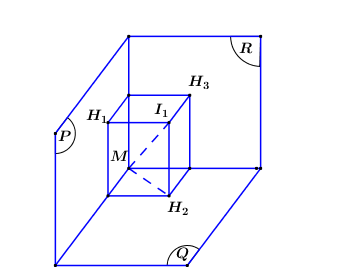
Mặt cầu có tâm , bán kính
Mặt cầu có tâm , bán kính
Ta có:
tiếp xúc ngoài.
Gọi là 3 mặt phẳng đi qua M đôi một vuông góc với nhau và lần lượt cắt mặt cầu theo ba đường tròn.
Gọi theo thứ tự là hình chiếu vuông góc của lên
theo thứ tự là bán kính các đường tròn tâm
Khi đó ta có
Tổng chu vi 3 đường tròn là:
Áp dụng BĐT Bunhiacopxki ta có:
Vậy Dấu “=” xảy ra khi
Chọn B.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số y = f(x) liên tục trên có bảng biến thiên như sau:
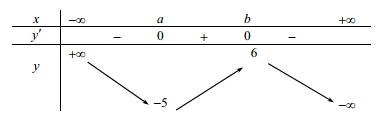
Đặt (m là tham số). Có bao nhiêu giá trị nguyên của m sao cho hàm số y = h(x) có đúng 5 điểm cực trị?
Trong không gian với hệ tọa độ Oxyz, đường thẳng đi qua hai điểm A(3; 1; -6) và B(5; 3; -2) có phương trình tham số là:
Có bao nhiêu giá trị nguyên của tham số m sao cho với mỗi giá trị của m bất phương trình nghiệm đúng với mọi giá trị x thuộc đoạn [0; 3]?
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm và Phương trình mặt phẳng song song với mặt phẳng (ABC) và đi qua điểm M là:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B. Biết thể tích khối lăng trụ ABC.A'B'C' bằng:
Cho hình nón (T) đỉnh S có đáy là đường tròn tâm O bán kính bằng 2, chiều cao hình nón (T) bằng 2. Khi cắt hình nón (T) bởi mặt phẳng đi qua trung điểm của đoạn SO và song song với đáy của hình nón, ta được đường tròn tâm I. Lấy hai điểm A và B lần lượt trên hai đường tròn và sao cho góc giữa và là Thể tích của khối tứ diện IAOB bằng:
Trong không gian với hệ tọa độ Oxyz, gọi G(a; b; c) là trọng tâm của tam giác ABC với và
C(2; 9; 0). Giá trị của tổng a + b + c bằng: