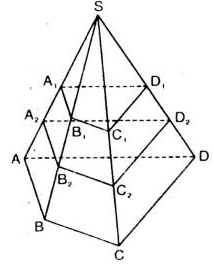
Cho hình chóp S. ABCD. Gọi A1 là trung điểm của cạnh SA và A2 là trung điểm của đoạn AA1. Gọi và là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A1, A2. Mặt phẳng cắt các cạnh SB, SC, SD lần lượt tại B1, C1, D1 . Mặt phẳng cắt các cạnh SB, SC, SD lần lượt tại B2, C2, D2. Chứng minh:
a) B1, C1, D1 lần lượt là trung điểm của các cạnh SB, SC, SD.
b) B1B2 = B2B, C1C2 = C2C, D1D2 = D2D.
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Chứng minh B1, C1, D1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
⇒A1B1 là đường trung bình của tam giác SAB.
⇒ B1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C1 là trung điểm của SC.
• D1 là trung điểm của SD.
b) Chứng minh B1B2 = B2B, C1C2 = C2C, D1D2 = D2D.
⇒A2B2 là đường trung bình của hình thang A1B1BA
⇒ B2 là trung điểm của B1B
⇒ B1B2 = B2B (đpcm)
*Chứng minh tương tự ta cũng được:
• C2 là trung điểm của C1C2 ⇒ C1C2 = C2C
• D2 là trung điểm của D1D2 ⇒ D1D2 = D2D.
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A1B1C1D1.ABCD và A2B2C2D2.ABCD
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình hộp ABCD.A’B’C’D’.
a) Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.
b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.
c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.
d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.
a) Chứng minh rằng AM song song với A’M’.
b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
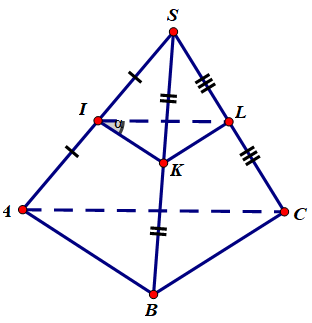
Cho tứ diện SABC. Hãy dựng mặt phẳng qua trung điểm I của đoạn SA và song song với mặt phẳng (ABC).
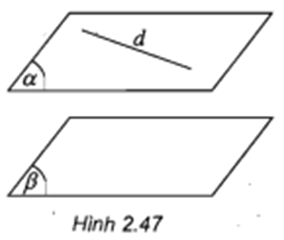
Cho hai mặt phẳng song song và . Đường thẳng d nằm trong α (h.2.47). Hỏi d và có điểm chung không?
Trong mặt phẳng cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên Trên a, b và c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.
a) Hãy xác định giao điểm D’ của đường thẳng d với mặt phẳng (A’B’C’).
b) Chứng minh A’B’C’D’ là hình bình hành.