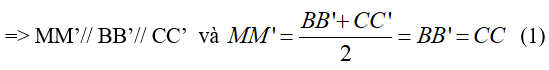7 câu hỏi trắc nghiệm thuộc Bài 4: Hai mặt phẳng song song

Câu 1:

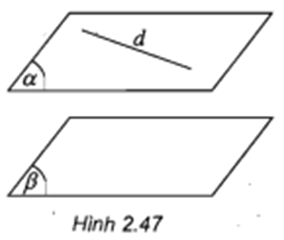
Cho hai mặt phẳng song song $α$ và $β$ . Đường thẳng d nằm trong α (h.2.47). Hỏi d và $β$ có điểm chung không?

Hai mặt phẳng song song α và $β \Rightarrow$ α và $β$ không có điểm chung

Đường thẳng d nằm trong $α \Rightarrow$ Đường thẳng d không thể cắt mặt phẳng $β$ . Vì nếu d cắt mặt phẳng $β$ tức là d và $β$ có điểm chung

$\Rightarrow$ hai mặt phẳng $α$ và $β$ có điểm chung (mâu thuẫn với giả thiết)

Vậy d và β không có điểm chung

Câu 2:

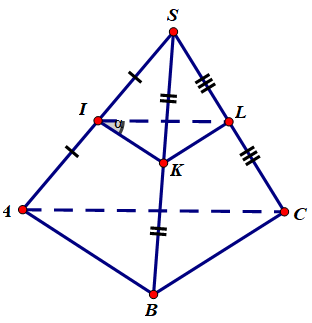
Cho tứ diện SABC. Hãy dựng mặt phẳng $(α)$ qua trung điểm I của đoạn SA và song song với mặt phẳng (ABC).

Xem đáp án

Mặt phẳng (α) là mặt phẳng đi qua 3 trung điểm I, K, L của SA, SB, SC

Thật vậy, do I, K , L lần lượt là trung điểm của SA, SB, SC nên IK, KL lần lượt là đường trung bình trong tam giác SAB và SBC

$I K // A B \in (A B C) \Rightarrow I K // (A B C)$

$K L / / B C \in (A B C) \Rightarrow K L / / (A B C)$

IK và KL cắt nhau và cùng // (ABC)

⇒ Mặt phẳng chứa IK và $K L / / (A B C)$ hay $(α) / / (A B C)$

Câu 3:

Phát biểu định lý Ta-lét trong hình học phẳng.

Xem đáp án

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ

Câu 4:

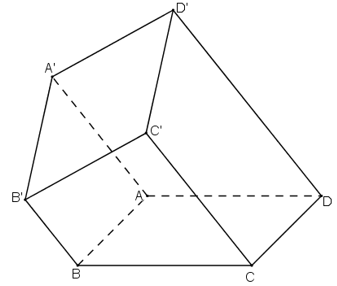
Trong mặt phẳng $(α)$ cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên $(α) .$ Trên a, b và c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.

a) Hãy xác định giao điểm D’ của đường thẳng d với mặt phẳng (A’B’C’).

b) Chứng minh A’B’C’D’ là hình bình hành.

Xem đáp án

a) Giả sử $(A ’ B ’ C ’) \cap d = D ’$

$\Rightarrow (A ’ B ’ C ’) \cap (C ’ C D) = C ’ D ’ .$

+ $A A ’ / / C C ’ \subset (C ’ C D)$

$\Rightarrow A A ’ / / (C ’ C D) .$

$A B / / C D \subset (C C ’ D)$

$\Rightarrow A B / / (C C ’ D)$

Câu 5:

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.

a) Chứng minh rằng AM song song với A’M’.

b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.

c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).

d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.

Xem đáp án

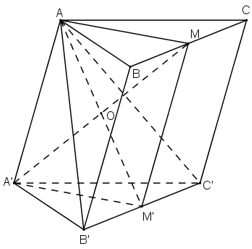
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành

Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình

Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)

Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’

=> Tứ giác AMM’A’ là hình bình hành

b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :

Ta có : O ∈ AM’ ⊂ (AB’C’)

⇒ O = A’M ∩ (AB’C’).

c)

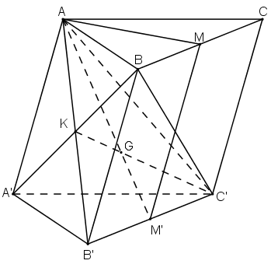
Gọi K = AB’ ∩ BA’, ta có :

K ∈ AB’ ⊂ (AB’C’)

K ∈ BA’ ⊂ (BA’C’)

⇒ K ∈ (AB’C’) ∩ (BA’C’)

Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)

⇒ (AB’C’) ∩ (BA’C’) = KC’.

Vậy d cần tìm là đường thẳng KC’

d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.

Ta có: G ∈ AM’ ⊂ (AM’M)

G ∈ C’K.

⇒ G = (AM’M) ∩ C’K.

+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’

⇒ K là trung điểm AB’.

ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K

⇒ G là trọng tâm ΔAB’C’.

Câu 6:

Cho hình hộp ABCD.A’B’C’D’.

a) Chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.

b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.

c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.

d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và AA’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.

Xem đáp án

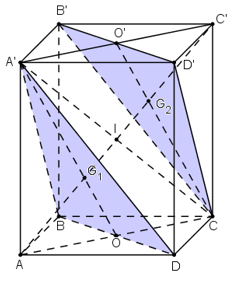
a) + A’D’ // BC và A’D’ = BC

⇒ A’D’CB là hình bình hành

⇒ A’B // D’C, mà D’C ⊂ (B’D’C) ⇒ A’B // (B’D’C) (1)

+ BB’ // DD’ và BB’ = DD’

⇒ BDD’B’ là hình bình hành

⇒ BD // B’D’, mà B’D’ ⊂ (B’D’C) ⇒ BD // (B’D’C) (2)

A’B ⊂ (BDA’) và BD ⊂ (BDA’); A’B ∩ BD = B (3)

Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C).

b) Gọi O = AC ∩ BD

+ Ta có: O ∈ AC ⊂ (AA’C’C)

⇒ A’O ⊂ (AA’C’C).

Trong (AA’C’C), gọi A’O ∩ AC’ = G₁.

G₁ ∈ A’O ⊂ (A’BD)

⇒ G₁ ∈ AC’ ∩ (BDA’).

+ Trong hình bình hành AA’C’C gọi I = A’C ∩ AC’

⇒ A’I = IC.

⇒ AI là trung tuyến của ΔA’AC

⇒ G1 = A’O ∩ AC’ là giao của hai trung tuyến AI và A’O của ΔA’AC

⇒ G1 là trọng tâm ΔA’AC

⇒ A’G1 = 2.A’O/3

⇒ G1 cũng là trọng tâm ΔA’BD.

Vậy AC' đi qua trọng tâm G₁ của ΔA’BD.

Chứng minh tương tự đối với điểm G₂.

c) *Vì G₁ là trọng tâm của ΔAA’C nên AG₁/AI = 2/3 .

Vì I là trung điểm của AC’ nên AI = 1/2.AC’

Từ các kết quả này, ta có : AG1 = 1/3.AC’

*Chứng minh tương tự ta có : C’G2 = 1/3.AC’

Suy ra : AG₁ = G₁G₂ = G₂C’ = 1/3.AC’.

d) (A’IO) chính là mp (AA’C’C) nên thiết diện cần tìm chính là hình bình hành AA’C’C.

Câu 7:

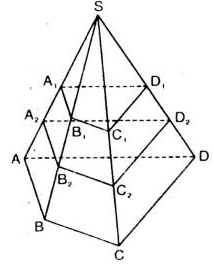
Cho hình chóp S. ABCD. Gọi A₁ là trung điểm của cạnh SA và A₂ là trung điểm của đoạn AA₁. Gọi $(α)$ và $(β)$ là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A₁, A₂. Mặt phẳng $(α)$ cắt các cạnh SB, SC, SD lần lượt tại B₁, C₁, D₁ . Mặt phẳng $(β)$ cắt các cạnh SB, SC, SD lần lượt tại B₂, C₂, D₂. Chứng minh:

a) B₁, C₁, D₁ lần lượt là trung điểm của các cạnh SB, SC, SD.

b) B₁B₂ = B₂B, C₁C₂ = C₂C, D₁D₂ = D₂D.

c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.

Xem đáp án

a) Chứng minh B₁, C₁, D₁ lần lượt là trung điểm của các cạnh SB, SC, SD

Ta có:

$\begin{array}{l} (α) / / (ABCD) \\ (SAB) \cap (α) = A_{1} B_{1} \\ (SAB) \cap (ABCD) = AB \end{array}} \Rightarrow A_{1} B_{1} / / AB$

⇒A₁B₁ là đường trung bình của tam giác SAB.

⇒ B₁ là trung điểm của SB (đpcm)

*Chứng minh tương tự ta cũng được:

• C₁ là trung điểm của SC.

• D₁ là trung điểm của SD.

b) Chứng minh B₁B₂ = B₂B, C₁C₂ = C₂C, D₁D₂ = D₂D.

$\begin{array}{l} (α) / / (β) (vì cùng song song mp (ABCD)) \\ (SAB) \cap (α) = A_{1} B_{1} \\ (SAB) \cap (β) = A_{2} B_{2} \end{array}} \Rightarrow A_{1} B_{1} / / A_{2} B_{2}$

⇒A₂B₂ là đường trung bình của hình thang A₁B₁BA

⇒ B₂ là trung điểm của B₁B

⇒ B₁B₂ = B₂B (đpcm)

*Chứng minh tương tự ta cũng được:

• C₂ là trung điểm của C₁C₂ ⇒ C₁C₂ = C₂C

• D₂ là trung điểm của D₁D₂ ⇒ D₁D₂ = D₂D.

c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A₁B₁C₁D₁.ABCD và A₂B₂C₂D₂.ABCD

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 11 Hình học - Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

Bài 4: Hai mặt phẳng song song

Danh sách câu hỏi

Bài thi liên quan