Cho hình thoi ABCD có cạnh bằng 2 cm và \(\widehat {ABC} = 60^\circ \). Tìm khẳng định SAI trong các khẳng định sau?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A.
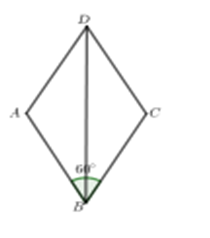
Vì \(\widehat {ABC} = 60^\circ \) nên \(\widehat {BAD} = 120^\circ \).
Ta có ABCD là hình thoi nên AB = AD = 2 cm.
Lại có BD là tia phân giác của góc \(\widehat {ABC}\) nên \(\widehat {ABD} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}.60^\circ = 30^\circ \).
Mà AB = AD nên tam giác ABD cân tại A.
Do đó: \(\widehat {ADB} = \widehat {ABD} = 30^\circ \) và \(\widehat {BAD} = 180^\circ - 2\widehat {ABD} = 180^\circ - 2.30^\circ = 120^\circ \).
Áp dụng định lí côsin trong tam giác ABD ta có:
\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {BAD}\)
Thay số: \(B{D^2} = {2^2} + {2^2} - 2.2.2.\cos 120^\circ = 12\)\( \Rightarrow BD = 2\sqrt 3 \)cm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tam giác ABC có b = 12, c = 15, \(\widehat A = 140^\circ \). Khi đó, tìm khẳng định sai trong các khẳng định dưới đây?
Cho tam giác ABC biết a = 3, b = 5, c = 7. Tìm khẳng định đúng trong các khẳng định sau?
Cho tam giác ABC biết AB = 3, \(AC = 3\sqrt 2 \) và \(\widehat C = 45^\circ \). Trong các phương án dưới đây, chọn phương án SAI?