Với giả thiết của bài tập 11, gọi N, P, Q lần lượt là giao của mặt phẳng với các đường thẳng CD,DS,SA. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
(A) Đường thẳng.
(B) Nửa đường thẳng.
(C) Đoạn thẳng song song với AB.
(D) Tập hợp rỗng.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
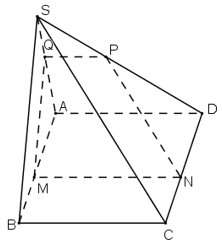
là đường thẳng qua S và song song với AB.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
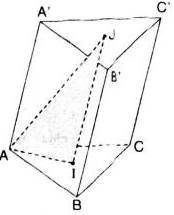
Cho tứ diện ABCD. Gọi I, J, K lần lượt là trung điểm của AC, BC và BD (hình bên). Giao tuyến của hai mặt phẳng (ABD) và (IJK) là
Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng song song với (SBC). Thiết diện tạo bởi và hình chóp S.ABCD là hình gì?
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I,J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là
Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó
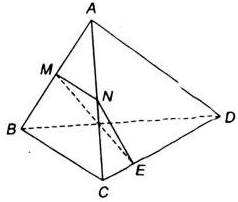
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC, E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo mặt phẳng (MNE) và tứ diện ABCD là:
Cho tứ diện đều S.ABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng song song với (SIC). Thiết diện tạo bởi và tứ diện S.ABC là
Cho hình bình hành ABCD. Gọi là các đường thẳng song song lần lượt với nhau đi qua B,C,D và nằm về một phía của mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt lần lượt tại B’,C’,D’ với Khi đó CC’ bằng