Số tiệm cận ngang của đồ thị hàm số là
A. 2
B. 1
C. 0
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
Phương pháp: Tính giới hạn để suy ra tiệm cận ngang.
Cách giải: Ta có:
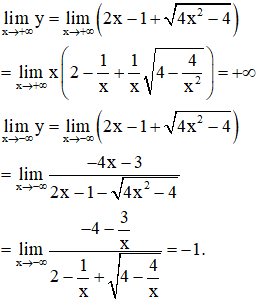
Vậy đồ thị hàm số có đúng một tiệm cận ngang y = 1.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
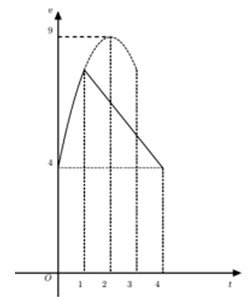
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t (h) có đồ thị vận tốc như hình vẽ. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;9) và có trục đối xứng song song với trục tung, khoảng thời gian còn lại vật chuyển động thẳng chậm dần đều. Tính quãng đường S mà vật di chuyển được trong 4 giờ đó (kết quả làm tròn đến hàng phần trăm).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây là sai?
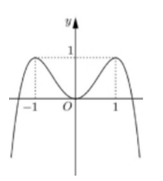
Đường cong trong hình bên là đồ thị của một trong bốn hàm số nào sau đây?
Cho hình chóp S.ABCD có các cạnh bên bằng a, góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng ( thay đổi). Tìm giá trị lớn nhất của thể tích của S.ABCD?
Cho hàm số f(x) và g(x) có đạo hàm trên [1;4] và thỏa mãn hệ thức sau với mọi
. Tính
Gọi S là tập hợp tất cả các nghiệm của phương trình trên đoạn . Số phần tử của S là.
Cho mặt cầu (S) bán kính . Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)(D không thuộc đường tròn (C) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
Xét các số phức thỏa mãn . Tính a-b biết biểu thức đạt giá trị nhỏ nhất.