Trong mặt phẳng Oxy, cho tam giác ABC với A(2; 4); B(3; 1); C(-1; 1).
a) Tìm tọa độ trọng tâm G, trực tâm H, tâm I của đường tròn ngoại tiếp tam giác ABC;
b) Chứng minh H, G, I thẳng hàng.
Giải bởi Vietjack
A(2;4), B(3;1), C( - 1;1)
a) Tọa độ trọng tâm G của tam giác ABC là:
Vậy G(4/3; 2)
Goi H(x; y), ta có:
H là trực tâm tam giác ABC
Gọi I(x; y), I là tâm đường tròn ngoại tiếp tam giác ABC ⇔ IA = IB = IC
Vậy: I(1; 2)
b) Ta có: 
⇒ 
cùng phương nên H, G, I thẳng hàng.
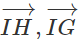
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện:
(a + b + c)(a + b - c) = 3ab. Khi đó số đo của góc C là:
Giải các tam giác ABC biết: góc A = 60ο; góc B = 40ο; cạnh c = 14
Cho góc x thỏa mãn điều kiện 90ο < x < 180ο. Khẳng định nào sau đây là đúng?
Tam giác ABC có góc B = 60ο, góc C = 45ο, BC = a. Tính độ dài hai cạnh AB và AC.
Tam giác ABC có góc A = 60ο, các cạnh b = 20, c = 35.
a) Tính chiều cao ha;
b) Tính bán kính đường tròn ngoại tiếp tam giác;
c) Tính bán kính đường tròn nội tiếp tam giác.
Tam giác đều nội tiếp đường tròn bán kính R = 4cm có diện tích là:
Tam giác ABC có BC = 12, CA = 13, trung tuyến AM = 8
a) Tính diện tích tam giác ABC;
b) Tính góc B.
Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Bán kính R bằng:
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Tích vô hướng bằng:
Cho tam giác ABC có diện tích S. Nếu tăng độ dài mỗi cạnh BC và AC lên hai lần đồng thời giữ nguyên độ lớn của góc C thì diện tích của tam giác mới được tạo nên là:
Tam giác ABC vuông và cân tại A có AB = a. Đường tròn nội tiếp tam giác ABC có bán kính r bằng:
Cho góc xOy = 30ο. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 2. Độ dài lớn nhất của đoạn OB bằng:
Tam giác ABC có AB = 8cm, BC = 10cm, CA = 6cm. Đường trung tuyến AM của tam giác có độ dài bằng:
