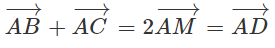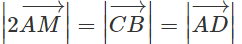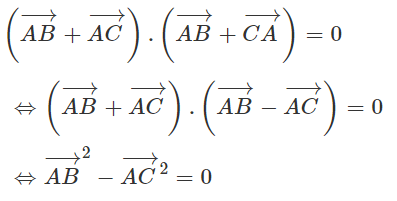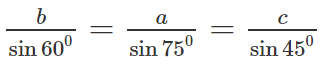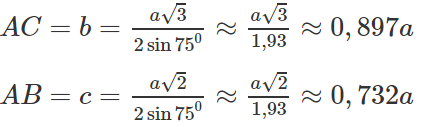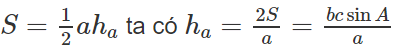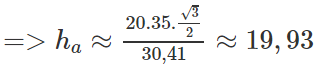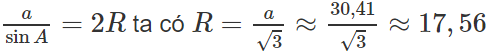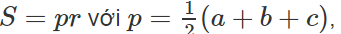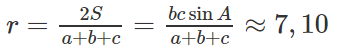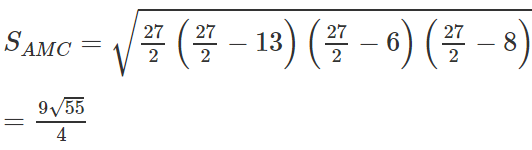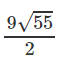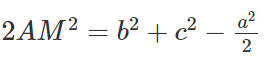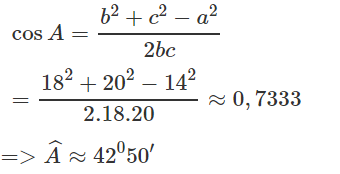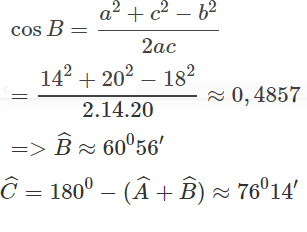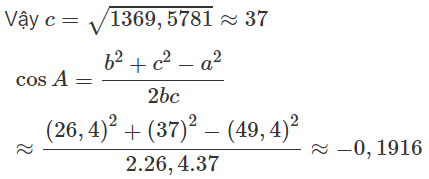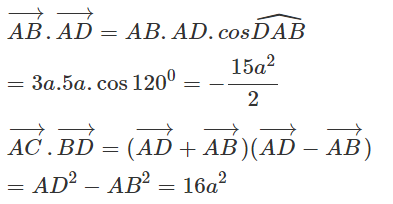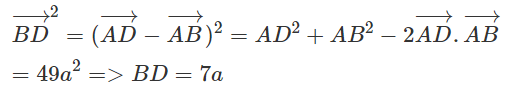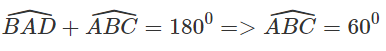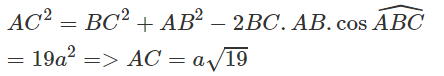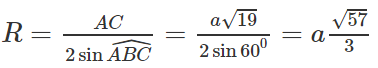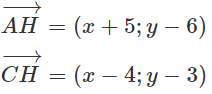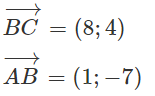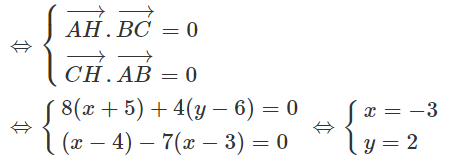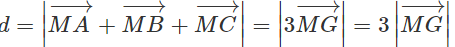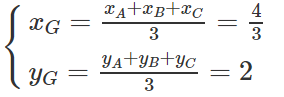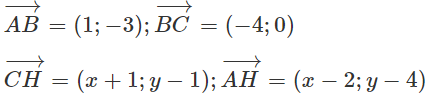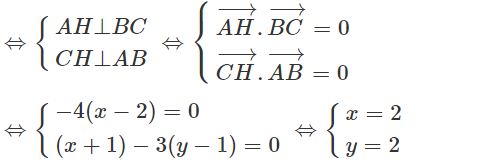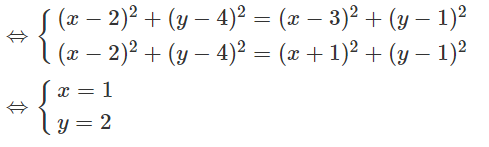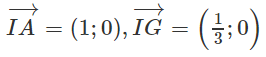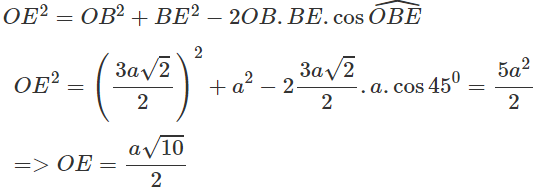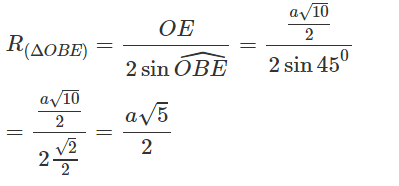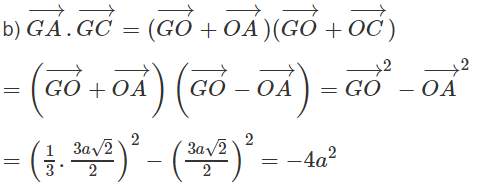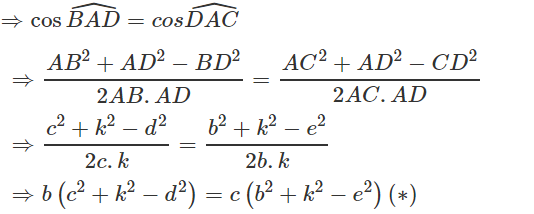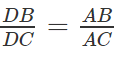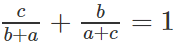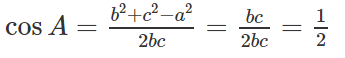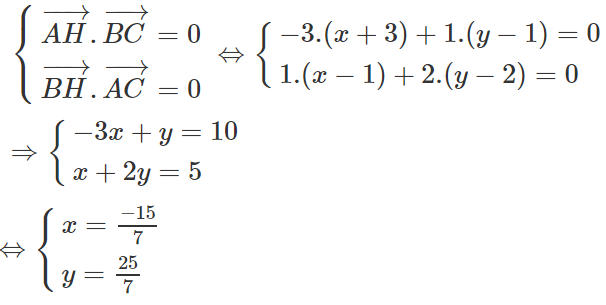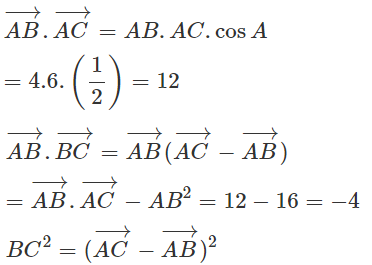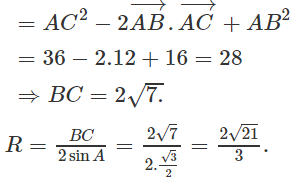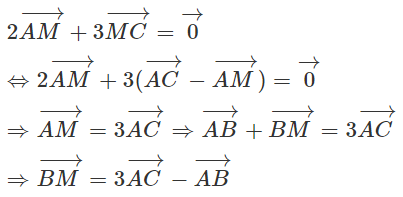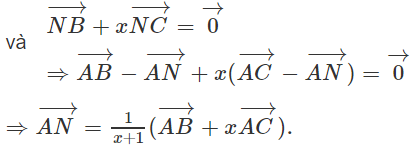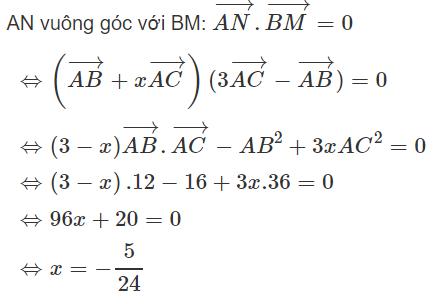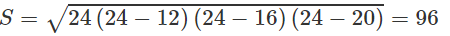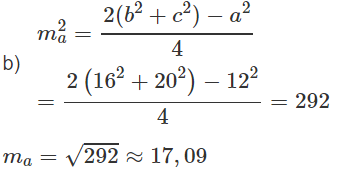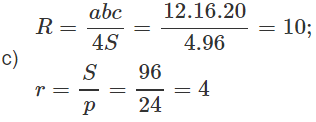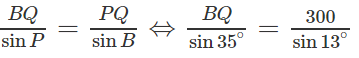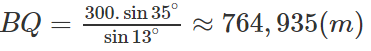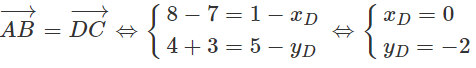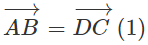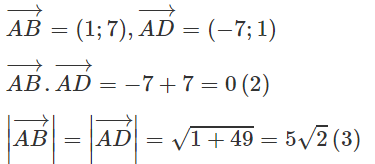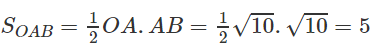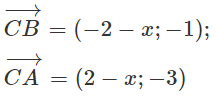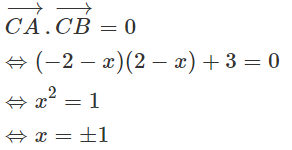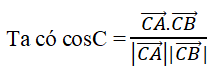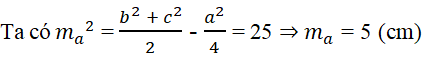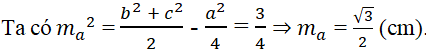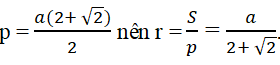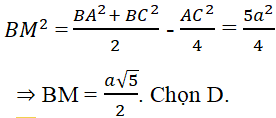53 câu hỏi trắc nghiệm thuộc Ôn tập chương 2 - SBT Hình học 10

Câu 1:

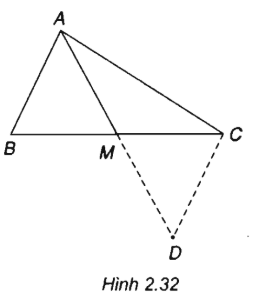
Cho tam giác ABC thỏa mãn điều kiện $|\vec{AB} + \vec{AC}| = |\vec{AB} - \vec{AC}|$ . Vậy tam giác ABC là tam giác gì?

Xem đáp án

(h.2.32)

Gọi M là trung điểm của cạnh BC ta có:

Mặt khác .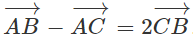

Theo giả thiết ta có:

Hay AM = BC/2

Ta suy ra ABC là tam giác vuông tại A.

Câu 2:

Ba điểm A, B, C phân biệt tạo nên vec tơ $\vec{AB} + \vec{AC}$ vuông góc với vec tơ $\vec{AB} + \vec{CA}$ . Vậy tam giác ABC là tam giác gì?

Xem đáp án

Theo giả thiết ta có:

Ta suy ra ABC là tam giác có AB = AC (tam giác cân tại A)

Câu 3:

Tính các cạnh còn lại của tam giác ABC trong mỗi trường hợp sau:

a) a = 7, b = 10, góc C = 56^ο29';

b) a = 2, c = 3, góc B = 123^ο17';

c) b = 0,4, c = 12, góc A = 23^ο28'

Xem đáp án

a) c² = a² + b² - 2ab.cosC = 49 + 100 - 140.cos56^ο29'

⇒c² ≈ 71,7 hay c ≈ 8,47

b) b ≈ 4,43

c) a ≈ 11,63

Câu 4:

Tam giác ABC có góc B = 60^ο, góc C = 45^ο, BC = a. Tính độ dài hai cạnh AB và AC.

Xem đáp án

Ta có: góc A = 180^ο - (60^ο + 45^ο) = 75^ο

Đặt AC = b, AB = a. Theo định lí sin:

Ta suy ra

Câu 5:

Tam giác ABC có góc A = 60^ο, các cạnh b = 20, c = 35.

a) Tính chiều cao h_a;

b) Tính bán kính đường tròn ngoại tiếp tam giác;

c) Tính bán kính đường tròn nội tiếp tam giác.

Xem đáp án

Ta có:

a² = b² + c² - 2bc.cosA = 20² + 35² - 20.35 = 925

Vậy a ≈ 30,41

a) Từ công thức

b) Từ công thức

c) Từ công thức

ta có:

Câu 6:

Cho tam giác ABC có BC = a, CA = b, AB = c. Chứng minh rằng: b² - c² = a(b.cosC - c.cosB)

Xem đáp án

Ta có: b² = a² + c² - 2ac.cosB

c² = a² + b² - 2ab.cosC

⇒ b² - c² = c² - b² + 2a(b.cosC - c.cosB)

⇒ 2(b² - c²) = 2a(b.cosC - c.cosB)

Hay b² - c² = a(b.cosC - c.cosB)

Câu 7:

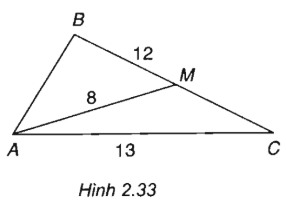
Tam giác ABC có BC = 12, CA = 13, trung tuyến AM = 8

a) Tính diện tích tam giác ABC;

b) Tính góc B.

Xem đáp án

(h.2.33)

Theo công thức Hê – rông ta có:

S_ABC = 2S_AMC =

Mặt khác ta có

hay

Do đó

Câu 8:

Giải tam giác ABC biết các cạnh: a = 14, b = 18, c = 20

Xem đáp án

Tam giác ABC có cạnh là BC = 14, CA = 18, AB = 20, ta cần tìm các góc A, B, C

Ta có:

Câu 9:

Giải các tam giác ABC biết: góc A = 60^ο; góc B = 40^ο; cạnh c = 14

Xem đáp án

Tam giác ABC có cạnh c = AB = 14 và có góc A = 60^ο; góc B = 40^ο.

Ta có: C = 180^ο - (A + B) = 80^ο cần tìm a và b.

Theo định lí sin:

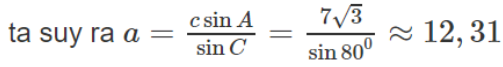
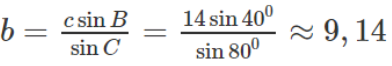
Câu 10:

Cho tam giác ABC có các cạnh a = 49,4; b = 26,4; góc C = 47^ο20'. Tính góc A, B và cạnh c

Xem đáp án

Theo định lí cô sin ta có:

c² = a² + b² - 2ab.cosC = (49,4)² + (26,4)² - 2. 49,4. 26,4.cos 47^ο20' ≈ 1369,5781

Ta suy ra góc A ≈ 101^ο3'

góc B ≈ 180^ο - (101^ο3' + 47^ο20') = 31^ο37'

Câu 11:

Cho hình bình hành ABCD có AB = 3a, AD = 5a, góc BAD bằng 120^ο

a) Tìm các tích vô hướng sau: $\vec{AB} . \vec{AD} . \vec{AC} . \vec{BD}$

b) Tính độ dài BD và bán kính đường tròn ngoại tiếp tam giác ABC.

Xem đáp án

a)

b)

ABCD là hình bình hành nên: BC = AD = 5a;

Áp dụng định lí hàm số cô sin trong tam giác ABC, ta được:

Áp dụng định lí hàm số sin trong tam giác ABC, ta được:

Câu 12:

Trong mặt phẳng Oxy, cho tam giác ABC với A(-5; 6), B(-4; -1), C(4; 3)

a) Tính tọa độ trực tâm H của tam giác ABC;

b) Tìm điểm M thuộc trục Oy sao cho $|\vec{MA} + \vec{MB} + \vec{MC}|$ ngắn nhất.

Xem đáp án

a) Gọi H(x; y). Ta có:

Và

H là trực tâm giác ABC

Vậy H(-3;2)

b) Vì M thuộc trục Oy nên M(O;y).

Gọi G là trọng tâm tam giác ABC, ta có tọa độ điểm G là 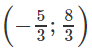và

d đạt giá trị nhỏ nhất ⇔ MG ⊥ Oy ⇔ y = y_G ⇔ y = 8/3

Vậy M(0; 8/3)

Câu 13:

Trong mặt phẳng Oxy, cho tam giác ABC với A(2; 4); B(3; 1); C(-1; 1).

a) Tìm tọa độ trọng tâm G, trực tâm H, tâm I của đường tròn ngoại tiếp tam giác ABC;

b) Chứng minh H, G, I thẳng hàng.

Xem đáp án

A(2;4), B(3;1), C( - 1;1)

a) Tọa độ trọng tâm G của tam giác ABC là:

Vậy G(4/3; 2)

Goi H(x; y), ta có:

H là trực tâm tam giác ABC

Gọi I(x; y), I là tâm đường tròn ngoại tiếp tam giác ABC ⇔ IA = IB = IC

Vậy: I(1; 2)

b) Ta có:

⇒ cùng phương nên H, G, I thẳng hàng.

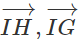
Câu 14:

Cho hình vuông ABCD có cạnh bằng 3a, tâm O; E là điểm trên cạnh BC và BE = a.

a) Tính cạnh OE và bán kính đường tròn ngoại tiếp tam giác OBE;

b) Gọi G là trọng tâm tam giác ACD. Tính tích vô hướng: $\vec{GA} . \vec{GC}$

Xem đáp án

a) Áp dụng định lí hàm số cô sin trong tam giác OBE ta được:

Áp dụng định lí hàm số sin trong tam giác OBE ta được:

Câu 15:

Cho tam giác ABC có AB = c, AC = b (với b ≠ c) phân giác trong AD = k (D nằm trên cạnh BC), BD = d, CD = e. Chứng minh hệ thức: k² = bc - de

Xem đáp án

Ta có AD là phân giác trong góc A của tam giác ABC nên góc BAD = góc DAC

Vì AD là phân giác trong góc A của tam ABC nên

⇒ bd = ce, từ (∗) ta suy ra (b - c)(-k² + bc - be) = 0

⇒ k² = bc - de (vì b ≠ c) (điều phải chứng minh)

Câu 16:

Cho tam giác ABC có BC = a, CA = b và AB = c thỏa mãn hệ thức $\frac{c}{b + a} + \frac{b}{a + c} = 1$ . Hãy tính số đo của góc A.

Xem đáp án

Ta có:

⇒ c(a + c) + b(b + a) = (b + a)(a + c)

⇒ ca + c² + b² + ba = ba + bc + a² + ac

⇒ b² + c² - a² = bc

Ta có:

⇒ góc A = 60^ο

Câu 17:

Trong mặt phẳng Oxy cho tam giác ABC có A(1; 2), B(-3; 1) và trực tâm H(-2; 3). Hãy tìm tọa độ đỉnh C.

Xem đáp án

A(1; 2), B(-3; 1) và trực tâm H(-2; 3).

Gọi C(x;y). Ta có:

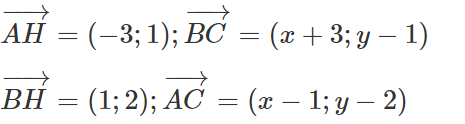
Câu 18:

Cho tam giác ABC góc BAC = 60^ο, AB = 4 và AC = 6.

a) Tính tích vô hướng $\vec{AB} . \vec{AC}, \vec{AB} . \vec{BC}$ , độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác ABC;

b) Lấy các điểm M, N định bởi:

$2 \vec{AM} + 3 \vec{MC} = \vec{0} và \vec{NB} + x \vec{NC} = \vec{0} (x \neq - 1)$

Định x để AN vuông góc với BM.

Xem đáp án

a)

b)

Câu 19:

Cho tam giác ABC có a = 12, b = 16, c = 20.

a)Tính diện tích S và chiều cao h_a của tam giác;

b)Tính độ dài đường trung tuyến m_a của tam giác;

c)Tính bán kính R và r của các đường tròn ngoại tiếp và nội tiếp tam giác.

Xem đáp án

a) Theo công thức Hê – rông với p = (12 + 16 + 20)/2 = 24

Ta có:

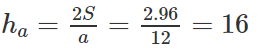
Câu 20:

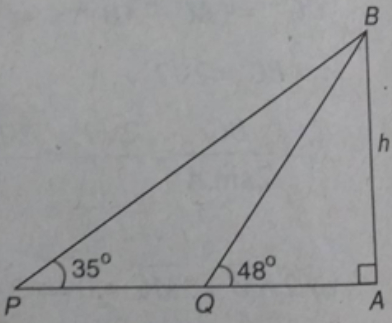
Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc BPA = 35^ο và BQA = 48^ο

a) Tính BQ;

b) Tính chiều cao của tháp.

Xem đáp án

a) (Xem hình 2.34)

Ta có: PBQ = 48^ο - 35^ο = 13^ο

Trong tam giác BPQ ta có:

Do đó:

b) Chiều cao của tháp là

AB = BQ.sin 48^ο

≈ 764,935.sin 48^ο ≈ 568,457

Câu 21:

Trong mặt phẳng tọa độ cho ba điểm A(7; -3), B(8; 4), C(1; 5).

a) Tìm tọa độ điểm D thỏa mãn $\vec{AB} = \vec{DC}$

b) Chứng minh rằng tứ giác ABCD là hình vuông.

Xem đáp án

a)

Vậy D(0;-2)

b) Ta có:

Từ (1), (2), (3) ⇒ ABCD là hình vuông.

Câu 22:

Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 3) và B(4; 2).

a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;

b) Tính chu vi tam giác OAB;

c) Tính diện tích tam giác OAB

Xem đáp án

a) Vì điểm D nằm trên Ox nên tọa độ của nó có dạng D(x;0)

Theo giả thiết DA = DB nên DA² = DB²

Do đó:

(1 - x)² + 3² = (4 - x)² + 2²

⇔ x² - 2x + 1 + 9 = 16 - 8x + x² + 4

⇔ x = 5/3

b) Gọi 2p là chu vi tam giác OAB, ta có:

2p = OA + OB + OC

c) Ta có : OA² + AB² = OB²

⇒ tam giác OAB vuông tại A

⇒

Vậy diện tích tam giác OAB là 5 (đvdt)

Câu 23:

Trên mặt phẳng tọa độ Oxy cho điểm A(2; -1)

a) Tìm tọa độ điểm B đối xứng với A qua gốc tọa độ O;

b) Tìm tọa độ điểm C có tung độ bằng 2 sao cho tam giác ABC vuông ở C.

Xem đáp án

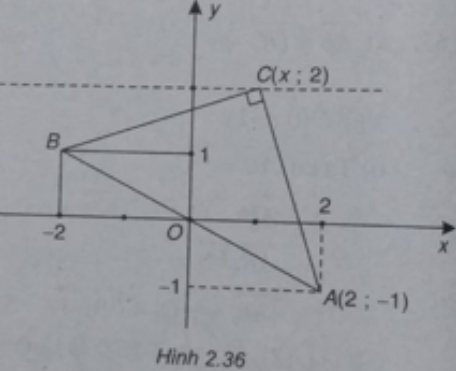
(Xem hình 2.36)

a) Ta có A(2; -1), tọa độ điểm B đối xứng với A qua O là B(-2; 1)

b) Ta có: C(x; 2), do đó:

Tam giác ABC vuông tại C nên

Vậy ta có hai điểm C(1;2) và (-1;2).

Câu 24:

Cho góc x thỏa mãn điều kiện 0^ο < x < 90^ο. Khẳng định nào sau đây là sai?

A. sin x > 0

B. cos x < 0

C. tan x > 0

D. cot x > 0

Xem đáp án

Khi 0^o < x < 90^o ta có sinx, cosx, tanx, cotx đều dương.

Đáp án: B

Câu 25:

Cho góc x thỏa mãn điều kiện 90^ο < x < 180^ο. Khẳng định nào sau đây là đúng?

A. cos x < 0

B. sin x < 0

C. tan x > 0

D. cot x > 0

Xem đáp án

Khi 90^o < x < 180^o, ta có sinx > 0, cosx < 0, tanx < 0, cotx < 0

Đáp án: A

Câu 26:

Giá trị của biểu thức m.sin0^ο + n.cos0^ο + p.sin90^ο

A. n - p

B. m + p

C. m - p

D. n + p

Xem đáp án

Ta có sin0^o = 0, cos0^o = 1, sin90^o = 1.

Đáp án: D

Câu 27:

Rút gọn biểu thức S = a²sin90^ο + b²cos90^ο + c²cos180^ο, ta có S bằng:

A. $a^{2} + b^{2}$

B. $a^{2} - b^{2}$

C. $a^{2} - c^{2}$

D. $b^{2} + c^{2}$

Xem đáp án

Ta có sin90^o = 1, cos90^o = 0, cos180^o = -1.

Đáp án: D

Câu 28:

Giá trị của biểu thức S = 3 - sin²90^ο + 2cos²60^ο - 3tan²45^ο bằng:

A. 0,5

B. -0,5

C. 1

D. 3

Xem đáp án

sin90^o = 1, cos60^o = 1/2, tan45^o = 1.

Đáp án: B

Câu 29:

Cho biểu thức P = 3sin²x + 4cos²x, biết cosx = 0,5, giá trị của P bằng bao nhiêu?

A. P = 7/4

B. P = 1/4

C. P = 7

D. P = 13/4

Xem đáp án

Ta có P = 3(1 - cos² x) + 4cos² x = 3 + cos²x = 3 + 1/4 = 13/4.

Đáp án: A

Câu 30:

Trong các khẳng định sau, khẳng định nào sai?

A. ${(sinx + cosx)}^{2}$ = 1 + 2sinxcosx

B. ${(sinx + cosx)}^{2}$ = 1 - 2sinxcosx

C. $\sin^{4} x + \cos^{4} x$ = 1 - 2.sin^2x.cos^2x

D. $\sin^{6} x + \cos^{6} x$ = 1 - sin^2x.cos^2x

Xem đáp án

Vì sin⁶x + cos⁶x = 1 - 3sin² x. cos²x

Đáp án: D

Câu 31:

Giá trị của biểu thức S = cos²12^ο + cos²78^ο + cos²1^ο + cos²89^ο bằng:

A. S = 0

B. S = 1

C. S = 2

D. S = 4

Xem đáp án

Vì 12^o + 78^o = 90^o nên cos78^o = sin12^o. Tương tự cos89^o = sin1^o.

Ta có S = cos² 12^o + sin² 12^o + cos² 1^o + sin² 1^o.

Đáp án: C

Câu 32:

Gọi G là trong tâm tam giác đều ABC có cạnh bằng a. Trong các khẳng định sau, khẳng định nào sai?

A. $\vec{AB} . \vec{AC} = \frac{1}{2} a^{2}$

B. $\vec{AB} . \vec{CB} = \frac{- 1}{2} a^{2}$

C. $\vec{GA} . \vec{GB} = \frac{a^{2}}{6}$

D. $\vec{AB} . \vec{AG} = \frac{1}{2} a^{2}$

Xem đáp án

GA = GB = 2/3.(a√3)/2 = (a√3)/3 và (GA→, GB→) = 120^o

Đáp án: C

Câu 33:

Cho hình vuông ABCD có cạnh bằng a. Tích vô hướng $\vec{AB} . \vec{AC}$ bằng bao nhiêu?

$A . a^{2}$

$B . \frac{a^{2}}{2}$

$C . 2 a^{2}$

$D . a^{2} \sqrt{2}$

Xem đáp án

AB→. AC→ = AB.AC.cos45^o = a.a√2.√2/2 = a².

Đáp án: A

Câu 34:

Cho hai vectơ a, b (khác vectơ 0) thỏa mãn: $\vec{a} . \vec{b} = - |\vec{a}| |\vec{b}|$ . Trong các khẳng định sau, khẳng định nào đúng:

A. $\vec{a} ⊥ \vec{b}$

B. $\vec{a} và \vec{b} cùng hướng$

C. $\vec{a} và \vec{b} ngược hướng$

D. $\vec{a} = - \vec{b}$

Xem đáp án

a→. b→ = -|a→|.|b→| ⇔ |a→|.|b→|. cos(a→, b→) = -|a→|.|b→| ⇔ cos(a→, b→) = -1 nên a→, b→ ngược hướng.

Đáp án: C

Câu 35:

Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Tích vô hướng $\vec{BA} . \vec{BC}$ bằng:

A. $a^{2}$

B. $- a^{2}$

C. $\frac{a^{2}}{2}$

D. $a^{2} \sqrt{3}$

Xem đáp án

BA→ . BC→ = -AB→(AC→ - AB→) = (-AB→. AC→ ) + AB→² = 0 + a² = a².

Đáp án: A

Câu 36:

Trong mặt phẳng Oxy cho tam giác ABC với A(1; 1), B(2; 4), C(10; -2). Giá trị cosC bằng:

A. $\frac{1}{\sqrt{10}}$

B. $\frac{- 1}{\sqrt{10}}$

C. $\frac{3}{\sqrt{10}}$

D. $\frac{- 3}{\sqrt{10}}$

Xem đáp án

Đáp án: C

Câu 37:

Tam giác ABC có AB = 2cm, AC = 1 cm, góc A = 60^ο. Độ dài cạnh là BC là:

A. 1 cm

B. 2 cm

C. √3 cm

D. √5

Xem đáp án

Áp dụng công thức a² = b² + c² – 2bc.cosA ta tính được a = √3 (cm)

Đáp án: C

Câu 38:

Tam giác ABC có các cạnh a = 5cm, b = 3cm, c = 5cm. Số đo của góc BAC là:

A. A = $45^{o}$

B. A = $30^{o}$

C. A > $60^{o}$

D. A = $90^{o}$

Xem đáp án

Áp dụng công thức cosA = (b² + c²-a²)/2bc ta tính được cosA = 3/10 = 0,3.Vậy A ̂ > 60^o.

Đáp án: C

Câu 39:

Tam giác ABC có AB = 8cm, BC = 10cm, CA = 6cm. Đường trung tuyến AM của tam giác có độ dài bằng:

A. 4cm

B. 5cm

C. 6cm

D. 7cm

Xem đáp án

Đáp án: B

Câu 40:

Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng:

A. 1cm

B. √2

C. 2cm

D. 3cm

Xem đáp án

Dùng công thức S = pr ta có r = S/p = 2 (cm).

Đáp án: C

Câu 41:

Tam giác ABc có các cạnh a = √3cm, b = √2cm, c = 1cm. Đường trung tuyến m_a có độ dài là:

A. 1cm

B. 1,5cm

C. √3/2cm

D. 2,5cm

Xem đáp án

Đáp án: C

Câu 42:

Tam giác đều nội tiếp đường tròn bán kính R = 4cm có diện tích là:

A. 13 ${cm}^{2}$

B. 13√2 ${cm}^{2}$

C. 12√3 ${cm}^{2}$

D. 15 ${cm}^{2}$

Xem đáp án

Ta có S_ABC = 1/2CH. AB với CH = 3/2R và AB = R√3, mà R = 4 nên S_ABC = 12√3 (cm²).

Đáp án: C

Câu 43:

Tam giác ABC vuông và cân tại A có AB = a. Đường tròn nội tiếp tam giác ABC có bán kính r bằng:

A. $\frac{a}{2}$

B. $\frac{a}{\sqrt{2}}$

C. $\frac{a}{2 + \sqrt{2}}$

D. $\frac{a}{3}$

Xem đáp án

Dùng công thức S = pr với

Đáp án: C

Câu 44:

Tam giác ABC có các cạnh a, b, c thỏa mãn điều kiện:

(a + b + c)(a + b - c) = 3ab. Khi đó số đo của góc C là:

A. $120^{o}$

B. $30^{o}$

C. $45^{o}$

D. $60^{o}$

Xem đáp án

(a + b + c)(a + b – c) = 3ab

⇔ (a + b)² - c² = 3ab

⇔ a² + b² + 2ab - c² = 3ab,

Mà a² + b² – 2ab.cosC = c²

Nên 2ab.cosC = ab ⇒ cos C = 1/2 ⇒ ∠C = 60^o.

Đáp án: D

Câu 45:

Hình bình hành ABCD có AB = a, BC = a√2 và góc BAD = 45^οDiện tích hình bình hành bằng:

A. 2 $a^{2}$

B. $a^{2}$ √2

C. $a^{2}$

D. $a^{2}$ √3

Xem đáp án

Cắt hình bình hành theo đường chéo BD rồi ghép cho cạnh BC trùng với AD, ta được một hình vuông cạnh a và S = a².

Đáp án: C

Câu 46:

Tam giác ABC vuông cân tại A có AB = AC = a. Đường trung tuyến BM có độ dài là:

A. 1,5a

B. a√2

C. a√3

D. ( a√5)/2

Xem đáp án

Đáp án: D

Câu 47:

Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Bán kính R bằng:

A. $\frac{a \sqrt{3}}{2}$

B. $\frac{a \sqrt{2}}{3}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{3}}{4}$

Xem đáp án

Tam giác đều cạnh a có đường cao h = (a√3)/2.

Mặt khác h = 3/2R (h.2.37)

Do đó: (a√3)/2 = 3/2R ⇔ a√3 = 3R.

Vậy R = (a√3)/3.

Đáp án: C

Câu 48:

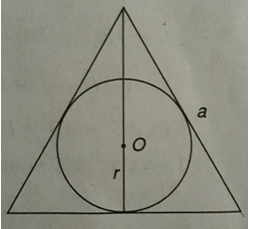
Bán kính của đường tròn nội tiếp tam giác đều cạnh a bằng:

A. $\frac{a \sqrt{3}}{4}$

B. $\frac{a \sqrt{2}}{5}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{5}}{7}$

Xem đáp án

Gọi r là bán kính đường tròn nội tiếp tam giác đều cạnh a (h.2.38). Ta có:

Đáp án: C

Câu 49:

Cho tam giác ABC có cạnh BC = a, cạnh CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. $60^{o}$

B. $90^{o}$

C. $150^{o}$

D. $120^{o}$

Xem đáp án

Ta có S = 1/2ab.sinC,

S đạt cực đại khi sinC = 1 nghĩa là ∠C = 90^o.

Đáp án: B

Câu 50:

Cho tam giác ABC có diện tích S. Nếu tăng độ dài mỗi cạnh BC và AC lên hai lần đồng thời giữ nguyên độ lớn của góc C thì diện tích của tam giác mới được tạo nên là:

A. 2S

B. 3S

C. 4S

D. 5S

Xem đáp án

Gọi S’ là diện tích của tam giác mới, ta có:

S’ = 1/2.2a.2b.sinC = 2ab.sinC.

Vậy S’ = 4S

Đáp án: C

Câu 51:

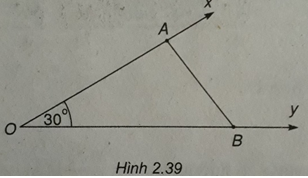
Cho góc xOy = 30^ο. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 2. Độ dài lớn nhất của đoạn OB bằng:

A. 2

B. 3

C. 4

D. 5

Xem đáp án

OB đạt cực đại khi sin A = 1 nghĩa là ∠A = 90^o, khi đó OB = 4.

Đáp án: C

Câu 52:

Cho hai điểm A(0; 1) và B(3; 0). Khoảng cách giữa hai điểm A và B là:

A. 3

B. 4

C. √5

D. √10

Xem đáp án

Ta có AB→ = (3;1). Do đó |AB→| = √(3²+ 1² ) = √10.

Đáp án: D

Câu 53:

Trong mặt phẳng Oxy cho ba điểm A(-1; 1), B(2; 4), C(6; 0). Khẳng định nào sau đây đúng?

A. Tam giác ABC có ba góc nhọn

B. Tam giác ABC có một góc vuông.

C. Tam giác ABC có một góc tù.

D. Tam giác ABC đều.

Xem đáp án

Ta có AB→ = (3; 3), BC→ = (4; -4)

AB→. BC→ = 0. Vậy tam giác ABC vuông tại B.

Hay ta có |AB→| = √(9+9) = √18

|BC→| = √(16+16)= √32.

AC→ = √(49+1)= √50.

Vậy AC²= AB² + BC².

Tam giác ABC vuông tại B có cạnh huyền là AC.

Đáp án: B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Hình học - Chương 2: Tích vô hướng của hai vectơ và ứng dụng

Ôn tập chương 2 - SBT Hình học 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương