Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật có một đỉnh là O, diện tích bằng 12 và đường tròn ngoại tiếp (T) của có có phương trình là . Tìm tọa độ các đỉnh còn lại của hình chữ nhật.
 Giải bởi Vietjack
Giải bởi Vietjack
(Xem hình 3.39)
Đường tròn (T) có tâm T(5/2; 0) và bán kính R = 5/2.
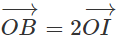
Vậy ta được:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC biết các cạnh a = 13; b = 14; c = 15. Góc B bằng:
Trong mặt phẳng tọa độ Oxy, cho elip (E): . Gọi hai tiêu điểm của (E) lần lượt là F1, F2 và M thuộc (E) sao cho . Tìm tọa độ điểm M và tính diện tích tam giác MF1F2
Cho tam giác ABC có tọa độ các đỉnh là A(1;2), B(3;1), C(5;4). Phương trình đường cao vẽ từ A là:
Cho hai điểm A(3;-1), B(-1;-2) và đường thẳng d có phương trình x + 2y + 1 = 0
a) Tìm tọa độ điểm C trên đường thẳng d sao cho tam giác ABC là tam giác cân tại C.
b) Tìm tọa độ điểm M trên đường thẳng d sao cho tam giác AMB vuông tại M.
Cho tam giác ABC, biết cạnh a = 17,4; góc B = 44ο33'; góc C = 64ο. Cạnh b bằng bao nhiêu?
Trong mặt phẳng Oxy cho các điểm A(1;1), B(2;4), C(10;-2). Tích vô hướng bằng:
Cho ba điểm A(3;5), B(2;3), C(6;2). Đường tròn ngoại tiếp tam giác ABC có phương trình là:
Độ dài trung tuyến mc ứng với cạnh c của tam giác ABC bằng biểu thức nào sau đây?
Cho tam giác ABC với A(-1;1), B(4;7), C(3;-2). Phương trình tham số của trung tuyến CM là:
Cho tam giác ABC có ba cạnh thỏa mãn hệ thức: b + c = 2a. Trong các mệnh đề sau, mện đề nào đúng?
Cho đường tròn (C): x2 + y2 - 4x - 2y = 0 và đường thẳng Δ: x + 2y + 1 = 0
Trong các khẳng định sau, tìm khẳng định đúng.
Trong mặt phẳng Oxy, cho hai điểm A(0;3), B(3;1). Tọa độ điểm M thỏa mãn là:
Cho ba điểm A(1;2), B(-3;1), C(4;-2).
a) Chứng minh rằng tập hợp các điểm M(x;y) thỏa mãn MA2 + MB2 = MC2 là một đường tròn.
b) Tìm tọa độ tâm và bán kính của đường tròn nói trên.
Gọi S là diện tích ta, giác ABC. Trong các khẳng định sau, tìm khẳng định đúng.
Trong mặt phẳng Oxy cho tam giác ABC, biết đỉnh A(1 ; 1) và tọa độ trọng tâm G(1 ; 2). Cạnh AC và đường trung trực của nó lần lượt có phương trình là x + y - 2 = 0 và - x + y - 2 = 0. Các điểm M và N lần lượt là trung điểm của BC và AC.
a) Hãy tìm tọa độ các điểm M và N.
b) Viết phương trình hai đường thẳng chứa hai cạnh AB và BC.