Trong mặt phẳng Oxy cho đường thẳng d: 2x – y + 6 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm I(−2;1).
 Giải bởi Vietjack
Giải bởi Vietjack
Dùng công thức tọa độ của phép đối xứng tâm I(−2;1), ta có: M′ = D1(M)
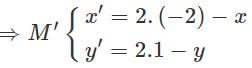
Thế (x;y) vào phương trình d, ta có phương trình:
d′: 2(−4 − x′) − (2 − y′) + 6 = 0
⇒ d′: 2x′ − y′ + 4 = 0.
Đổi kí hiệu, ta có phương trình: d′: 2x – y + 4 = 0
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng Oxy cho đường tròn (C): . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay với O là gốc tọa độ.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình . Viết phương trình đường thẳng là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(−1;2) và phép quay tâm O góc quay .
Trong mặt phẳng Oxy cho đường tròn (C): . Tìm phép tịnh tiến biến (C) thành
(C′): .
Trong mặt phẳng Oxy cho hai đường thẳng d: và d′: . Tìm phép đối xứng qua trục biến d thành d’.
Trong mặt phẳng Oxy cho đường tròn (C): . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d: x = 1.