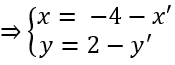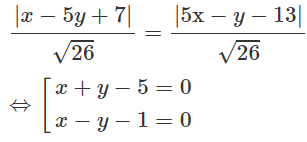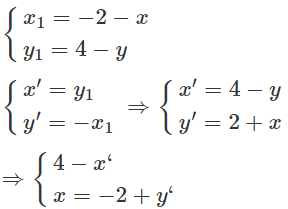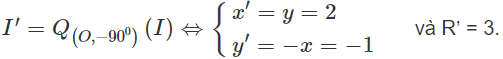6 câu hỏi trắc nghiệm thuộc Đề toán tổng hợp chương 1

Câu 1:

Trong mặt phẳng Oxy cho đường thẳng d: 2x – y + 6 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm I(−2;1).

Xem đáp án

Dùng công thức tọa độ của phép đối xứng tâm I(−2;1), ta có: M′ = D1(M)

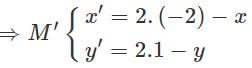
Thế (x;y) vào phương trình d, ta có phương trình:

d′: 2(−4 − x′) − (2 − y′) + 6 = 0

⇒ d′: 2x′ − y′ + 4 = 0.

Đổi kí hiệu, ta có phương trình: d′: 2x – y + 4 = 0

Câu 2:

Trong mặt phẳng Oxy cho đường tròn (C): $x^{2} + y^{2} + 2 x - 4 y - 11 = 0$ . Tìm phép tịnh tiến biến (C) thành

(C′): ${(x - 10)}^{2} + {(y + 5)}^{2} = 16$ .

Xem đáp án

(C) có tâm I(−1;2), bán kính R = 4. (C’) có tâm I′(10; −5), bán kính R’ = 4. Vậy (C′) = $T_{\vec{v}} (C)$ , $\vec{v}$ = II'→ = (11; −7).

Câu 3:

Trong mặt phẳng Oxy cho hai đường thẳng d: $x - 5 y + 7 = 0$ và d′: $5 x - y - 13 = 0$ . Tìm phép đối xứng qua trục biến d thành d’.

Xem đáp án

Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:

Câu 4:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình $3 x - y - 3 = 0$ . Viết phương trình đường thẳng $d_{1}$ là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm I(−1;2) và phép quay tâm O góc quay $- 90 °$ .

Xem đáp án

Giả sử $M_{1} = D_{1} (M)$ và $M' = Q_{(O; - 90 °)} (M_{1})$ . Ta có

Thế (x;y) theo (x′;y′) vào phương trình d ta có:

3(y′ − 2) − (4 − x′) – 3 = 0 ⇔ x′ + 3y′ − 13 = 0

Vậy phương trình d’ là x + 3y – 13 = 0.

Câu 5:

Trong mặt phẳng Oxy cho đường tròn (C): ${(x - 1)}^{2} + {(y - 2)}^{2} = 9$ . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép đối xứng trục d: x = 1.

Xem đáp án

Chỉ cần tìm ảnh của tâm đường tròn qua trục d.

Câu 6:

Trong mặt phẳng Oxy cho đường tròn (C): ${(x - 1)}^{2} + {(y - 2)}^{2} = 9$ . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay $Q_{(0; - 90 °)}$ với O là gốc tọa độ.

Xem đáp án

(C) có tâm I(1;2), bán kính R = 3. Gọi I’; R lần lượt là tâm và bán kính của đường tròn ảnh, ta có:

Vậy phương trình (C’) là ${(x - 2)}^{2} + {(y + 1)}^{2} = 9$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

Đề toán tổng hợp chương 1

Danh sách câu hỏi

Bài thi liên quan