Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Chứng minh \[AK\parallel DF\]
Giải bởi Vietjack
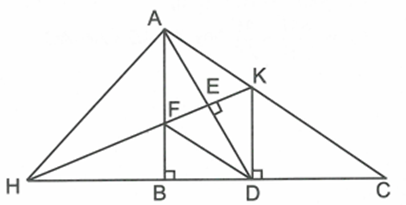
\[\Delta AFK\] có AE vừa là đường cao, vừa là đường phân giác nên cân tại A và E là trung điểm của FK (1)
\[ \Rightarrow \widehat {AFK} = \widehat {AKF}\]. Mà \[\widehat {AFK} = \widehat {DKF}\,\,(AB\parallel DK)\] nên suy ra \[\widehat {AKF} = \widehat {DKF}\]
\[ \Rightarrow \Delta AKD\] cân tại K và E là trung điểm của AD (2)
Từ (1) và (2), suy ra tứ giác AKDF có hai đường chéo AD và FK cắt nhau tại trung điểm của mỗi đường nên AKDF là hình bình hành.
Do vậy \[AK\parallel DF\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\] và \[\Delta CDM\] cânCho tam giác ABC vuông tại A. Kẻ đường cao AH của tam giác.
Kẻ \(HM \bot AB\) và \(HN \bot AC\). Chứng minh \(AM.AB = AN.AC\)
Cho tam giác ABC có \[AB = 18cm,\,AC = 24cm,\,BC = 30cm\]. Gọi M là trung điểm của BC. Qua M kẻ đường vuông góc với BC cắt AB, AC lần lượt ở D, E.
Chứng minh rằng: \[\Delta ABC\sim\Delta MDC\]
Cho tam giác ABC vuông tại B. Đường phân giác AD. Biết \[AB = 6cm,\,\,AC = 10cm\].
Tính BD và CD
Cho tứ giác ABCD có diện tích 36 cm2, trong đó diện tích \[\Delta ABC\] là 11 cm2. Qua điểm B kẻ đường thẳng song song với AC cắt AD ở M, cắt CD ở N. Tính diện tích \[\Delta MND\].
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[A{D^2} = AB.AC - BD.CD\]
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta FHE\sim\Delta BHC\]
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[AE.AC = AF.AB\]
Cho tam giác ABC, AD là tia phân giác của góc A; \[AB < AC\]. Trên tia đối của tia DA lấy điểm I sao cho \[\widehat {ACI} = \widehat {BDA}\]. Chứng minh rằng
\[\Delta ADB\~\Delta ACI;\,\,\Delta ADB\sim\Delta CDI\]
Cho hình thang ABCD \[(AB\parallel CD)\] có \[\widehat {DAB} = \widehat {DBC}\] và \[AD = 5cm,\,AB = 3cm,\,BC = 9cm\].
Chứng minh \[\Delta DAB\sim\Delta CBD\].
Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
Chứng minh rằng \[\Delta AFE\sim\Delta ACB\]
Cho tam giác ABC cân tại A, M là trung điểm của BC. Lấy các điểm D và E trên AB, AC sao cho \[\widehat {DME} = \widehat B\]
Chứng minh rằng \[\Delta MDE\sim\Delta DBM\]
Cho hình bình hành ABCD, trên tia đối của tia DA lấy điểm M sao cho \[DM = AB\], trên tia đối của tia BA lấy điểm N sao cho \[BN = AD\]. Chứng minh:
\[\Delta CBN\sim\Delta MDC\]
Cho tam giác ABC vuông ở A, điểm M thuộc cạnh AC. Kẻ MD vuông góc với BC tại D. Gọi E là giao điểm của AB và MD.
Chứng minh rằng \[MA.MC = MD.ME\]
Cho tam giác ABC vuông tại A có \[AB = 20cm,\,\,BC = 25cm\]. Gọi M là điểm thuộc cạnh AB.
Tính AC
