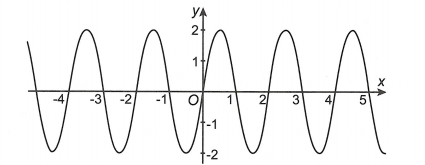
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm tất cả giá trị của tham số m để các bất phương trình đúng với mọi .