b) Hypebol có tiêu cự 2c = 20 và độ dài trục thực 2a = 12;
 Giải bởi Vietjack
Giải bởi Vietjack
b) Gọi phương trình chính tắc của hypebol (H) là
Ta có: 2c = 20 ⇒ c = 10
2a = 12 ⇒ a = 6
Ta lại có: b2 = c2 − a2 = 102 – 62 = 64 ⇒ b = 8.
Thay a = 6 và b = 8 vào phương trình , ta được:
Vậy phương trình chính tắc của hypebol (H) là:
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình là (Hình 17). Biết chiều cao của tháp là 150m và khoảng cách từ nóc tháp đến tấm đối xứng của hypebol bằng khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Cho hypebol (H) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Điểm M thuộc hypebol (H) khi và chỉ khi |F1M – F2M| = 2a. Chọn hệ trục tóa độ Oxy sao cho F1 = (−c; 0) và F2 = (c; 0). Xét điểm M(x; y).
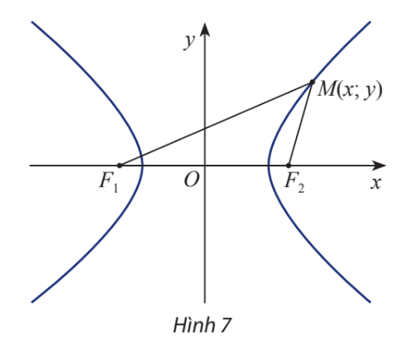
a) Tính F1M và F2M theo x, y và c.
b) Tính khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m đến nóc nhà vòm.
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (Hình 16).
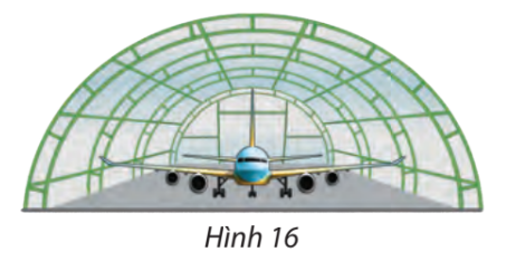
a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên.
Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 20 và trục nhỏ bằng 16;
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục ảo bằng 6.
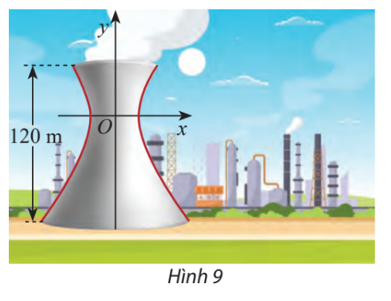
Một tháp làm nguội của một nhà máy có mặt cắt là một hypebol có phương trình (Hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc thấp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tính bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
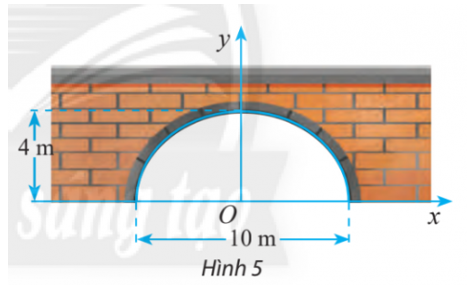
Một đường hầm có mặt cắt hình nửa elip cao 4m, rộng 10m (Hình 5). Viết phương trình chính tắc của elip đó.
Viết phương trình chính tắc của parabol (P) có đường chuẩn Δ: x + 1 = 0
Cho elip (E) có các tiêu điểm F1 và F2 và đặt F1F2 = 2c. Chọn hệ trục tọa độ Oxy sao cho F1(−c; 0) và F2(c; 0). Xét điểm M(x; y).
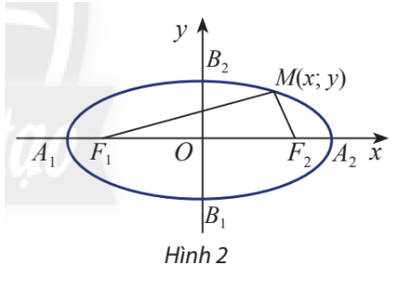
a) Tính F1M và F2M theo x, y và c.
Để cắt một bảng quảng cáo hình elip có trục lớn là 80 cm và trục nhỏ là 40 cm từ một tấm ván ép hình chữ nhật có kích thước 80 cm x 40 cm, người ta vẽ hình elip đó lên tấm ván ép như hướng dẫn sau:
Chuẩn bị:
− Hai cái đinh, một vòng dây kín không đàn hồi, bút chì.
Thực hiện:
− Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tấm ván).
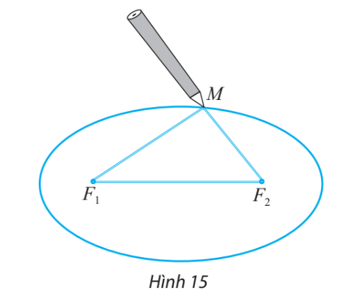
− Quàng vòng dây qua hai chiếc đinh vào kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường elip (Xem minh họa trong Hình 15).
Phải ghim hai cái đinh cách mép tấm ván ép bao nhiêu xentimet và lấy vòng dây có độ dài là bao nhiêu?
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm F1 và F2. Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn F1F2. Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.
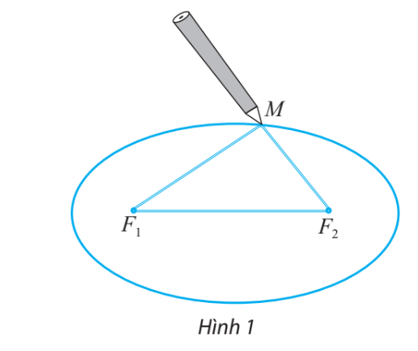
Cho biết 2c là khoảng cách F1F2 và 2a + 2c là độ dài của vòng dây. Tính tổng hai khoảng cách F1M và F2M.
Lấy một tấm bìa, trên đó đánh dấu hai điểm F1 và F2. Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho d − l = 2a nhỏ hơn khoảng cách F1F2 (Hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm F2. Đặt thước sao cho đầu B của thước trùng với điểm F1 và đoạn thẳng BA có thể quay quanh F1. Tựa đầu bút chì M vào đoạn dây, di chuyển M trên tấm bìa và giữ một đường (H) (xem Hình 6b).
a) Chứng tỏ rằng khi M di động, ta luôn có MF1 – MF2 = 2a.