Bài 12: Vẽ hình phẳng bằng GEOGEBRA
-
1479 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
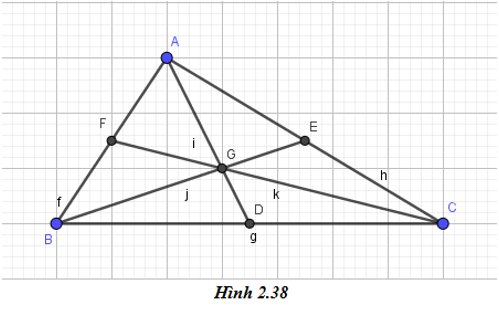
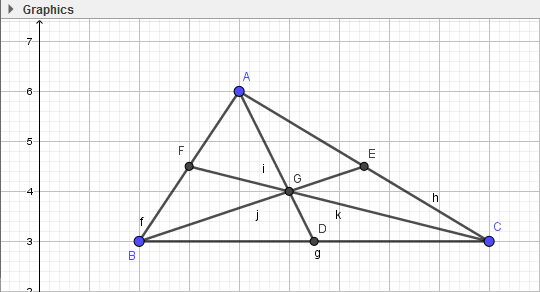
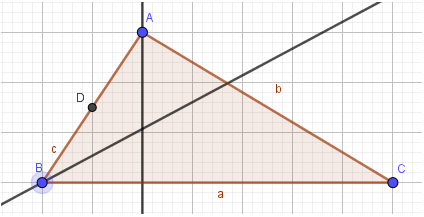
Vẽ tam giác ABC với trọng tâm G và ba đường trung tuyến (hình 2.38).
 Xem đáp án
Xem đáp án
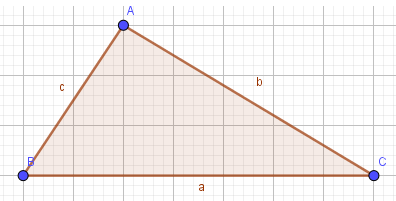
1. Vẽ tam giác ABC:
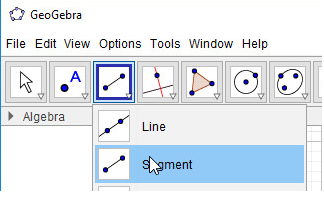
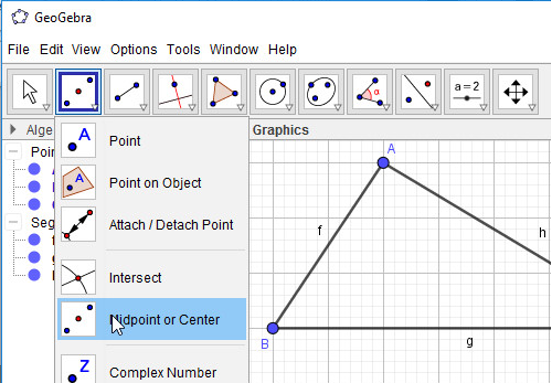
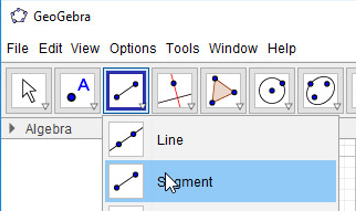
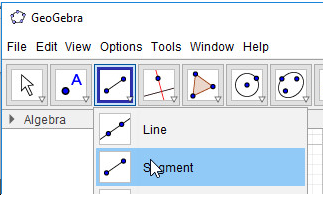
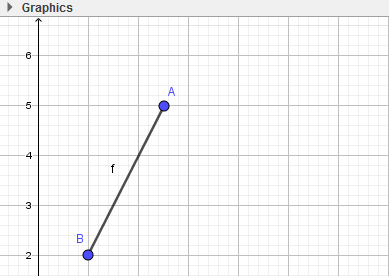
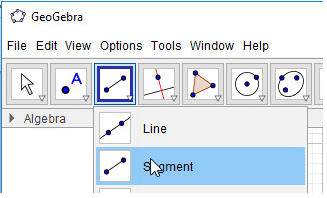
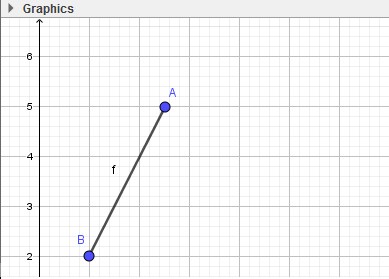
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng
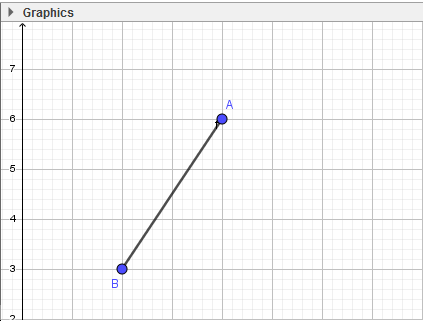
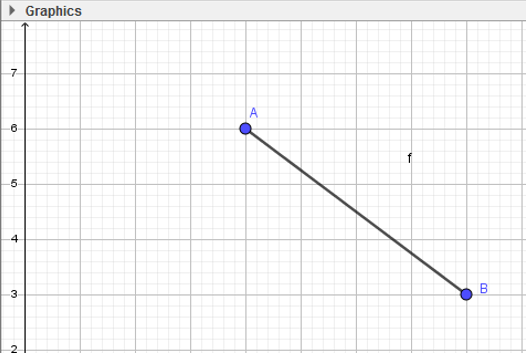
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
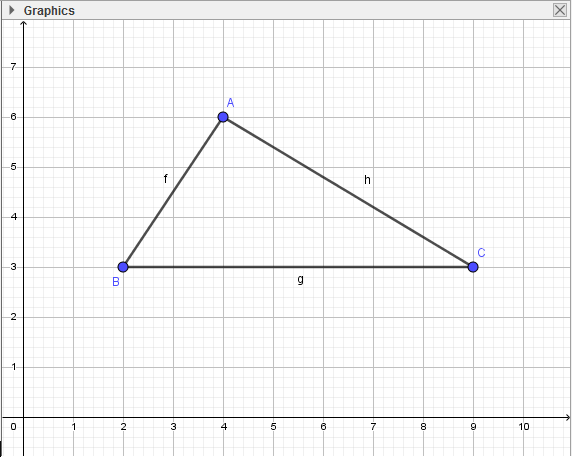
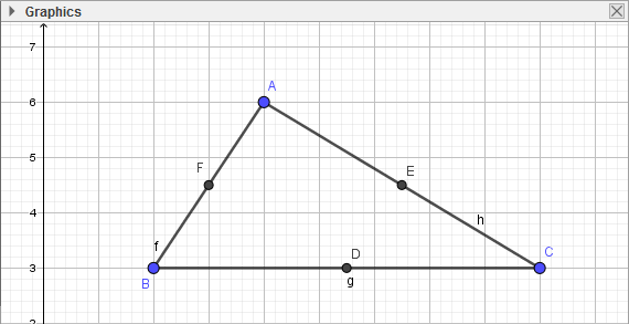
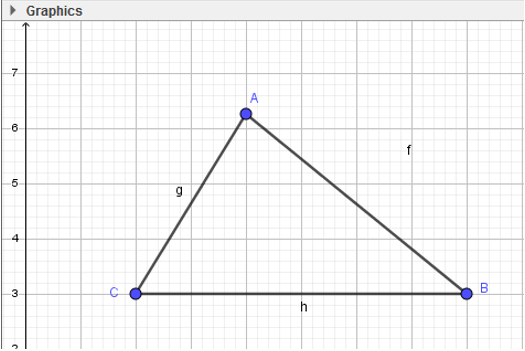
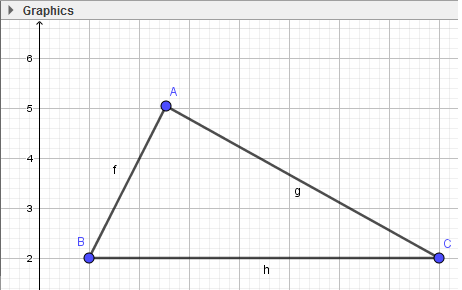
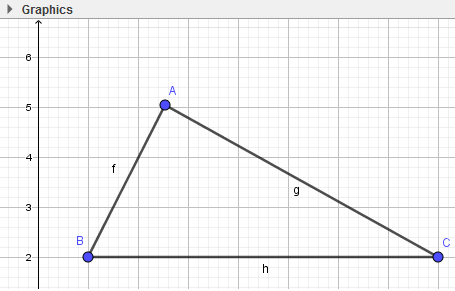
- Bước 3: Thực hiện tương tự, em sẽ tạo được tam giác ABC:
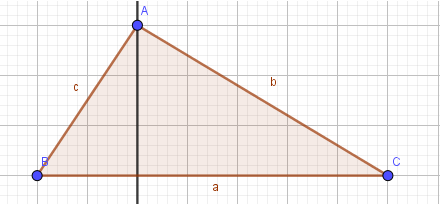
2. Tạo các trung điểm của các cạnh:
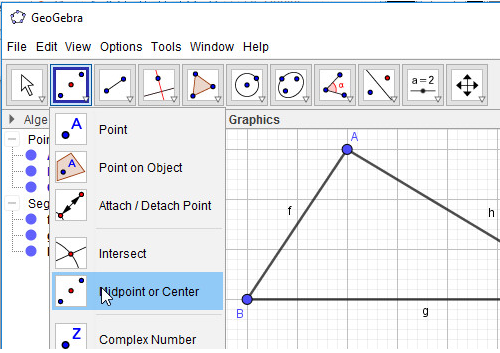
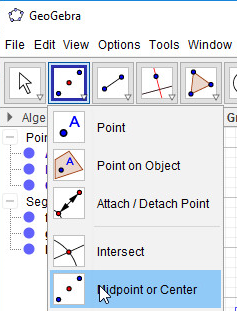
- Bước 1: Chọn công cụ Trung điểm hoặc tâm
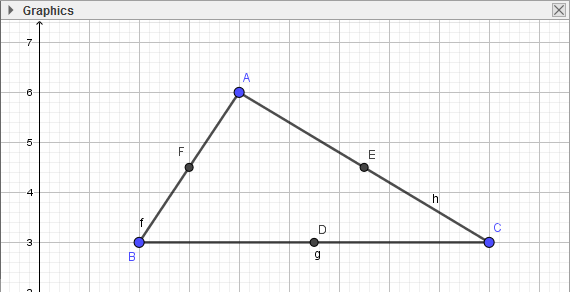
- Bước 2: Lần lượt chọn đối tượng là đoạn thẳng BC, AC, AB:
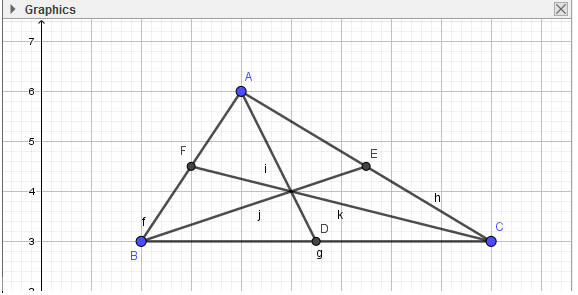
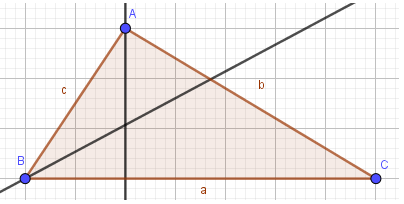
3. Nối các đường trung tuyến
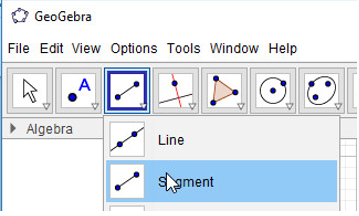
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng
- Bước 2: Lần lượt nháy chuột để xác định điểm đầu và điểm cuối để vẽ đoạn thẳng:
4. Vẽ trọng tâm G:
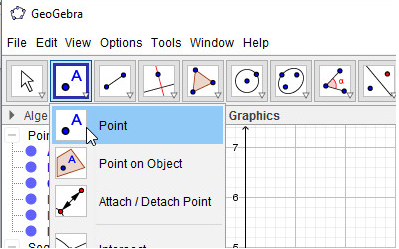
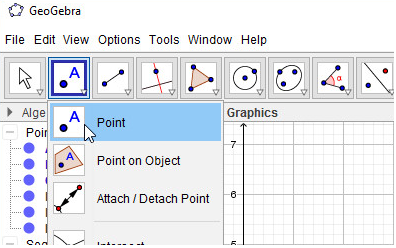
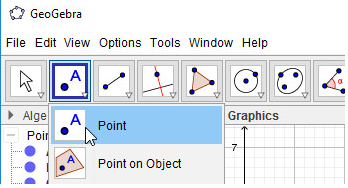
- Bước 1: Nháy chuột chọn công cụ Điểm 
- Bước 2: Nháy chuột vào giao điểm của 3 đường trung tuyến, em được trọng tâm G. Như vậy em đã vẽ được tam giác ABC với trọng tâm G và 3 đường trung tuyến:
Câu 2:
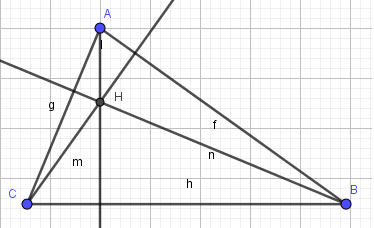
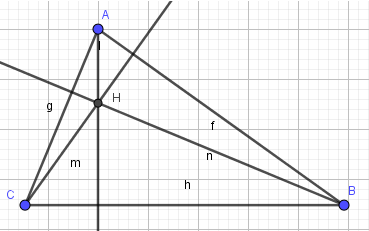
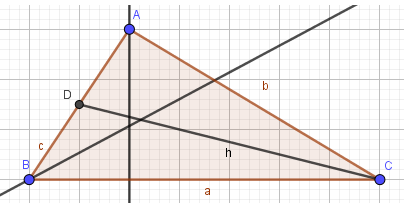
Vẽ tam giác ABC với ba đường cao và trực tâm H
 Xem đáp án
Xem đáp án
1. Vẽ tam giác ABC:
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng 
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
- Bước 3: Thực hiện tương tự, em sẽ tạo được tam giác ABC:
2. Vẽ ba đường cao:
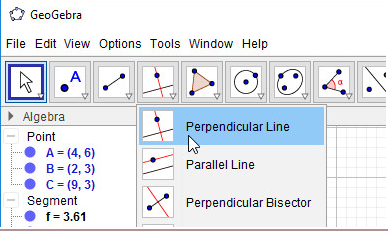
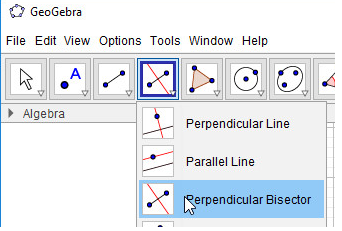
- Bước 1: Chọn công cụ Đường vuông góc
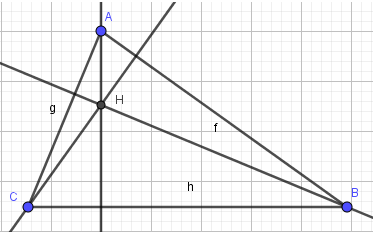
- Bước 2: Chọn điểm A, sau đó chọn đoạn thẳng BC để dựng đường cao qua A. Thực hiện tương tự, em sẽ được 3 đường cao:
3. Vẽ trực tâm H:
- Bước 1: Nháy chuột chọn công cụ Điểm
- Bước 2: Nháy chuột vào giao điểm của 3 đường cao, em được trực tâm H:
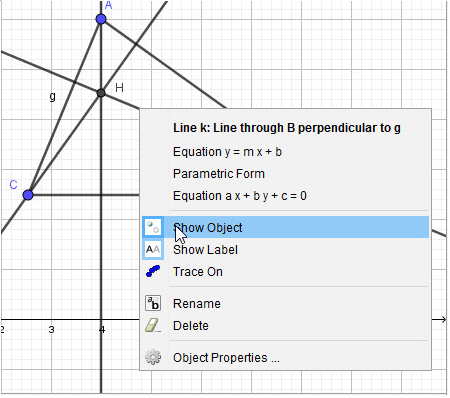
4. Ẩn các đối tượng đường cao:
Lần lượt nhấn chuột phải vào các đường cao và chọn Hiển thị đối tượng (Show Object):
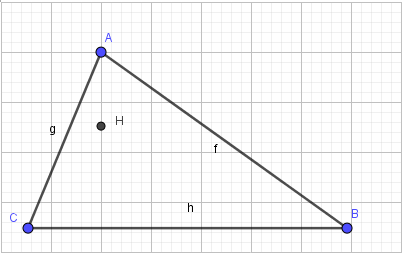
→ Kết quả:
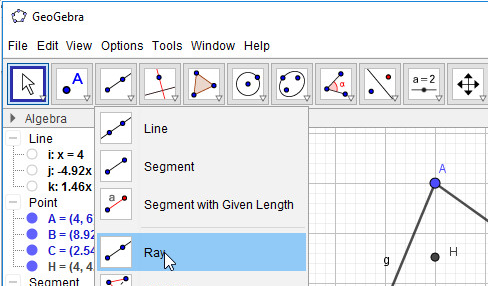
5. Vẽ các tia AH, BH, CH:
- Bước 1: Nháy chuột chọn công cụ Tia 
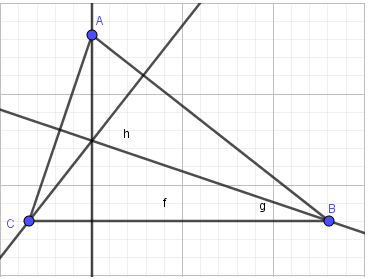
- Bước 2: Lần lượt nháy chuột chọn điểm đầu và điểm đi qua của các tia, em sẽ được tam giác ABC với ba đường cao và trực tâm H như hình 2.39:
Câu 3:
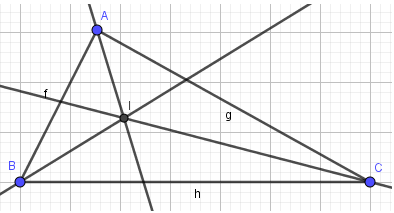
Vẽ tam giác ABC với ba đường phân giác cắt nhau tại điểm I
 Xem đáp án
Xem đáp án
1. Vẽ tam giác ABC:
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng 
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
- Bước 3: Thực hiện tương tự, em sẽ tạo được tam giác ABC:
2. Vẽ ba đường phân giác:
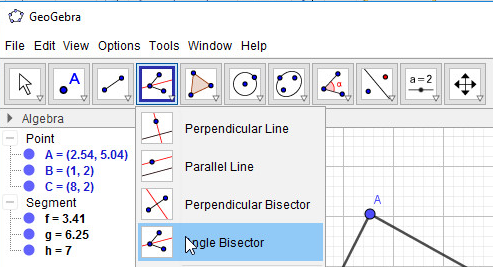
- Bước 1: Chọn công cụ Đường phân giác
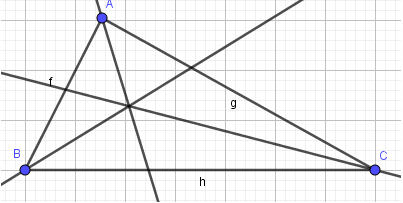
- Bước 2: Lần lượt nháy chọn điểm B, A, C để dựng đường phân giác qua A. Thực hiện tương tự, em sẽ được 3 đường phân giác:
3. Vẽ giao điểm I của ba đường phân giác:
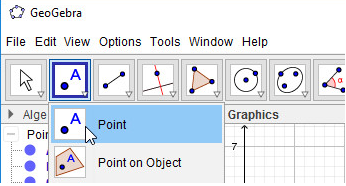
- Bước 1: Nháy chuột chọn công cụ Điểm 
- Bước 2: Nháy chuột vào giao điểm của 3 đường phân giác, em được điểm I. Như vậy em đã vẽ được tam giác ABC với ba đường phân giác cắt nhau tại điểm I:
Câu 4:
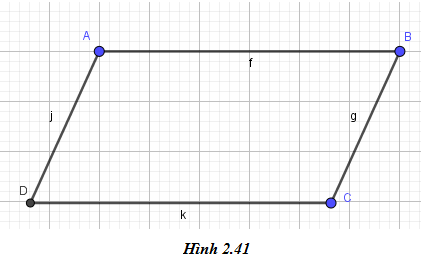
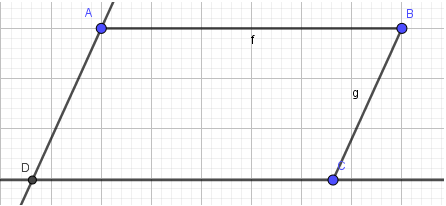
Vẽ hình bình hành ABCD (hình 2.41).
 Xem đáp án
Xem đáp án
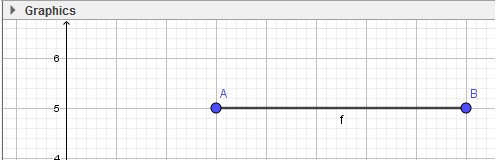
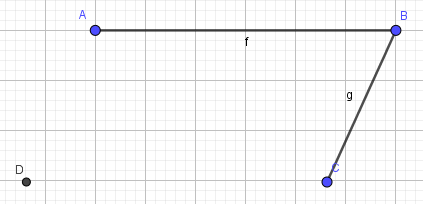
1. Vẽ hai cạnh AB và BC:
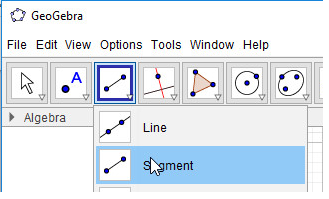
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
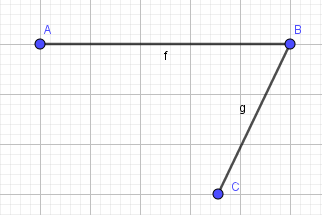
- Bước 3: Tạo cạnh BC bằng cách tương tự như AB:
2. Vẽ điểm D và 2 cạnh còn lại
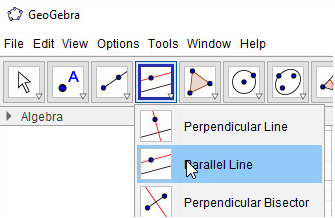
- Bước 1: Nháy chuột chọn công cụ Đường song song
- Bước 2: Chọn điểm, sau đó chọn đoạn thẳng để vẽ đường thẳng song song:
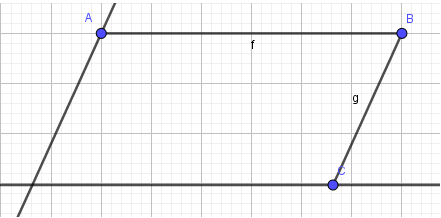
Bước 3: Đánh dấu giao điểm của 2 đường thẳng vừa tạo là điểm D:
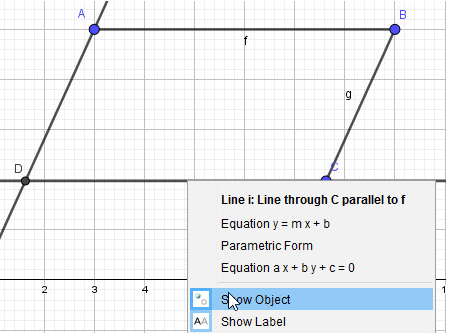
- Bước 4: Ẩn các đối tượng đường song song vừa tạo:
Lần lượt nhấn chuột phải vào các đường thẳng song song vừa tạo và chọn Hiển thị đối tượng (Show Object):
→ Kết quả:
- Bước 5: Sử dụng công cụ Đoạn thẳng
Câu 5:
Vẽ tam giác ABC với ba đường trung trực cắt nhau tại điểm O.
 Xem đáp án
Xem đáp án
1. Vẽ tam giác ABC:
- Bước 1: Nháy chuột chọn công cụ Đoạn thẳng 
- Bước 2: Nháy chuột tại vị trí trống bất kì trên màn hình (em sẽ thấy xuất hiện điểm A), di chuyển đến vị trí thứ hai và nháy chuột. Như vậy ta vừa tạo xong đoạn AB.
- Bước 3: Thực hiện tương tự, em sẽ tạo được tam giác ABC:
2. Tạo các trung điểm của các cạnh:
- Bước 1: Chọn công cụ Trung điểm hoặc tâm
- Bước 2: Lần lượt chọn đối tượng là đoạn thẳng BC, AC, AB:
3. Vẽ ba đường trung trực:
- Bước 1: Chọn công cụ Đường trung trực
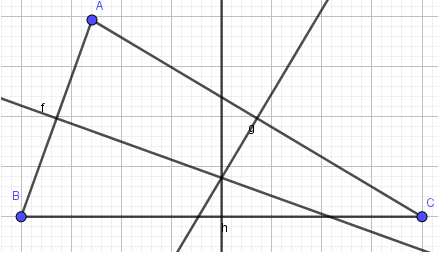
- Bước 2: Lần lượt nháy chọn điểm A, B để dựng đường trung trực của cạnh AB. Thực hiện tương tự, em sẽ được 3 đường trung trực:
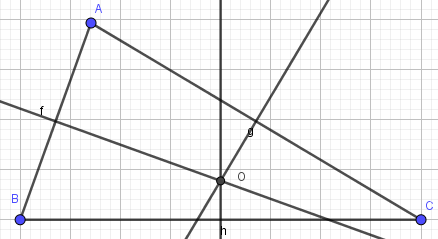
4. Vẽ giao điểm O của ba đường trung trực:
- Bước 1: Nháy chuột chọn công cụ Điểm 
- Bước 2: Nháy chuột vào giao điểm của 3 đường trung trực, em được điểm O. Như vậy em đã vẽ được tam giác ABC với ba đường trung trực cắt nhau tại O:
Câu 6:
Sử dụng công cụĐa giác
 Xem đáp án
Xem đáp án
- Bước 1: Nháy chuột chọn công cụ Đa giác 
- Bước 2: Vẽ đường cao qua A bằng công cụ Đường vuông góc
- Bước 3: Vẽ đường phân giác qua B bằng công cụ Đường phân giác 
- Bước 4: Vẽ đường trung tuyến CM:
Chọn công cụ Trung điểm hoặc tâm
Chọn đối tượng là đoạn thẳng là AB để xác định trung điểm D của đoạn thẳng AB:
Sử dụng công cụ đoạn thẳng nối CD, em sẽ được đường trung tuyến CD:
Câu 7:
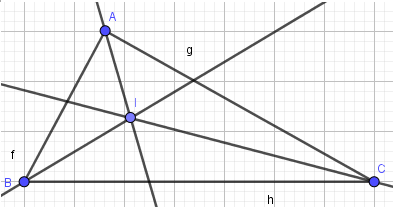
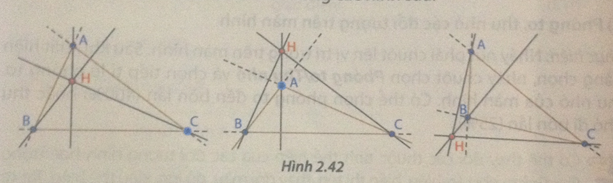
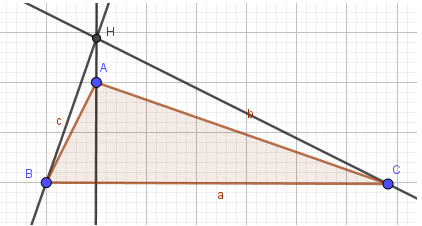
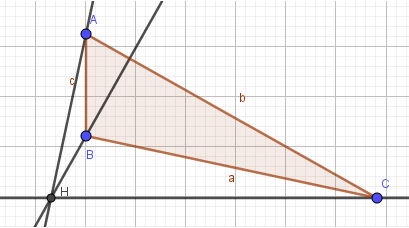
Vẽ tam giác ABC, vẽ các đường cao cắt nhau tại trực tâm H. Em cần thực hiện hình vẽ sao cho khi di chuyển các điểm A, B, C đến các vị trí khác nhau chúng ta lần lượt nhận được các hình như trong các hình sau:
 Xem đáp án
Xem đáp án
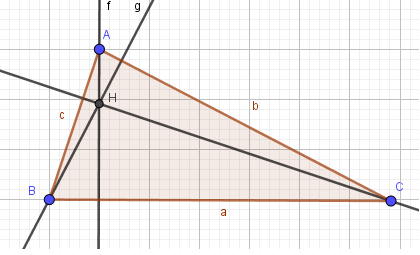
Thực hiện như Câu 2, em sẽ được tam giác ABC với các đường cao cắt nhau tại trực tâm H như sau:
Nháy chuột chọn công cụ Chọn
Đưa con trỏ chuột vào vị trí điểm A, giữ điểm A và kéo thả chuột em sẽ được hình sau:
Đưa con trỏ chuột vào vị trí điểm B, giữ điểm B và kéo thả chuột em sẽ được hình sau:
Câu 8:
Quan sát hình 2.43. Khẳng định sau là đúng hay sai? Tại sao?
A, B là các điểm tự do, đường thẳng d là đối tượng phụ thuộc vào A, B.
 Xem đáp án
Xem đáp án
Khẳng định đúng vì muốn vẽ đường thẳng thẳng bằng GeoGebra phải xác định hai điểm đi qua nên đường thẳng d được tạo qua hai điểm A, B. Nghĩa là, hai điểm A, B là các điểm tự do có thể thay đổi vị trí và đường thẳng d sẽ thay đổi theo để d luôn đi qua hai điểm A, B → d phụ thuộc vào A, B.
Câu 9:
Vì sao các hình được tạo trong GeoGebra được gọi là hình học động?
 Xem đáp án
Xem đáp án
Vì phần mềm GeoGebra không những cho phép tạo các hình vẽ chính xác mà còn có chức năng làm cho các hình này chuyển động khi di chuyển một đối tượng trong hình nên các hình được tạo trong GeoGebra được gọi là hình học động
Câu 10:
Những đặc trưng nào là cơ bản nhất đối với các đối tượng của hình học động?
 Xem đáp án
Xem đáp án
Những đặc trưng cơ bản nhất đối với các đối tượng của hình học động là:
- Các đối tượng hình học có các quan hệ toán học chặt chẽ.
- Nếu quan hệ giữa các đối tượng hình học đã được thiết lập thì sẽ không bao giờ thay đổi.
Câu 11:
Ngược lại với hình học động ta có hình học tĩnh. Để tiếp thu một bài học theo em hình học động tốt hơn hay hình học tĩnh tốt hơn? Vì sao? Hãy phát biểu các ý kiến và quan điểm của cá nhân em.
 Xem đáp án
Xem đáp án
Theo em, để tiếp thu một bài học thì hình học động tốt hơn. Vì ngoài việc các đối tượng hình học động có quan hệ toán học chặt chẽ nên sẽ thể hiện chính xác hình vẽ tĩnh thì hình học động giúp em có cái nhìn trực quan hơn về việc thay đổi của các hình trong các bài toán quỹ tích.
Câu 12:
Có thể phát triển từ khái niệm hình học động tổng quát thành toán học động được không? Em hãy đưa ra lí giải của mình.
 Xem đáp án
Xem đáp án
Theo em có thể phát triển từ khái niệm hình học động tổng quát thành toán học động được. Vì dựa theo khái niệm, hình học động là mô hình hình học gồm các đối tượng hình học và các thiết lập quan hệ giữa chúng, từ đó có thể phát triển lên khái niệm toán học động là mô hình toán học gồm các đối tượng toán học và các thiết lập quan hệ giữa chúng.