Giải bài tập Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Hoạt động khởi động trang 61 Toán lớp 10 Tập 1: Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?

Lời giải:

Để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0^o đến 180^o, ta thực hiện xác định các góc trên nửa đường tròn đơn vị, sau đó sử dụng tỉ số lượng giác của góc nhọn.

1. Giá trị lượng giác

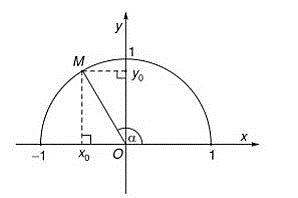
Hoạt động khám phá 1 trang 61 Toán lớp 10 Tập 1: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$. Giả sử điểm M có tọa độ (x₀; y₀). Trong tam giác vuông OHM, áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9 , chứng tỏ rằng:

sinα = y₀; cosα = x₀ ; tanα =  $\frac{y_0}{x_0}$; cotα = $\frac{x_0}{y_0}$

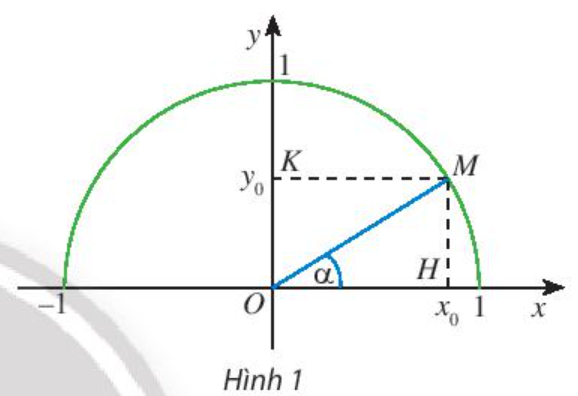
Lời giải:

Ta có : OM = R = 1

Áp dụng hệ thức lượng trong tam giác vuông OHM ta có:

$\sin \alpha =\frac{MH}{MO}=\frac{y_0}{1}=y_0$

$\cos \alpha =\frac{OH}{MO}=\frac{x_0}{1}=x_0$

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{y_0}{x_0}$

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{x_0}{y_0}$

Thực hành 1 trang 62 Toán lớp 10 Tập 1: Tìm các giá trị lượng giác của góc 135°.

Lời giải:

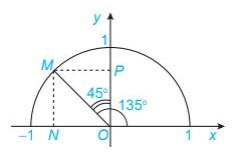
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho $\widehat{xOM}={135}^0$nên $\widehat{yOM}={45}^0$

Gọi N và P tương ứng là hình chiếu vuông góc của M lên các trục Ox và Oy

Xét ∆ MOP vuông cân tại P ta có :

 $\begin{array}{l}O{P}^2+M{P}^2=O{M}^2\\ 2O{P}^2=O{M}^2\\ O{P}^2=\frac{O{M}^2}{2}=\frac{1}{2}\\ \Rightarrow OP=\frac{\sqrt{2}}{2}\end{array}$

Tương tự, xét ∆ NOP vuông cân tại P ta có : ON = $\frac{\sqrt{2}}{2}$

Do N nằm trên khoảng -1 đến 0 nên M ($\frac{-\sqrt{2}}{2}$;$\frac{\sqrt{2}}{2}$)

Vậy $\sin {135}^0=\frac{\sqrt{2}}{2};\cos {135}^0=\frac{-\sqrt{2}}{2}$; tan 135° = -1; cot 135° = -1.

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Hoạt động khám phá 2 trang 62 Toán lớp 10 Tập 1: Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc  $\widehat{xOM}$ và $\widehat{xON}$

Lời giải:

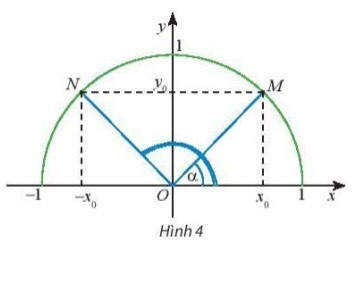
Vì NM // Ox nên $\widehat{xOM}=\widehat{NMO}$.

Xét tam giác OMN cân tại O ta có:

$\widehat{ONM}+\widehat{NMO}+\widehat{NOM}={180}^0$ hay $2\widehat{NMO}+\widehat{NOM}={180}^0\left(1\right)$

Ta có: $\widehat{xOM}$+ $\widehat{xON}$= $\widehat{xOM}+\widehat{xOM}+\widehat{NOM}$

                                = $2.\widehat{NMO}+\widehat{NOM}\left(2\right)$

Từ (1) và (2) ta có: $\widehat{xOM}+\widehat{xON}={180}^0$

Thực hành 2 trang 63 Toán lớp 10 Tập 1: Tính các giá trị lượng giác: sin120°; cos150°; cot135°.

Lời giải:

sin120° = sin(180° – 60°) = sin60° = $\frac{\sqrt{3}}{2}$;

cos150° = cos(180° – 30°) = – cos30° =  $-\frac{\sqrt{3}}{2}$;

cot135° = cot(180° – 45°) = – cot45° = –1.

Vận dụng 1 trang 63 Toán lớp 10 Tập 1: Cho biết $\sin \alpha =\frac{1}{2}$ , tìm góc α (0° ≤ α  ≤ 180°) bằng cách vẽ nửa đường tròn đơn vị.

Lời giải:

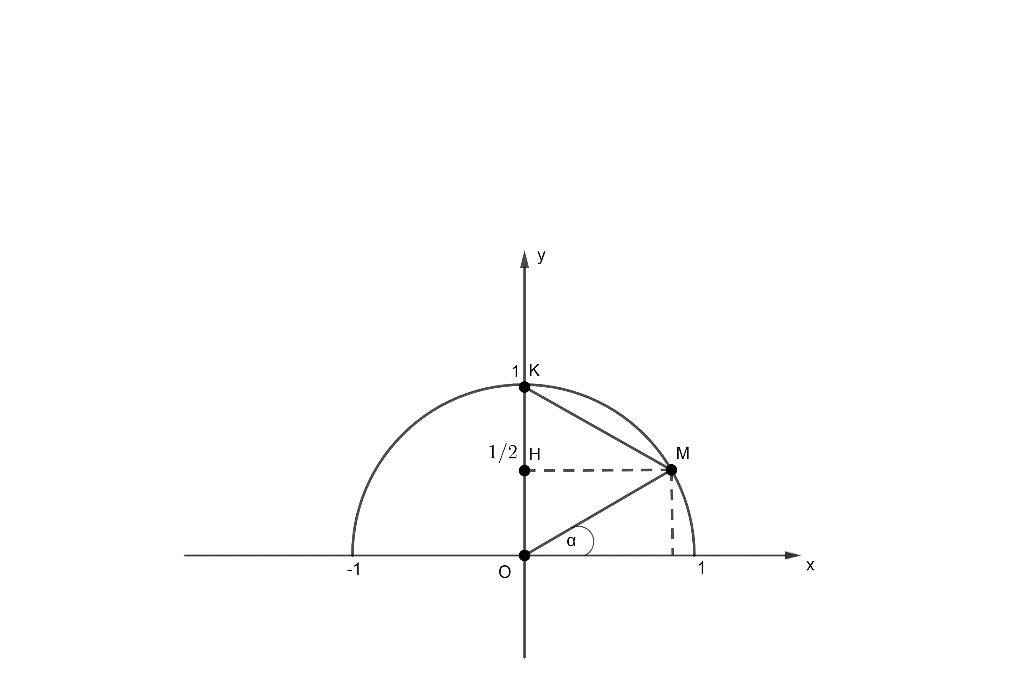
Gọi H($0;\frac{1}{2})$, K (0,1).

Gọi M là một điểm thuộc nửa đường tròn đơn vị sao cho HM//Ox.

Xét ∆MHK vuông tại H ta có: $M{K}^2=H{M}^2+H{K}^2$

Mà OH = HK (vì OH = $\frac{1}{2}$OK)

$\Rightarrow M{K}^2=H{M}^2+H{K}^2=H{M}^2+O{H}^2=O{M}^2$

$\Rightarrow OM=HK=OK$hay tam giác OMK là tam giác đều

$\begin{array}{l}\Rightarrow \widehat{KOM}={60}^0\\ \Rightarrow \widehat{MOx}={90}^0-{60}^0={30}^0\end{array}$

hay $\alpha ={30}^0$.

3. Giá trị lượng giác của một số góc đặc biệt

Thực hành 3 trang 63 Toán lớp 10 Tập 1: Tính

A = sin150° + tan135°  + cot45°;

B = 2cos30° – 3tan150° + cot135°.

Lời giải:

$A=\sin {150}^0+\tan {135}^0+\cot {45}^0$

$=\frac{1}{2}+(-1)+1=\frac{1}{2}$

$B=2\cos {30}^0-3\tan {150}^0+\cot {135}^0$

$=2.\frac{\sqrt{3}}{2}-3.\left(\frac{-\sqrt{3}}{3}\right)+(-1)$

$=2\sqrt{3}-1$

Vận dụng 2 trang 64 Toán lớp 10 Tập 1: Tìm góc α  (0° ≤ α  ≤ 180°) trong mỗi trường hợp sau:

a) sinα  = $\frac{\sqrt{3}}{2}$;

b) cosα = $\frac{-\sqrt{2}}{2}$ ;

c) tanα  =  – 1;

d) cotα  =  $-\sqrt{3}$.

Lời giải:

Áp dụng bảng giá trị lượng giác của các góc đặc biệt, ta được:

a) $\sin \alpha =\frac{\sqrt{3}}{2}$ khi α = 60^o hoặc α = 120^o.

b) $\cos \alpha =-\frac{\sqrt{2}}{2}$ khi α = 135^o.

c) tan α = -1 khi α = 135^o.                  

d) cot α = $-\sqrt{3}$khi α = 150^o.

4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc

Thực hành 4 trang 65 Toán lớp 10 Tập 1:

a) Tính cos80°43'51"; tan147°12'25''; cot99°9'19".

b) Tìm α (0° ≤ α  ≤ 180°), biết cosα  = – 0,723.

Lời giải:

a) Sử dụng máy tính cầm tay, ta có:

$\cos 80°43\text{'}51"$ ≈ 0,161072728;

$\tan 147°12\text{'}25"$ ≈ -0,6442844943;

$\cot 99°9\text{'}19"$ ≈ -0,1611637334.

b) Ta có: cosα = $-$ 0,723 suy ra α ≈ $136°19\text{'}$.

Bài tập

Bài 1 trang 65 Toán lớp 10 Tập 1: Cho biết sin30° = $\frac{1}{2}$; sin60° = $\frac{\sqrt{3}}{2}$ ; tan45° = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30° + sin150° + tan135°.

Lời giải:

$E=2\cos {30}^0+\sin {150}^0+\tan {135}^0$

$=2\cos ({90}^0-{60}^0)+\sin ({180}^0-{30}^0)+\tan ({180}^0-{45}^0)$

$=2\sin {60}^0+\sin {30}^0-\tan {45}^0$

$=2.\frac{\sqrt{3}}{2}+\frac{1}{2}-1=\sqrt{3}-\frac{1}{2}$

Bài 2 trang 65 Toán lớp 10 Tập 1: Chứng minh rằng:

a) sin20° = sin160°;

b) cos50° =  – cos130°.

Lời giải:

a) Ta có: $\sin {20}^0=\sin ({180}^0-{160}^0)=\sin {160}^0$(đpcm)

b) Ta có: $\cos {50}^0=\cos ({180}^0-{130}^0)=-\cos {130}^0$(đpcm)

Bài 3 trang 65 Toán lớp 10 Tập 1: Tìm α (0° ≤ α  ≤ 180°) trong mỗi trường hợp sau:

a) cosα  = $\frac{-\sqrt{2}}{2}$ ;

b) sinα  = 0;

c) tanα  = 1;

d) cotα  không xác định.

Lời giải:

a)$\cos \alpha =\frac{-\sqrt{2}}{2}$ khi α = 135^o. 

b) sin α = 0 khi α = 0^o hoặc α = 180^o.

c) tan α = 1 khi α = 45^o.

d) cot α không xác định khi α = 0^o hoặc α = 180^o.

Bài 4 trang 65 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh rằng:

a) sinA = sin(B + C);

b) cosA =  – cos(B + C).

Lời giải:

Xét ∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}={180}^0$(định lí tổng ba góc trong một tam giác)

nên $\widehat{A}={180}^0-(\widehat{B}+\widehat{C})$ 

a) $\sin A=\sin ({180}^0-(B+C\left)\right)=\sin (B+C)$(đpcm)

b)$\cos A=\cos ({180}^0-(B+C\left)\right)=-\cos (B+C)$ (đpcm)

Bài 5 trang 65 Toán lớp 10 Tập 1: Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có:

a) cos²α  + sin²α  = 1;

b) tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°).

c) 1 + tan²α  = $\frac{1}{{\cos }^2\alpha }$ (α  ≠ 90°);

d) 1 + cot² α  = $\frac{1}{{\sin }^2\alpha }$ (0° < α  < 180°).

Lời giải:

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho $\widehat{xOM}=\alpha$($0^0\le \alpha \le {180}^0$). Khi đó, ta có:

$\sin \alpha =y_0;\cos \alpha =x_0,\tan \alpha =\frac{y_0}{x_0};\cot \alpha =\frac{x_0}{y_0}$

a) ${\cos }^2\alpha +{\sin }^2\alpha ={x_0}^2+{y_0}^2=O{M}^2=1$. Vậy ${\cos }^2\alpha +{\sin }^2\alpha =1$.

b) Với $0^0<\alpha <{180}^0$; α ≠ ${90}^0$:

tanα. cotα = $\frac{y_0}{x_0}.\frac{x_0}{y_0}=1$

Vậy tanα. cotα =1 ($\frac{y_0}{x_0}.\frac{x_0}{y_0}=1$; α ≠ ${90}^0$).

c) $1+{\tan }^2\alpha =1+\frac{{\sin }^2\alpha }{{\cos }^2\alpha }=\frac{{\cos }^2\alpha +{\sin }^2\alpha }{{\cos }^2\alpha }=\frac{1}{{\cos }^2\alpha }$$(\alpha \ne {90}^0)$.

Vậy $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }(\alpha \ne {90}^0)$.       

d)  $1+{\cot }^2\alpha =1+\frac{{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{{\sin }^2\alpha +{\cos }^2\alpha }{{\sin }^2\alpha }=\frac{1}{{\sin }^2\alpha }(0^0<\alpha <{180}^0)$.

Vậy $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }(0^0<\alpha <{180}^0)$.

Bài 6 trang 65 Toán lớp 10 Tập 1: Cho góc α với cosα  = $-\frac{\sqrt{2}}{2}$ . Tính giá trị của biểu thức A = 2sin²α  + 5cos²α .

Lời giải:

$A=2{\sin }^2\alpha +5{\cos }^2\alpha$

$=2{\sin }^2\alpha +2{\cos }^2\alpha +3{\cos }^2\alpha$

$=2({\sin }^2\alpha +{\cos }^2\alpha )+3{\cos }^2\alpha$

$=2+3{\cos }^2\alpha$(vì ${\cos }^2\alpha +{\sin }^2\alpha =1$)

$=2+3{\left(-\frac{\sqrt{2}}{2}\right)}^2$

$=2+\frac{3}{2}=\frac{7}{2}$

Bài 7 trang 65 Toán lớp 10 Tập 1: Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:

a) Tính: sin168°45'33"; cos17°22'35"; tan156°26'39"; cot 56°36'42".

b) Tìm α (0° ≤ α  ≤ 180°) trong các trường hợp sau:

i) sinα  = 0,862;

ii) cosα  =  – 0,567;

iii) tanα  = 0,334.

Lời giải:

a)

 $\sin 168°45\text{'}33"$ ≈ 0,1949334051

$\cos 17°22\text{'}35"$ ≈ 0,9543634797

$\tan 156°26\text{'}39"$ ≈ -0,4359715781

$\cot 56°36\text{'}42"$≈ 0,6590863967

b) Với $0^0\le \alpha \le {180}^0$

i) sinα = 0,862 suy ra $\alpha \approx 59°32\text{'}31"$            

ii) cosα = -0,567 suy ra $\alpha \approx 124°32\text{'}29"$

iii) tanα = 0,334 suy ra $\alpha \approx 18°28\text{'}10\text{'}\text{'}$

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: