Giải bài tập Toán 10 Bài 1: Khái niệm vectơ

1. Định nghĩa vectơ

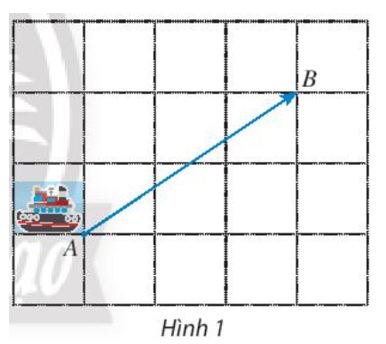
Hoạt động khám phá 1 trang 81 Toán lớp 10 Tập 1: Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.

Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

- Khối lượng của hàng: 500 tấn.

- Độ dịch chuyển của tàu: 500 km từ A đến B.

Lời giải:

Khối lượng của hàng: 500 tấn biểu thị khối lượng hàng mà tàu cần chở là 500 tấn. Đại lượng này vô hướng.

Độ dịch chuyển của tàu: 500 km từ A đến B biểu thị quãng đường tàu cần di chuyển. Đại lượng này có hướng.

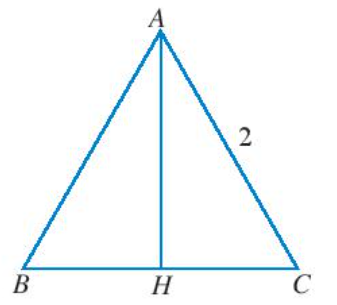
Thực hành 1 trang 82 Toán lớp 10 Tập 1: Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ $\overrightarrow{CH},\overrightarrow{CB},\overrightarrow{HA}$ trong Ví dụ 1. Biết tam giác đều ABC có cạnh bằng 2 và H là trung điểm của đoạn thẳng BC.

Lời giải:

Tam giác ABC đều lại có H là trung điểm của BC nên AH vừa là đường trung tuyến, vừa là đường cao trong tam giác ABC.

Ta có HC = $\frac{1}{2}$BC = 1.

Áp dụng định lí Pythagore vào tam giác AHC vuông tại H ta có:

AH² + HC² = AC²

$\Rightarrow$ AH² = 2² - 1²

$\Rightarrow$ AH² = 3

$\Rightarrow$ AH = $\sqrt{3}$

Vectơ $\overrightarrow{CH}$ có điểm đầu là C, điểm cuối là H, có giá là đường thẳng CH và $\left|\overrightarrow{CH}\right|$ = 1.

Vectơ $\overrightarrow{CB}$ có điểm đầu là C, điểm cuối là B, có giá là đường thẳng CB và $\left|\overrightarrow{CB}\right|$ = 2.

Vectơ $\overrightarrow{HA}$ có điểm đầu là H, điểm cuối là A, có giá là đường thẳng HA và $\left|\overrightarrow{HA}\right|=\sqrt{3}$.

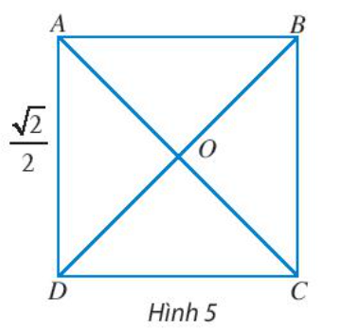
Thực hành 2 trang 82 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng $\frac{\sqrt{2}}{2}$ , hai đường chéo cắt nhau tại O (Hình 5). Tìm độ dài của các vectơ  $\overrightarrow{AC},\overrightarrow{BD},\overrightarrow{OA},\overrightarrow{AO}$.

Lời giải:

Áp dụng định lí Pythagore vào tam giác ABD vuông tại A:

BD² = AB² + AD²

$\Rightarrow$ BD² = ${\left(\frac{\sqrt{2}}{2}\right)}^2+{\left(\frac{\sqrt{2}}{2}\right)}^2$

$\Rightarrow$ BD² = 1

$\Rightarrow$ BD = 1 (do BD là độ dài đoạn thẳng nên BD > 0)

Do ABCD là hình vuông có hai đường chéo cắt nhau tại O nên AC = BD và O là trung điểm của AC.

Do đó AC = BD = 1 và OA = $\frac{1}{2}$AC = $\frac{1}{2}$.

Vậy $\left|\overrightarrow{AC}\right|=\left|\overrightarrow{B\text{D}}\right|$ = 1 và $\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\frac{1}{2}$.

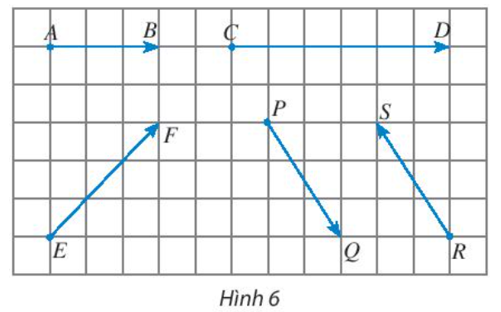
Hoạt động khám phá 2 trang 83 Toán lớp 10 Tập 1: Bạn có nhận xét gì về giá của các cặp vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$,  $\overrightarrow{PQ}$ và $\overrightarrow{RS}$ trong Hình 6?

Lời giải:

Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB; giá của vectơ $\overrightarrow{C\text{D}}$ là đường thẳng CD.

Đường thẳng AB và CD trùng nhau nên giá của hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{C\text{D}}$ trùng nhau.

Giá của vectơ $\overrightarrow{PQ}$ là đường thẳng PQ, giá của vectơ $\overrightarrow{RS}$ là đường thẳng RS.

Đường thẳng PQ và đường thẳng RS song song với nhau nên giá của hai vectơ $\overrightarrow{PQ}$ và $\overrightarrow{RS}$ song song với nhau.

Thực hành 3 trang 84 Toán lớp 10 Tập 1: Quan sát Hình 8 và gọi tên các vectơ:

a) Cùng phương với vectơ $\overrightarrow{x}$;

b) Cùng hướng với vectơ $\overrightarrow{a}$;

c) Ngược hướng với vectơ $\overrightarrow{u}$.

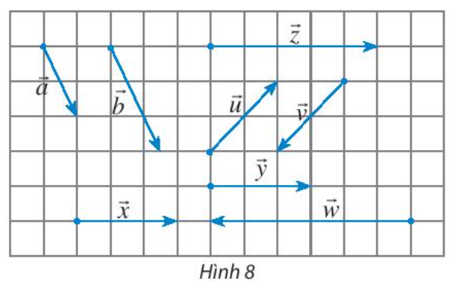
Lời giải:

a) Các vectơ cùng phương với vectơ $\overrightarrow{x}$ là: vectơ $\overrightarrow{y}$, vectơ $\overrightarrow{w}$ và vectơ $\overrightarrow{z}$.

b) Vectơ cùng hướng với vectơ $\overrightarrow{a}$ là: vectơ $\overrightarrow{b}$.

c) Vectơ ngược hướng với vectơ $\overrightarrow{u}$ là: vectơ $\overrightarrow{v}$.

Thực hành 4 trang 84 Toán lớp 10 Tập 1: Khẳng định sau đúng hay sai? Hãy giải thích.

Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

Lời giải:

TH1. A, B, C thẳng hàng; A nằm ngoài đoạn thẳng BC

Ta có A, B, C thẳng hàng; B và C cùng nằm ở một phía so với điểm A (1).

Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB, giá của vectơ $\overrightarrow{AC}$ là đường thẳng AC.

Vì A, B, C thẳng hàng nên đường thẳng AB và đường thẳng AC trùng nhau (2).

Từ (1) và (2) ta có hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

TH2. A, B, C thẳng hàng; A nằm giữa B và C

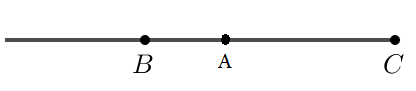
Ta có A, B, C thẳng hàng; B và C cùng nằm khác phía so với điểm A (1).

Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB, giá của vectơ $\overrightarrow{AC}$ là đường thẳng AC.

Vì A, B, C thẳng hàng nên đường thẳng AB và đường thẳng AC trùng nhau (2).

Từ (1) và (2) ta có hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ ngược hướng. 

Hoạt động khám phá 3 trang 84 Toán lớp 10 Tập 1: Cho hình bình hành ABCD (Hình 10), hãy so sánh độ dài và hướng của hai vectơ:

a) $\overrightarrow{AB}$ và $\overrightarrow{DC}$;

b) $\overrightarrow{AD}$ và $\overrightarrow{CB}$.                                                    

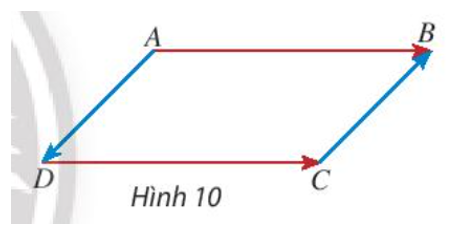
Lời giải:

a) Ta thấy hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

Do ABCD là hình bình hành nên AB = CD.

Do đó $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{C\text{D}}\right|$.

b) Ta thấy hai vectơ $\overrightarrow{A\text{D}}$ và $\overrightarrow{CB}$ ngược hướng.

Do ABCD là hình bình hành nên AD = BC.

Do đó $\left|\overrightarrow{AD}\right|=\left|\overrightarrow{BC}\right|$.

Thực hành 5 trang 85 Toán lớp 10 Tập 1: Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC (Hình 14).

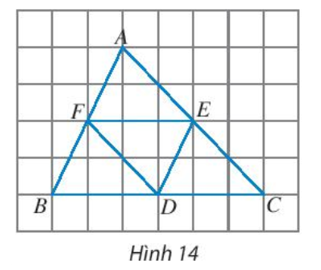
a) Tìm các vectơ bằng vectơ $\overrightarrow{EF}$.

b) Tìm các vectơ đối của vectơ $\overrightarrow{EC}$.

Lời giải:

a) Tam giác ABC có E là trung điểm của AC, F là trung điểm của AB nên EF là đường trung bình của tam giác ABC.

Do đó EF // BC và EF = $\frac{1}{2}$BC.

Do D là trung điểm của BC nên DB = DC = $\frac{1}{2}$BC.

Ta thấy các vectơ $\overrightarrow{DB}$ và $\overrightarrow{CD}$ cùng hướng với vectơ $\overrightarrow{EF}$ và $\left|\overrightarrow{DB}\right|=\left|\overrightarrow{C\text{D}}\right|=\left|\overrightarrow{EF}\right|=\frac{BC}{2}$.

Do đó các vectơ bằng vectơ $\overrightarrow{EF}$ là vectơ $\overrightarrow{DB}$ và vectơ $\overrightarrow{CD}$.

b) Tứ giác FECD có EF // CD và EF = CD nên FECD là hình bình hành.

Do đó EC = FD.

Do E là trung điểm của AC nên EA = EC.

Ta thấy các vectơ $\overrightarrow{E\text{A}}$, vectơ $\overrightarrow{DF}$ và vectơ $\overrightarrow{CE}$ ngược hướng với vectơ $\overrightarrow{EC}$ và

$\left|\overrightarrow{E\text{A}}\right|=\left|\overrightarrow{DF}\right|=\left|\overrightarrow{CE}\right|=\left|\overrightarrow{EC}\right|$.

Do đó các vectơ đối của vectơ $\overrightarrow{EC}$ là vectơ $\overrightarrow{E\text{A}}$, vectơ $\overrightarrow{DF}$ và vectơ $\overrightarrow{CE}$.

Thực hành 6 trang 86 Toán lớp 10 Tập 1: Tìm độ dài của các vectơ  $\overrightarrow{EF},\overrightarrow{EE},\overrightarrow{EM},\overrightarrow{MM},\overrightarrow{FF}$ trong Ví dụ 5.

Cho đoạn thẳng EF có độ dài bằng 2 và nhận M là trung điểm.

Lời giải:

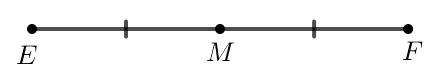
Do M là trung điểm của EF nên EM = $\frac{1}{2}$EF = 1.

Ta có: $\left|\overrightarrow{EF}\right|$ = EF = 2, $\left|\overrightarrow{EE}\right|=\left|\overrightarrow{0}\right|$ = 0, $\left|\overrightarrow{EM}\right|$ = EM = 1, $\left|\overrightarrow{MM}\right|=\left|\overrightarrow{0}\right|$ = 0, $\left|\overrightarrow{FF}\right|=\left|\overrightarrow{0}\right|$ = 0.

Bài 1 trang 86 Toán lớp 10 Tập 1: 

a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

- Bác Ba có số tiền là 20 triệu đồng.

- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.

b) Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?

Giá tiền, lực, thể tích, tuổi, độ dịch chuyển, vận tốc.

Lời giải:

a) - Đại lượng số tiền 20 triệu đồng biểu thị số tiền bác Ba có.

- Đại lượng vận tốc 20 km/h của cơn bão di chuyển theo hướng đông bắc biểu thị quãng đường cơn bão đi được mỗi giờ và hướng đi của cơn bão.

b) Các đại lượng giá tiền, thể tích, tuổi được biểu diễn bởi các số thực.

Do đó các đại lượng cần được biểu diễn bởi vectơ là: lực, độ dịch chuyển, vận tốc.

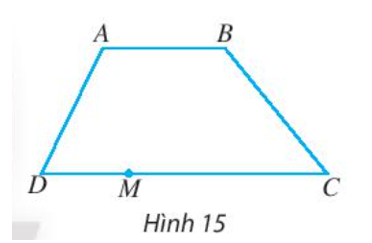
Bài 2 trang 86 Toán lớp 10 Tập 1: Cho hình thang ABCD có hai đáy là AB và DC (Hình 15). Điểm M nằm trên đoạn DC.

a) Gọi tên các vectơ cùng hướng với vectơ $\overrightarrow{AB}$.

b) Gọi tên các vectơ ngược hướng với vectơ $\overrightarrow{DM}$.

Lời giải:

a) Do ABCD là hình thang nên AB // CD.

Do đó các vectơ cùng hướng với vectơ $\overrightarrow{AB}$ là: vectơ $\overrightarrow{DM}$, vectơ $\overrightarrow{MC}$, vectơ $\overrightarrow{DC}$.

b) Các vectơ ngược hướng với vectơ $\overrightarrow{DM}$ là: vectơ $\overrightarrow{BA}$, vectơ $\overrightarrow{CM}$, vectơ $\overrightarrow{M\text{D}}$,

vectơ $\overrightarrow{CD}$.

Bài 3 trang 86 Toán lớp 10 Tập 1: Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16).

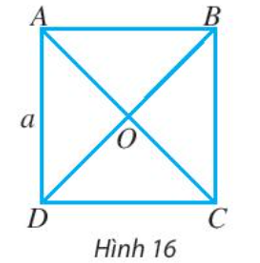
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng $\frac{a\sqrt{2}}{2}$.

b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng $a\sqrt{2}$.

Lời giải:

a) Hình vuông ABCD có tâm O nên AC $\perp$ BD và OA = OB = OC = OD.

Áp dụng định lí Pythagore vào tam giác AOD vuông tại O có:

OA² + OD² = AD²

$\Rightarrow$ 2OA² = a²

$\Rightarrow$ OA² = $\frac{a^2}{2}$

$\Rightarrow$ OA = $\frac{a}{\sqrt{2}}=\frac{a\sqrt{2}}{2}$ (do OA là độ dài đoạn thẳng nên OA > 0)

Ta thấy hai vectơ $\overrightarrow{OA}$ và $\overrightarrow{CO}$ cùng hướng và $\left|\overrightarrow{OA}\right|=\left|\overrightarrow{CO}\right|$ nên hai vectơ bằng nhau và có độ dài bằng $\frac{a\sqrt{2}}{2}$ là vectơ $\overrightarrow{OA}$ và vectơ $\overrightarrow{CO}$.

Chú ý: Ngoài ra chúng ta có thể có hai vectơ bằng nhau và có độ dài bằng $\frac{a\sqrt{2}}{2}$ là vectơ $\overrightarrow{OB}$ và vectơ $\overrightarrow{DO}$, …

b) Áp dụng định lí Pythagore vào tam giác ADC vuông tại D:

AD² + DC² = AC²

$\Rightarrow$ a² + a² = AC²

$\Rightarrow$ AC² = 2a²

$\Rightarrow$ AC = $\sqrt{2}$a (do AC là độ dài đoạn thẳng nên AC > 0)

Ta thấy hai vectơ $\overrightarrow{AC}$ và $\overrightarrow{CA}$ ngược hướng và $\left|\overrightarrow{AC}\right|=\left|\overrightarrow{CA}\right|$ nên hai vectơ bằng nhau và có độ dài bằng $a\sqrt{2}$ là vectơ $\overrightarrow{AC}$ và vectơ $\overrightarrow{CA}$.

Chú ý: Ngoài ta chúng ta có thể có hai vectơ bằng nhau và có độ dài bằng $a\sqrt{2}$ là vectơ $\overrightarrow{B\text{D}}$ và vectơ $\overrightarrow{DB}$.

Bài 4 trang 86 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi $\overrightarrow{AB}=\overrightarrow{DC}$.

Lời giải:

Phần thuận: ABCD là hình bình hành thì $\overrightarrow{AB}=\overrightarrow{DC}$.

Do ABCD là hình hình bình hành nên AB = DC và AB // DC.

Khi đó ta thấy hai vectơ $\overrightarrow{AB}$ và vectơ $\overrightarrow{DC}$ cùng hướng.

Mà AB = DC nên $\overrightarrow{AB}=\overrightarrow{DC}$.

Phần đảo: Tứ giác ABCD có $\overrightarrow{AB}=\overrightarrow{DC}$ thì ABCD là hình bình hành.

Giá của vectơ $\overrightarrow{AB}$ là đường thẳng AB, giá của vectơ $\overrightarrow{DC}$ là đường thẳng DC.

Do $\overrightarrow{AB}=\overrightarrow{DC}$ nên đường thẳng AB và đường thẳng DC song song hoặc trùng nhau.

Do A, B, C, D là 4 đỉnh của tứ giác nên hai đường thẳng AB và DC không trùng nhau.

Do đó đường thẳng AB và đường thẳng DC song song với nhau.

Mà $\overrightarrow{AB}=\overrightarrow{DC}$ nên $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{DC}\right|$ hay AB = CD.

Tứ giác ABCD có AB // CD và AB = CD nên tứ giác ABCD là hình bình hành.

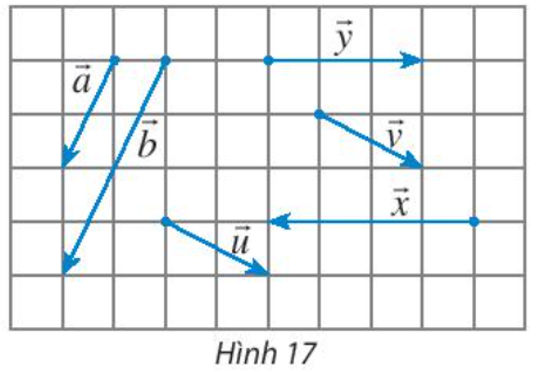
Bài 5 trang 86 Toán lớp 10 Tập 1: Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong Hình 17.

Lời giải:

Các cặp vectơ cùng hướng là: $\overrightarrow{a}$ và $\overrightarrow{b}$, $\overrightarrow{u}$ và $\overrightarrow{v}$.

Cặp vectơ ngược hướng là: $\overrightarrow{x}$ và $\overrightarrow{y}$.

Cặp vectơ bằng nhau là: $\overrightarrow{u}$ và $\overrightarrow{v}$.

Bài 6 trang 87 Toán lớp 10 Tập 1: Gọi O là tâm hình lục giác đều ABCDEF.

a) Tìm các vectơ khác vectơ $\overrightarrow{0}$ và cùng hướng với vectơ $\overrightarrow{OA}$.

b) Tìm các vectơ bằng vectơ $\overrightarrow{AB}$.

Lời giải:

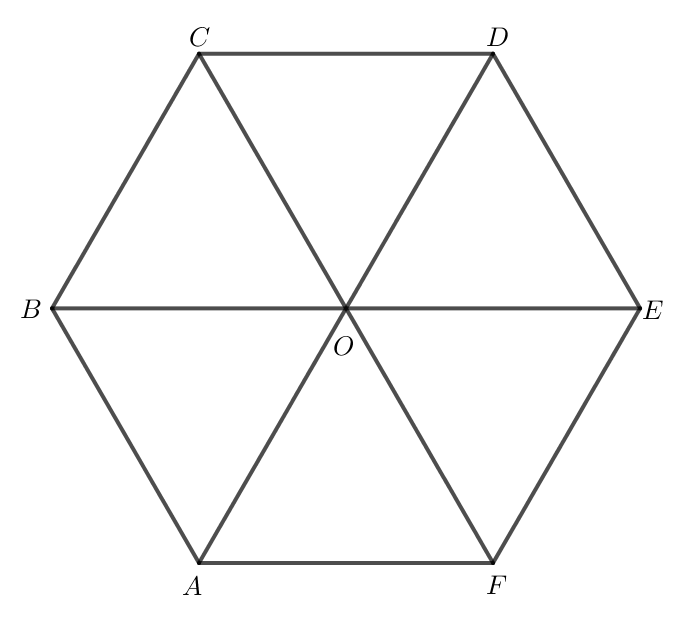
a) Do ABCDEF là lục giác đều nên BC // AD // EF.

Do đó các vectơ cùng hướng với vectơ $\overrightarrow{OA}$ là: vectơ $\overrightarrow{CB}$, vectơ $\overrightarrow{DO}$, vectơ $\overrightarrow{DA}$, vectơ $\overrightarrow{EF}$.

b) Do ABCDEF là lục giác đều nên AB // CF // DE và AB = OC = FO = ED.

Các vectơ $\overrightarrow{OC}$, vectơ $\overrightarrow{F\text{O}}$, vectơ $\overrightarrow{E\text{D}}$ cùng hướng với vectơ $\overrightarrow{AB}$ và

$\left|\overrightarrow{OC}\right|=\left|\overrightarrow{F\text{O}}\right|=\left|\overrightarrow{E\text{D}}\right|=\left|\overrightarrow{AB}\right|$ nên các vectơ bằng vectơ $\overrightarrow{AB}$ là: vectơ $\overrightarrow{OC}$, vectơ $\overrightarrow{F\text{O}}$ và

vectơ $\overrightarrow{E\text{D}}$.

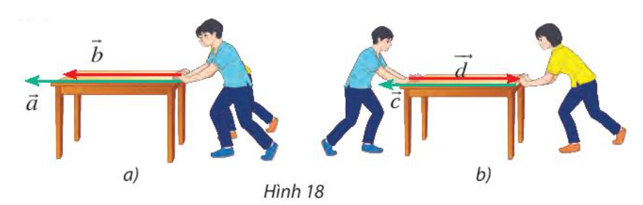
Bài 7 trang 87 Toán lớp 10 Tập 1: Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong Hình 18.

Lời giải:

Trong Hình 18a ta thấy hai lực $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.

Trong Hình 18b ta thấy hai lực $\overrightarrow{c}$ và $\overrightarrow{d}$ ngược hướng.

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: