Hàm số $y=2x^3-9x^2+12x+3$ nghịch biến trên những khoảng nào?

I. Tính đơn điệu của hàm số

1. Nhắc lại định nghĩa

- Định nghĩa:

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:

Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) nhỏ hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) < f(x₂).

Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) lớn hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) > f(x₂).

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

- Nhận xét: Từ định nghĩa trên ta thấy:

a) f(x) đồng biến trên K $\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0;\forall x_1;x_2\in K;(x_1\ne x_2)$.

f(x) nghịch biến trên K $\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}<\mathrm{\hspace{0.17em}0};\forall x_1;x_2\in K;(x_1\ne x_2)$.

b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

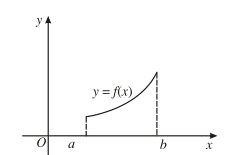
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

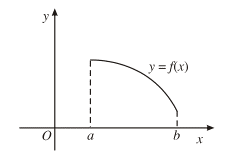
2. Tính đơn điệu và dấu của đạo hàm

- Định lí:

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

- Chú ý:

Nếu f’(x) = 0 với $\forall x\in K$ thì f(x) không đổi trên K.

Ví dụ 1. Tìm các khoảng đơn điệu của hàm số

a) y = x² + 2x – 10;

b) $y=\frac{x+\mathrm{\hspace{0.17em}5}}{2x-3}$.

Lời giải:
a) Hàm số đã cho xác định với mọi x$\in R$.

Ta có  đạo hàm y’ = 2x + 2

Và y’ = 0 khi x = – 1.

Lập bảng biến thiên:

 Vậy hàm số đã cho đồng biến trên khoảng $(-1;+\mathrm{\infty })$ và  nghịch biến trên khoảng $(-\mathrm{\infty };-1)$.

b) $y=\frac{x+\mathrm{\hspace{0.17em}5}}{2x-3}$

Hàm số đã cho xác định với $\forall x\ne \frac{3}{2}$

Ta có: $y^{\text{'}}=\frac{-13}{{(2x-3)}^2}<0\forall x\ne \frac{3}{2}$

Do đó, hàm số đã cho nghịch biến trên khoảng $(-\mathrm{\infty };\frac{3}{2})$ và $(\frac{3}{2};+\mathrm{\infty })$.

 - Chú ý:

Ta có định lí mở rộng sau đây:

Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu $f^{\text{'}}\left(x\right)\ge 0(f^{\text{'}}\left(x\right)\le 0);\forall x\in K$

Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

Ví dụ 2.  Tìm các khoảng đơn điệu của hàm số y = x³ – 6x² + 12x – 10.

Lời giải:

Hàm số đã cho xác định với mọi x$\in R$.

Ta có: y’ = 3x² – 12x + 12 = 3(x – 2)²

Do đó; y’ = 0 khi x = 2 và y’ > 0 với $\forall x\ne 2$.

Theo định lí mở rộng, hàm số đã cho luôn luôn đồng biến trên \(\mathbb{R}\).

II. Quy tắc xét tính đơn điệu của hàm số.

1. Quy tắc

- Bước 1. Tìm tập xác định.

- Bước 2. Tính đạo hàm  f’(x). Tìm các điểm x_i  ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

- Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

- Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

2. Áp dụng

Ví dụ 3. Xét sự đồng biến, nghịch biến của hàm số y = x⁴ – 2x² – 3.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = 4x³ – 4x

y’ = 0 $\iff [\begin{array}{c}x=0\\ x=\pm 1\end{array}$

Bảng biến thiên:

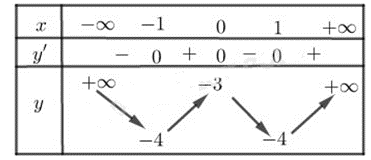
Vậy hàm số đã cho đồng biến trên (– 1; 0) và $(1;+\mathrm{\infty })$

Hàm số nghịch biến trên $(-\mathrm{\infty };-1)$ và (0; 1).

Ví dụ 4.  Cho hàm số $y=-x^3+6x^2-\mathrm{\hspace{0.17em}\hspace{0.17em}9}x+\mathrm{\hspace{0.17em}3}$. Xét tính đồng biến, nghịch biến của hàm số trên.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = – 3x² + 12x – 9

Và y’ = 0 $\iff [\begin{array}{c}x=\mathrm{\hspace{0.17em}\hspace{0.17em}1}\\ x=\mathrm{\hspace{0.17em}3}\end{array}$

Bảng biến thiên:

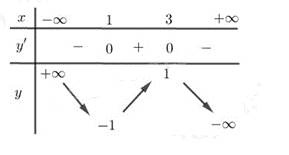
Vậy hàm số đã cho đồng biến trên (1; 3); nghịch biến trên $(-\mathrm{\infty };\mathrm{\hspace{0.17em}\hspace{0.17em}1})$ và $(3;+\mathrm{\infty })$.