Điều kiện để hàm số y = ax⁴ +bx² + c $(a\ne \mathrm{0)}$  có 3 điểm cực trị là

I. Khái niệm cực đại, cực tiểu.

- Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là $-\mathrm{\infty }$; b là $+\mathrm{\infty })$ và điểm x₀ $\in$(a; b).

a) Nếu tồn tại số h > 0 sao cho f(x) < f(x₀) với mọi x$\in$ (x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực đại tại x₀.

b) Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x$\in$(x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

- Chú ý:

1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.

Kí hiệu là f_CĐ (f_CT) còn điểm M(x₀; f(x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x₀ thì f’(x₀) = 0.

II. Điều kiện đủ để hàm số có cực trị

- Định lí 1

Giả sử hàm số y = f(x) liên tục trên khoảng K = (x₀ – h; x₀ + h) và có đạo hàm trên K  hoặc trên K \ {x₀}; với h > 0.

a) Nếu f’(x) > 0 trên khoảng (x₀ – h; x₀) và f’(x) < 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x).

b) Nếu f’(x) < 0 trên khoảng (x₀ – h; x₀) và f’(x) > 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x).

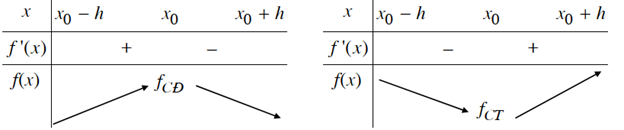
Ví dụ 1. Tìm các điểm cực trị của hàm số y = – 2x³ + 3x².

Lời giải:

Hàm số xác định với mọi x.

Ta có: y’ = – 6x² + 6x

Và y’ = 0 $\iff [\begin{array}{c}x=0\\ x=1\end{array}$

Bảng biến thiên:

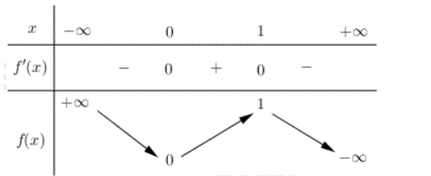
Từ bảng biến thiên, suy ra x = 0 là điểm cực tiểu của hàm số và x = 1 là điểm cực đại của hàm số.

Ví dụ 2. Tìm các điểm cực trị của hàm số $y=\frac{2-x}{2x+\mathrm{\hspace{0.17em}2}}$.

Lời giải:

Hàm số đã cho xác định với $\forall x\ne -1$.

Ta có: $y^{\text{'}}=\frac{-6}{{(2x+2)}^2}<0$

Vậy hàm số đã cho không có cực trị (vì theo khẳng định 3 của chú ý trên, nếu hàm số đạt cực trị tại x₀ thì y’(x₀) = 0).

III. Quy tắc tìm cực trị .

- Quy tắc 1.

1. Tìm tập xác định.

2. Tính f’(x). Tìm các điểm tại đó f’(x) bằng 0 hoặc f’(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

- Định lí 2.

Giả sử hàm số y = f(x) có đạo  hàm cấp hai trong khoảng (x₀ – h; x₀ + h) với h > 0. Khi đó:

a) Nếu f’(x₀) = 0; f”(x₀) > 0 thì x₀ là điểm cực tiểu;

b) Nếu f’(x₀) = 0; f”(x₀) < 0 thì x₀ là điểm cực đại.

- Quy tắc II.

1. Tìm tập xác định

2. Tính f’(x). Giải phương trình f’(x) = 0 và kí hiệu x_i ( i = 1; 2; ….; n) là các nghiệm của nó.

3. Tính f”(x) và f”(x_i).

4. Dựa vào dấu của f”(x_i) suy ra tính chất cực trị của điểm x_i.

- Ví dụ 4. Tìm cực trị của hàm số $f\left(x\right)=x^4-\mathrm{\hspace{0.17em}\hspace{0.17em}2}{x}^2+\mathrm{\hspace{0.17em}\hspace{0.17em}10}$.

Lời giải:

Hàm số đã cho xác định với mọi x

Ta có: f’(x) = 4x³ – 4x

$f^{\text{'}}\left(x\right)=0\iff [\begin{array}{c}x=0\\ x=\pm 1\end{array}$

Ta có: f”(x) = 12x² – 4

Suy ra: f”(0) = – 4 < 0 nên x = 0 là điểm cực đại.

f”(1) = f”(– 1)  = 8 > 0 nên x = 1 và x = –1 là điểm cực tiểu.

Kết luận:

Hàm số f(x) đạt cực tiểu tại x = 1 và x = – 1; f_CT = f(1) = f(–1) = 9.

Hàm số f(x) đạt cực đại tại x = 0 và f_CD = f(0) = 10.