Cho tam giác ABC có AB = AC. Trên hai cạnh AB và AC lần lượt lấy 2 điểm M và N sao cho AM = AN. Gọi D, E lần lượt là trung điểm của MN và BC. Chứng minh rằng: 3 điểm A, E, D thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
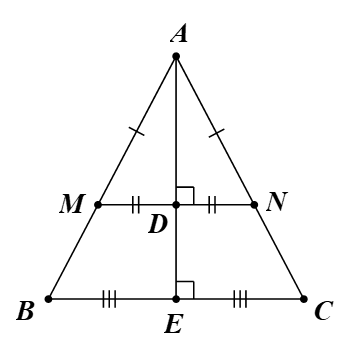
Tam giác ABC có AB = AC (giả thiết).
Suy ra tam giác ABC cân tại A.
Do đó đường trung tuyến AE cũng là đường phân giác của tam giác ABC.
Vì vậy AE là tia phân giác của \(\widehat {BAC}\) (1)
Chứng minh tương tự, ta được AD là tia phân giác của \(\widehat {BAC}\) (2)
Từ (1), (2), ta thu được ba điểm A, E, D thẳng hàng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho nửa đường tròn tâm O, đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại O.
b) Chứng minh AC.BD = R2.
c) Kẻ MH vuông góc với AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.
Cho đường tròn (O) và điểm A bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). AC cắt đường tròn (O) tại D (D khác C).
a) Chứng minh rằng BD vuông góc AC và AB2 = AD.AC.
b) Từ C vẽ dây CE // OA. BE cắt OA tại H. Chứng minh rằng H là trung điểm của BE và AE là tiếp tuyến.
c) Chứng minh rằng \(\widehat {OCH} = \widehat {OAC}\).
d) Tia OA cắt đường tròn tại F. Chứng minh rằng FA.CH = HF.CA.
Cho đường tròn (O) và điểm A ngoài (O). Qua A kẻ các tiếp tuyến AB, AC với (O) trong đó B, C là các tiếp điểm. Lấy M là điểm thuộc cung nhỏ BC. Tiếp tuyến qua M với (O) cắt AB, AC lần lượt tại D và E. Chứng minh:
a) Chu vi tam giác ADE bằng 2AB.
b) \(\widehat {DOE} = \frac{1}{2}\widehat {BOC}\).
Một lớp học có 30 học sinh gồm cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được 2 nữ và 1 nam là \(\frac{{52}}{{145}}\). Tính số học sinh nữ của lớp.
Cho tứ giác ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Gọi G, G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó \(\overrightarrow {GG'} \) bằng:
Có 8 cái bút khác nhau và 9 quyển vở khác nhau được gói trong 17 hộp. Một học sinh được chọn bất kì hai hộp. Xác suất để học sinh đó chọn được một cặp bút và vở là
Một lớp học có 30 học sinh gồm cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được 2 nam và 1 nữ là \(\frac{{12}}{{29}}\). Tính số học sinh nữ của lớp.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với đáy và góc tạo bởi SB với đáy (ABC) bằng 60°. Tính thể tích khối chóp S.ABC tính theo a.
Cho tam giác ABC vuông tại B, đường trung tuyến BM, đường cao BH. Lấy E đối xứng với B qua M.
a) Chứng minh tứ giác ABCE là hình chữ nhật.
b) Qua E kẻ đường thẳng song song với AC cắt BC tại D, cắt BH tại I. Chứng minh tứ giác ACDE là hình bình hành.
c) Chứng minh EI // AM.
d) Chứng minh tứ giác AIEC là hình thang cân.
e) Tam giác ABC cần thêm điều kiện gì để ABCE là hình vuông?
Tìm một số tự nhiên có 3 chữ số, biết rằng khi viết thêm chữ số 2 vào bên phải số đó thì nó tăng 4106 đơn vị.
Lấy điểm A trên (O; R), vẽ tiếp tuyến Ax. Trên Ax lấy điểm B. Trên (O; R) lấy điểm C sao cho BC = AB.
a) Chứng minh CB là tiếp tuyến của (O).
b) Vẽ đường kính AD của (O), kẻ CK vuông góc với AD. Chứng minh rằng CD // OB và BC.CD = CK.OB.
c) Lấy điểm M trên cung nhỏ AC của (O). Vẽ tiếp tuyến tại M cắt AB, BC lần lượt tại E, F. Vẽ đường tròn tâm I nội tiếp ∆BEF. Chứng minh .
Cho hình thoi ABCD, có O là giao điểm của hai đường chéo AC và BD. Lấy điểm M, N lần lượt là trung điểm của cạnh AD, CD.
a) Nêu nhận xét về quan hệ bằng nhau của \(\widehat {ABD}\) và \(\widehat {ADB}\). Vì sao?
b) Tứ giác AMNC là hình gì? Vì sao?
c) Chứng minh tứ giác OMDN là hình thoi.
d) Gọi E là giao điểm của đường thẳng BM với đường thẳng CD. Tính số đo \(\widehat {AED}\), biết \(\widehat {BAD} = 130^\circ \).
Cho tam giác ABC có BC = a, CA = b, AB = c thỏa mãn \[\frac{{a + b}}{6} = \frac{{b + c}}{5} = \frac{{c + a}}{7}\]. Tính giá trị của biểu thức T = cosA + 2cosB + 3cosC.
Trong các số thập phân 86,42; 86,422; 686,42; 86,642. Số thập phân lớn nhất là
Tìm m để các hàm số sau có tập xác định là ℝ (hay luôn xác định trên ℝ):
a) \(y = f\left( x \right) = \frac{{3x + 1}}{{{x^2} + 2\left( {m - 1} \right)x + {m^2} + 3m + 5}}\).
b) \(y = f\left( x \right) = \sqrt {{x^2} + 2\left( {m - 1} \right)x + {m^2} + m - 6} \).
c) \(y = f\left( x \right) = \frac{{3x + 5}}{{\sqrt {{x^2} - 2\left( {m + 3} \right)x + m + 9} }}\).