Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 71)
-
912 lượt thi
-
42 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Rút gọn biểu thức: 2x(x – 4)2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)2 – (x – 1)2.
 Xem đáp án
Xem đáp án
Ta có 2x(x – 4)2 – (x + 5)(x – 2)(x + 2) + 2(x + 5)2 – (x – 1)2
= 2x(x2 – 8x + 16) – (x + 5)(x2 – 4) + 2(x2 + 10x + 25) – (x2 – 2x + 1)
= 2x3 – 16x2 + 32x – (x3 – 4x + 5x2 – 20) + 2x2 + 20x + 50 – x2 + 2x – 1
= (2x3 – x3) + (–16x2 – 5x2 + 2x2 – x2) + (32x + 4x + 20x + 2x) + (20 + 50 – 1)
= x3 – 20x2 + 58x + 69.
Câu 2:
Cho biết tích của hai số tự nhiên n và m là 36. Mỗi tích n.(–m) và (–n).(–m) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Vì tích của hai số tự nhiên n và m là 36 nên n.m = 36.
Ta có:
⦁ n.(–m) = –(n.m) = –36.
⦁ (–n).(–m) = n.m = 36.
Vậy n.(–m) = –36 và (–n).(–m) = 36.
Câu 3:
Cho a, b, c đôi một khác nhau và khác 0 thỏa mãn (a + b + c)2 = a2 + b2 + c2. Tính giá trị biểu thức \(A = \frac{{{a^2}}}{{{a^2} + 2bc}} + \frac{{{b^2}}}{{{b^2} + 2ca}} + \frac{{{c^2}}}{{{c^2} + 2ab}}\).
 Xem đáp án
Xem đáp án
Ta có (a + b + c)2 = a2 + b2 + c2.
⇔ a2 + b2 + c2 + 2(ab + bc + ca) = a2 + b2 + c2.
⇔ 2(ab + bc + ca) = 0.
⇔ ab + bc + ca = 0.
⇔ bc = –ab – ca.
Suy ra \(\frac{{{a^2}}}{{{a^2} + 2bc}} = \frac{{{a^2}}}{{{a^2} + bc - ab - ac}} = \frac{{{a^2}}}{{a\left( {a - b} \right) - c\left( {a - b} \right)}} = \frac{{{a^2}}}{{\left( {a - c} \right)\left( {a - b} \right)}}\).
Chứng minh tương tự, ta được \(\frac{{{b^2}}}{{{b^2} + 2ca}} = \frac{{{b^2}}}{{\left( {b - a} \right)\left( {b - c} \right)}}\); \(\frac{{{c^2}}}{{{c^2} + 2ab}} = \frac{{{c^2}}}{{\left( {a - c} \right)\left( {b - c} \right)}}\).
Khi đó ta có \(A = \frac{{{a^2}}}{{{a^2} + 2bc}} + \frac{{{b^2}}}{{{b^2} + 2ca}} + \frac{{{c^2}}}{{{c^2} + 2ab}}\).
\( = \frac{{{a^2}}}{{\left( {a - c} \right)\left( {a - b} \right)}} + \frac{{{b^2}}}{{\left( {b - a} \right)\left( {b - c} \right)}} + \frac{{{c^2}}}{{\left( {a - c} \right)\left( {b - c} \right)}}\).
\( = \frac{{{a^2}\left( {b - c} \right) - {b^2}\left( {a - c} \right) + {c^2}\left( {a - b} \right)}}{{\left( {a - c} \right)\left( {a - b} \right)\left( {b - c} \right)}}\).
\( = \frac{{{a^2}b - {a^2}c - {b^2}a + {b^2}c + {c^2}\left( {a - b} \right)}}{{\left( {a - c} \right)\left( {a - b} \right)\left( {b - c} \right)}}\).
\( = \frac{{ab\left( {a - b} \right) - c\left( {a - b} \right)\left( {a + b} \right) + {c^2}\left( {a - b} \right)}}{{\left( {a - c} \right)\left( {a - b} \right)\left( {b - c} \right)}}\).
\( = \frac{{\left( {a - b} \right)\left( {ab - ca - cb + {c^2}} \right)}}{{\left( {a - c} \right)\left( {a - b} \right)\left( {b - c} \right)}}\).
\( = \frac{{\left( {a - b} \right)\left( {b - c} \right)\left( {a - c} \right)}}{{\left( {a - c} \right)\left( {a - b} \right)\left( {b - c} \right)}} = 1\).
Vậy A = 1.
Câu 4:
Cho \(\cot a = \frac{1}{2}\). Tính giá trị biểu thức sin2a.cosa + cosa.
 Xem đáp án
Xem đáp án
Vì tana.cota = 1 nên \(\tan a = \frac{1}{{\cot a}} = 2\).
Suy ra cosa ≠ 0.
Ta có \({\sin ^2}a.\cos a + \cos a = \frac{{{{\sin }^2}a.\cos a}}{{{{\cos }^3}a}} + \frac{{\cos a}}{{{{\cos }^3}a}} = \frac{{{{\sin }^2}a}}{{{{\cos }^2}a}} + \frac{1}{{{{\cos }^2}a}}\).
= tan2a + 1 + tan2a = 2tan2a + 1 = 2.22 + 1 = 9.
Vậy sin2a.cosa + cosa = 9.
Câu 5:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60°. Gọi (S) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Câu 6:
Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Chứng minh rằng nếu ABCD là hình thang cân thì MP là tia phân giác của \[\widehat {QMN}\].
 Xem đáp án
Xem đáp án
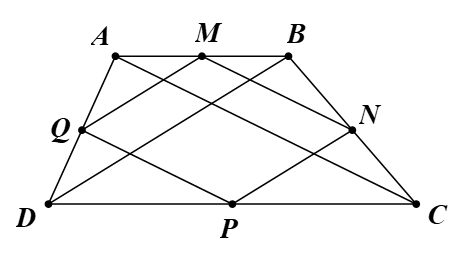
a) Tam giác ABD có M, Q lần lượt là trung điểm của AB, AD.
Suy ra MQ là đường trung bình của tam giác ABD.
Do đó MQ // BD và \(MQ = \frac{1}{2}BD\) (1)
Chứng minh tương tự, ta được NP // BD và \(NP = \frac{1}{2}BD\) (2)
Từ (1), (2), suy ra MQ // NP và MQ = NP.
Vậy tứ giác MNPQ là hình bình hành.
b) Tam giác ABC có M, N lần lượt là trung điểm của AB, BC.
Suy ra MN là đường trung bình của tam giác ABC.
Do đó \(MN = \frac{1}{2}AC\).
Nếu ABCD là hình thang cân thì AC = BD.
Mà \(MQ = \frac{1}{2}BD\) (chứng minh trên) và \(MN = \frac{1}{2}AC\) (chứng minh trên).
Suy ra MQ = MN.
Mà tứ giác MNPQ là hình bình hành.
Do đó tứ giác MNPQ là hình thoi.
Vậy MP là là tia phân giác của \[\widehat {QMN}\].
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho điểm M(4; 1), đường thẳng d luôn đi qua M, d cắt Ox, Oy lần lượt tại A(a; 0), B(0; b). Hãy viết phương trình đường thẳng (d) sao cho SOAB = 2.
 Xem đáp án
Xem đáp án
Phương trình đường thẳng d có dạng: \(\frac{x}{a} + \frac{y}{b} = 1\) (theo giả thiết, ta có a > 0, b > 0).
Vì d luôn đi qua M(4; 1) nên ta có \(\frac{4}{a} + \frac{1}{b} = 1\).
⇔ 4b + a = ab (1)
Ta có OA = |a|, OB = |b|.
Suy ra \({S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}\left| {ab} \right|\).
Theo đề, ta có SOAB = 2.
\( \Leftrightarrow \frac{1}{2}\left| {ab} \right| = 2\).
⇔ |ab| = 4.
⇔ ab = 4 hoặc ab = –4.
Thế \(ab = 4 \Leftrightarrow a = \frac{4}{b}\) vào (1), ta được: \(4b + \frac{4}{b} = 4\).
⇔ 4b2 – 4b + 4 = 0 (vô nghiệm).
Thế \(ab = - 4 \Leftrightarrow a = - \frac{4}{b}\) vào (1), ta được: \(4b - \frac{4}{b} = - 4\).
⇔ 4b2 + 4b – 4 = 0.
\( \Leftrightarrow b = \frac{{ - 1 \pm \sqrt 5 }}{2}\).
Với \(b = \frac{{ - 1 + \sqrt 5 }}{2}\), ta có \(a = - \frac{4}{b} = - 2 - 2\sqrt 5 \).
Với \(b = \frac{{ - 1 - \sqrt 5 }}{2}\), ta có \(a = - \frac{4}{b} = - 2 + 2\sqrt 5 \).
Vậy có hai đường thẳng d thỏa mãn yêu cầu bài toán có phương trình là \(\left( { - 1 + \sqrt 5 } \right)x - 4\left( {1 + \sqrt 5 } \right)y + 8 = 0\) và \[\left( {1 + \sqrt 5 } \right)x + 4\left( {1 - \sqrt 5 } \right)y - 8 = 0\].
Câu 8:
Cho nửa đường tròn tâm O, đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại O.
b) Chứng minh AC.BD = R2.
c) Kẻ MH vuông góc với AB (H ∈ AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH.
 Xem đáp án
Xem đáp án
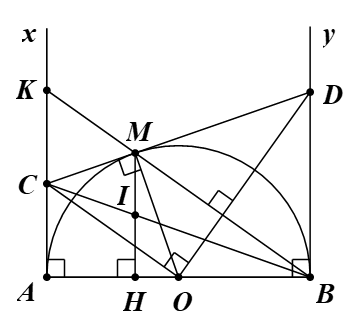
a) Đường tròn (O) có hai tiếp tuyến AC, MC cắt nhau tại C.
Suy ra OC là tia phân giác của \(\widehat {AOM}\) (tính chất hai tiếp tuyến cắt nhau).
Do đó \(2\widehat {AOC} = 2\widehat {COM} = \widehat {AOM}\).
Chứng minh tương tự, ta được \(2\widehat {MOD} = 2\widehat {DOB} = \widehat {MOB}\).
Ta có \(\widehat {AOM} + \widehat {MOB} = 180^\circ \) (kề bù).
Suy ra \(2\widehat {COM} + 2\widehat {MOD} = 180^\circ \).
Khi đó \(2\left( {\widehat {COM} + \widehat {MOD}} \right) = 180^\circ \).
Vì vậy \(\widehat {COD} = 180^\circ :2 = 90^\circ \).
Vậy tam giác COD vuông tại O.
b) Đường tròn (O) có hai tiếp tuyến AC, MC cắt nhau tại C.
Suy ra AC = MC (tính chất hai tiếp tuyến cắt nhau).
Chứng minh tương tự, ta được DM = BD.
Ta có CD là tiếp tuyến của (O) có M là tiếp điểm. Suy ra OM ⊥ CD.
Tam giác COD vuông tại O có OM là đường cao: OM2 = CM.DM.
⇔ R2 = AC.BD.
Vậy ta có điều phải chứng minh.
c) Gọi I là giao điểm của MH và BC, K là giao điểm của MB và AC.
Đường tròn (O) có hai tiếp tuyến DM, DB cắt nhau tại D.
Suy ra DM = DB.
Lại có OM = OB = R.
Suy ra OD là đường trung trực của đoạn MB.
Do đó OD ⊥ MB.
Mà OD ⊥ OC (tam giác COD vuông tại O).
Suy ra MB // OC.
Mà O là trung điểm AB (đường tròn (O) có AB là đường kính).
Do đó OC là đường trung bình của tam giác ABK.
Vì vậy C là trung điểm AK.
Ta có MH ⊥ AB (giả thiết) và AK ⊥ AB (do AK là tiếp tuyến của (O) tại A).
Suy ra MH // AK.
Áp dụng định lí Thales, ta được \(\frac{{MI}}{{CK}} = \frac{{IH}}{{AC}} = \frac{{BI}}{{BC}}\).
Mà CK = CA (C là trung điểm AK).
Suy ra MI = IH.
Do đó I là trung điểm của MH.
Vậy BC đi qua trung điểm I của đoạn MH.
Câu 9:
Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE.
c) Cho AB = 10 cm, BC = 12 cm. Tính diện tích tam giác OAD.
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân.
 Xem đáp án
Xem đáp án
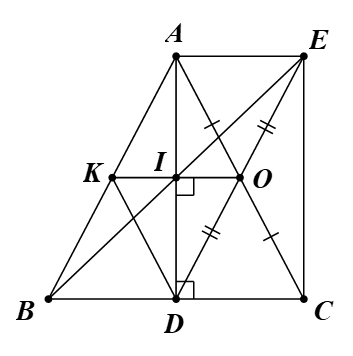
a) Tứ giác AECD, có hai đường chéo AC và DE cắt nhau tại O.
Mà O là trung điểm của AC (giả thiết) và O cũng là trung điểm của DE (điểm E đối xứng với điểm D qua điểm O).
Suy ra tứ giác AECD là hình bình hành.
Lại có \[\widehat {ADC} = 90^\circ \] (AD ⊥ BC).
Vậy tứ giác AECD là hình chữ nhật.
b) Tam giác ABC cân tại A có AD vừa là đường cao, vừa là đường trung tuyến.
Suy ra D là trung điểm BC.
Do đó BD = CD (1)
Vì AECD là hình chữ nhật nên AE // CD và AE = CD (2)
Từ (1), (2), suy ra AE = BD.
Tứ giác AEDB, có: AE // BD và AE = CD (chứng minh trên).
Suy ra tứ giác AEDB là hình bình hành.
Mà I là trung điểm của AD.
Vậy I cũng là trung điểm của BE.
c) Ta có D là trung điểm BC. Suy ra \(BD = CD = \frac{{BC}}{2} = \frac{{12}}{2} = 6\) (cm).
Tam giác ACD có O, I lần lượt là trung điểm của AC, AD.
Suy ra OI là đường trung bình của tam giác ACD.
Do đó OI // CD và \(OI = \frac{{CD}}{2} = \frac{6}{2} = 3\) (cm).
Tam giác ABD vuông tại D: AD2 = AB2 – BD2 = 102 – 62 = 64.
Suy ra AD = 8 (cm).
Ta có OI // CD (chứng minh trên) và CD ⊥ AD (tam giác ABC có AD là đường cao).
Suy ra OI ⊥ AD.
Diện tích tam giác OAD là: \({S_{\Delta OAD}} = \frac{1}{2}OI.AD = \frac{1}{2}.3.8 = 12\,\,\left( {c{m^2}} \right)\).
Vậy diện tích tam giác OAD bằng 12 cm2.
d) Vì tứ giác AEDB là hình bình hành nên AK // DE.
Suy ra tứ giác AEDK là hình thang.
Do đó để AKDE là hình thang cân thì \(\widehat {AED} = \widehat {KDE}\) (hai góc kề một đáy bằng nhau).
Ta có tứ giác AEDB là hình bình hành (chứng minh trên).
Suy ra OD // AK (3)
Tam giác ABC có OK // BC (chứng minh trên) và O là trung điểm AC (giả thiết).
Suy ra OK là đường trung bình của tam giác ABC.
Do đó K là trung điểm của AB.
Tam giác ABC có D, K lần lượt là trung điểm của BC, AB.
Suy ra DK là đường trung bình của tam giác ABC.
Do đó DK // AO (4)
Từ (3), (4), suy ra tứ giác AODK là hình bình hành.
Khi đó \(\widehat {KAO} = \widehat {KDO}\) (hai góc đối nhau).
Mà \(\widehat {AED} = \widehat {ABD}\) (hai góc đối nhau trong hình bình hành AEDB).
Do đó nếu \(\widehat {AED} = \widehat {KDE}\) thì \(\widehat {ABD} = \widehat {KAO}\).
Mà \(\widehat {ABC} = \widehat {ACB}\) (tam giác ABC cân tại A).
Suy ra \[\widehat {BAC} = \widehat {ABC} = \widehat {ACB}\].
Khi đó tam giác ABC đều.
Vậy tam giác ABC là tam giác đều thì tứ giác AEDK là hình thang cân.
Câu 10:
Cho tam giác ABC có AB = AC. Trên hai cạnh AB và AC lần lượt lấy 2 điểm M và N sao cho AM = AN. Gọi D, E lần lượt là trung điểm của MN và BC. Chứng minh rằng: 3 điểm A, E, D thẳng hàng.
 Xem đáp án
Xem đáp án
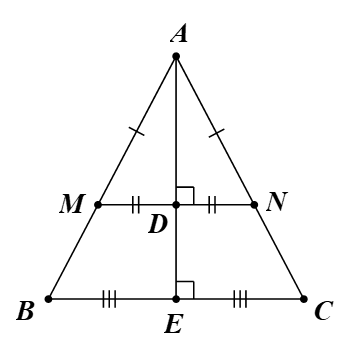
Tam giác ABC có AB = AC (giả thiết).
Suy ra tam giác ABC cân tại A.
Do đó đường trung tuyến AE cũng là đường phân giác của tam giác ABC.
Vì vậy AE là tia phân giác của \(\widehat {BAC}\) (1)
Chứng minh tương tự, ta được AD là tia phân giác của \(\widehat {BAC}\) (2)
Từ (1), (2), ta thu được ba điểm A, E, D thẳng hàng.
Câu 11:
Cho tam giác ABC có BC = a, CA = b, AB = c thỏa mãn \[\frac{{a + b}}{6} = \frac{{b + c}}{5} = \frac{{c + a}}{7}\]. Tính giá trị của biểu thức T = cosA + 2cosB + 3cosC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có \(\left\{ \begin{array}{l}\frac{{a + b}}{6} = \frac{{b + c}}{5}\\\frac{{a + b}}{6} = \frac{{c + a}}{7}\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}5a = b + 6c\\a + 7b = 6c\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}5a = b + a + 7b\\a + 7b = 6c\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}b = \frac{a}{2}\\a + 7.\frac{a}{2} = 6c\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}b = \frac{a}{2}\\c = \frac{{3a}}{4}\end{array} \right.\)
Khi đó ta có:
⦁ \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{3a}}{4}} \right)}^2} - {a^2}}}{{2.\frac{a}{2}.\frac{{3a}}{4}}} = - \frac{1}{4}\).
⦁ \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{a^2} + {{\left( {\frac{{3a}}{4}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}}}{{2a.\frac{{3a}}{4}}} = \frac{7}{8}\).
⦁ \(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{{a^2} + {{\left( {\frac{a}{2}} \right)}^2} - {{\left( {\frac{{3a}}{4}} \right)}^2}}}{{2a.\frac{a}{2}}} = \frac{{11}}{{16}}\).
Vì vậy \(T = \cos A + 2\cos B + 3\cos C = - \frac{1}{4} + 2.\frac{7}{8} + 3.\frac{{11}}{{16}} = \frac{{57}}{{16}}\).
Vậy ta chọn phương án A.
Câu 12:
Cho tam giác ABC cân tại A có \(\widehat A = 120^\circ \) và AB = a. Tính \(\overrightarrow {BA} .\overrightarrow {CA} \).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì tam giác ABC cân tại A nên AC = AB = a.
Ta có \(\overrightarrow {BA} .\overrightarrow {CA} = BA.CA.\cos \left( {\overrightarrow {BA} ,\overrightarrow {CA} } \right) = BA.CA.\cos \widehat {BAC} = a.a.\cos 120^\circ = - \frac{{{a^2}}}{2}\).
Vậy ta chọn phương án B.
Câu 13:
Cho tứ giác ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Gọi G, G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Khi đó \(\overrightarrow {GG'} \) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
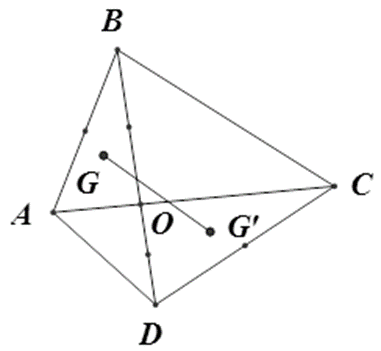
Vì G là trọng tâm của tam giác OAB nên \(\overrightarrow {GO} + \overrightarrow {GA} + \overrightarrow {GB} = \vec 0\).
\[ \Rightarrow \overrightarrow {GO} = - \overrightarrow {GA} - \overrightarrow {GB} \].
Ta có G’ là trọng tâm của tam giác OCD.
Suy ra \(\overrightarrow {GG'} = \frac{1}{3}\left( {\overrightarrow {GO} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = \frac{1}{3}\left( { - \overrightarrow {GA} - \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\).
Vậy ta chọn phương án D.
Câu 14:
Cho tứ giác ABCD, O là giao điểm của hai đường chéo. Qua điểm I thuộc đoạn thẳng OB, vẽ đường thẳng song song với đường chéo AC, cắt các cạnh AB, BC và các tia DA, DC theo thứ tự tại các điểm M, N, P, Q.
a) Chứng minh \(\frac{{IM}}{{OA}} = \frac{{IB}}{{OB}}\) và \(\frac{{IM}}{{IP}} = \frac{{IB}}{{ID}}.\frac{{OD}}{{OB}}\).
b) Chứng minh \(\frac{{IM}}{{IP}} = \frac{{IN}}{{IQ}}\).
 Xem đáp án
Xem đáp án
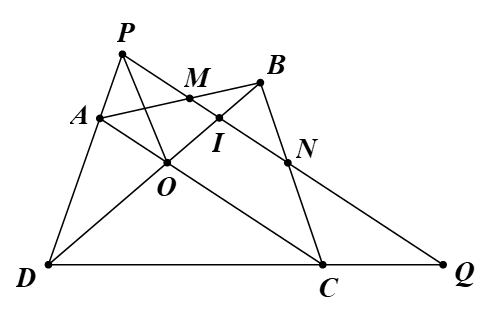
a) Tam giác OAB có IM // OA nên áp dụng định lí Thales, ta được: \(\frac{{IM}}{{OA}} = \frac{{IB}}{{OB}}\) (1)
Tam giác DPI có OA // IP nên áp dụng định lí Thales, ta được \(\frac{{OA}}{{IP}} = \frac{{OD}}{{ID}}\) (2)
Từ (1), (2), suy ra \(\frac{{IM}}{{OA}}.\frac{{OA}}{{IP}} = \frac{{IB}}{{OB}}.\frac{{OD}}{{ID}}\).
\( \Leftrightarrow \frac{{IM}}{{IP}} = \frac{{IB}}{{ID}}.\frac{{OD}}{{OB}}\).
Vậy ta có điều phải chứng minh.
b) Tam giác OBC có IN // OC nên áp dụng định lí Thales, ta được \(\frac{{IN}}{{OC}} = \frac{{IB}}{{OB}}\) (3)
Tam giác DQI có OC // IQ nên áp dụng định lí Thales, ta được \(\frac{{OC}}{{IQ}} = \frac{{OD}}{{ID}}\) (4)
Từ (3), (4), suy ra \(\frac{{IN}}{{OC}}.\frac{{OC}}{{IQ}} = \frac{{IB}}{{OB}}.\frac{{OD}}{{ID}}\).
\( \Leftrightarrow \frac{{IN}}{{IQ}} = \frac{{IB}}{{ID}}.\frac{{OD}}{{OB}} = \frac{{IM}}{{IP}}\).
Vậy ta có điều phải chứng minh.
Câu 15:
Cho đường thẳng (d): y = 2x + 3 và đường thẳng (d’): y = (m + 1)x + 5 (m là tham số, m ≠ –1).
a) Vẽ đường thẳng (d) trên hệ trục tọa độ Oxy.
b) Tìm m để đường thẳng (d) song song với đường thẳng (d’).
c) Tìm m để hai đường thẳng (d) và (d’) cắt nhau tại điểm A nằm bên trái trục tung.
 Xem đáp án
Xem đáp án
a) Bảng giá trị:
|
x |
–1 |
0 |
1 |
|
y |
1 |
3 |
5 |
Đồ thị:
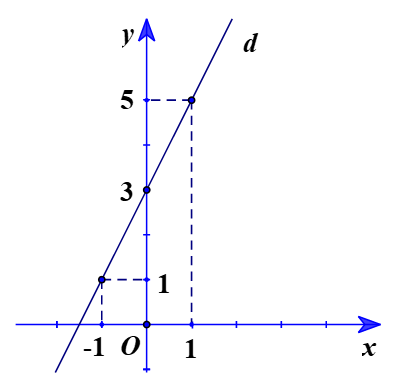
b) Ta có d // d’.
Suy ra \[\left\{ \begin{array}{l}m + 1 = 2\\5 \ne 3\end{array} \right.\]
Do đó m = 1.
Vậy m = 1 thỏa mãn yêu cầu bài toán.
c) Phương trình hoành độ giao điểm của (d) và (d’): (m + 1)x + 5 = 2x + 3.
⇔ (m – 1)x = –2 (điều kiện: m ≠ 1).
\( \Leftrightarrow x = \frac{{ - 2}}{{m - 1}}\).
Suy ra tọa độ \(A\left( {\frac{{ - 2}}{{m - 1}};{y_A}} \right)\).
Ta có hai đường thẳng (d) và (d’) cắt nhau tại điểm A nằm bên trái trục tung.
⇒ x < 0.
\( \Rightarrow \frac{{ - 2}}{{m - 1}} < 0\).
⇒ m – 1 > 0.
⇒ m > 1.
So với điều kiện m ≠ 1, ta nhận m > 1.
Vậy m > 1 thỏa mãn yêu cầu bài toán.
Câu 16:
Cho đường tròn (O) và điểm A bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). AC cắt đường tròn (O) tại D (D khác C).
a) Chứng minh rằng BD vuông góc AC và AB2 = AD.AC.
b) Từ C vẽ dây CE // OA. BE cắt OA tại H. Chứng minh rằng H là trung điểm của BE và AE là tiếp tuyến.
c) Chứng minh rằng \(\widehat {OCH} = \widehat {OAC}\).
d) Tia OA cắt đường tròn tại F. Chứng minh rằng FA.CH = HF.CA.
 Xem đáp án
Xem đáp án
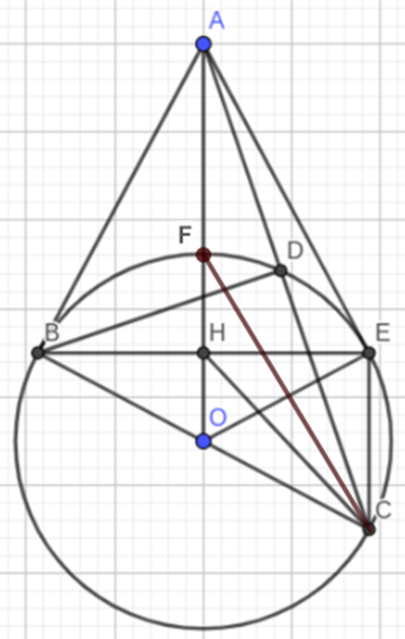
a) Vì D thuộc đường tròn (O) và BC là đường kính nên \(\widehat {BDC} = 90^\circ \).
Suy ra BD ⊥ AC.
Ta có AB là tiếp tuyến của (O), với B là tiếp điểm.
Suy ra \(\widehat {ABC} = 90^\circ \).
Tam giác ABC vuông tại B có BD là đường cao: AB2 = AD.AC (Hệ thức lượng trong tam giác vuông).
Vậy BD vuông góc AC và AB2 = AD.AC.
b) Xét tam giác BEC có O là trung điểm BC (do BC là đường kính của (O)) và OH // CE (giả thiết).
Suy ra OH là đường trung bình của tam giác BEC.
Vậy H là trung điểm của BE.
Vì E thuộc đường tròn (O) và BC là đường kính nên \(\widehat {BEC} = 90^\circ \).
Suy ra BE ⊥ CE.
Mà CE // OH (giả thiết).
Do đó OH ⊥ BE hay AH ⊥ BE.
Tam giác ABE có AH vừa là đường trung tuyến, vừa là đường cao.
Suy ra tam giác ABE cân tại A.
Do đó AB = AE.
Xét ∆ABO và ∆AEO, có:
AO chung;
AB = AE (chứng minh trên);
OB = OE (= R).
Do đó ∆ABO = ∆AEO (c.c.c).
Suy ra \(\widehat {AEO} = \widehat {ABO} = 90^\circ \) (cặp góc tương ứng).
Vậy AE là tiếp tuyến của (O).
c) Tam giác OBA vuông tại B có BH là đường cao: OB2 = OH.OA (Hệ thức lượng trong tam giác vuông).
Suy ra OC2 = OH.OA.
Xét ∆OHC và ∆OCA, có:
\(\frac{{OH}}{{OC}} = \frac{{OC}}{{OA}}\) (OC2 = OH.OA);
\(\widehat {COH}\) chung.
Do đó (c.g.c).
Vậy \(\widehat {OCH} = \widehat {OAC}\) (cặp góc tương ứng).
d) Ta có \(\widehat {OCF} = \widehat {FCE}\,\,\left( { = \widehat {OFC}} \right)\).
Lại có \(\widehat {OCH} = \widehat {ACE}\,\,\left( { = \widehat {OAC}} \right)\).
Suy ra \(\widehat {HCF} = \widehat {FCA}\).
Khi đó CF là tia phân giác của \(\widehat {HCA}\).
Áp dụng tính chất đường phân giác cho tam giác HCA, ta được: \(\frac{{HF}}{{FA}} = \frac{{HC}}{{CA}}\).
Vậy FA.CH = HF.CA (điều phải chứng minh).
Câu 17:
Cho đường tròn (O) và điểm A ngoài (O). Qua A kẻ các tiếp tuyến AB, AC với (O) trong đó B, C là các tiếp điểm. Lấy M là điểm thuộc cung nhỏ BC. Tiếp tuyến qua M với (O) cắt AB, AC lần lượt tại D và E. Chứng minh:
a) Chu vi tam giác ADE bằng 2AB.
b) \(\widehat {DOE} = \frac{1}{2}\widehat {BOC}\).
 Xem đáp án
Xem đáp án
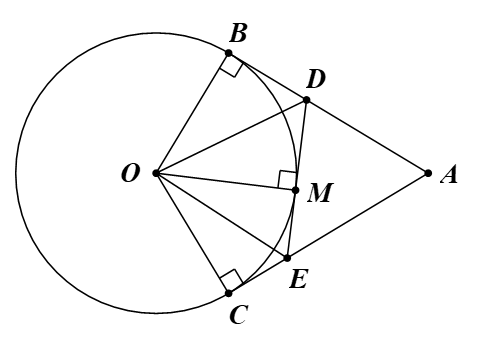
a) Ta có BD, MD là hai tiếp tuyến của (O).
Suy ra DB = DM (tính chất hai tiếp tuyến cắt nhau).
Chứng minh tương tự, ta được ME = CE và AB = AC.
Ta có chu vi tam giác ADE là: AD + DE + EA = AD + DM + ME + AE
= AD + DB + CE + AE = AB + AC = 2AB.
Vậy ta có điều phải chứng minh.
b) Ta có , MD là hai tiếp tuyến của (O).
Suy ra OD là tia phân giác của \(\widehat {BOM}\) (tính chất hai tiếp tuyến cắt nhau).
Do đó \(\widehat {DOM} = \frac{1}{2}\widehat {BOM}\).
Chứng minh tương tự, ta được \(\widehat {MOE} = \frac{1}{2}\widehat {MOC}\).
Ta có \(\widehat {DOE} = \widehat {DOM} + \widehat {MOE} = \frac{1}{2}\widehat {BOM} + \frac{1}{2}\widehat {MOC} = \frac{1}{2}\left( {\widehat {BOM} + \widehat {MOC}} \right) = \frac{1}{2}\widehat {BOC}\).
Vậy ta có điều phải chứng minh.
Câu 18:
Cho đường thẳng d cắt đường tròn (O; R) tại hai điểm C, D. M là một điểm thuộc d và nằm ngoài (O; R) (MC < MD). Vẽ hai tiếp tuyến MA, MB với (O; R). H là trung điểm của CD. Đường thẳng AB cắt OH tại E. Chứng minh ED là tiếp tuyến của (O; R).
 Xem đáp án
Xem đáp án
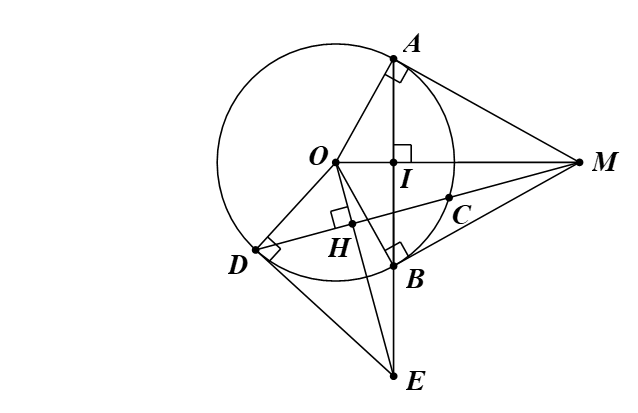
Ta có MA, MB là tiếp tuyến của (O).
Suy ra MA = MB và MO là tia phân giác của \[\widehat {AMB}\] (tính chất hai tiếp tuyến cắt nhau).
Khi đó tam giác AMB cân tại A có MO là đường phân giác.
Vì vậy MO cũng là đường cao của tam giác AMB.
Suy ra MO ⊥ AB tại I.
Ta có H là trung điểm CD (giả thiết).
Suy ra OH ⊥ CD tại H (quan hệ đường kính và dây cung).
Xét ∆OHM và ∆OIE, có:
\(\widehat {OHM} = \widehat {OIE} = 90^\circ \);
\(\widehat {MOE}\) chung.
Do đó (g.g).
Suy ra \(\frac{{OH}}{{OI}} = \frac{{OM}}{{OE}}\).
Vì vậy OH.OE = OM.OI.
Tam giác AOM vuông tại A (vì AM là tiếp tuyến của (O)) có AI là đường cao:
OA2 = OI.OM (Hệ thức lượng trong tam giác vuông).
Suy ra OD2 = OH.OE.
Xét ∆ODH và ∆OED, có:
\(\widehat {DOE}\) chung;
\(\frac{{OD}}{{OE}} = \frac{{OH}}{{OD}}\) (OD2 = OH.OE).
Do đó (c.g.c).
Suy ra \(\widehat {ODE} = \widehat {OHD} = 90^\circ \) (cặp góc tương ứng).
Vậy ED là tiếp tuyến của (O; R).
Câu 19:
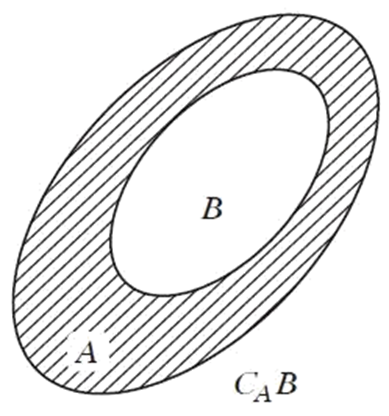
Kí hiệu A \ B là gì?
 Xem đáp án
Xem đáp án
⦁ Tập hợp C gồm các phần tử thuộc A nhưng không thuộc B được gọi là hiệu của A và B.
Kí hiệu \(x \in A\backslash B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \notin B\end{array} \right.\)
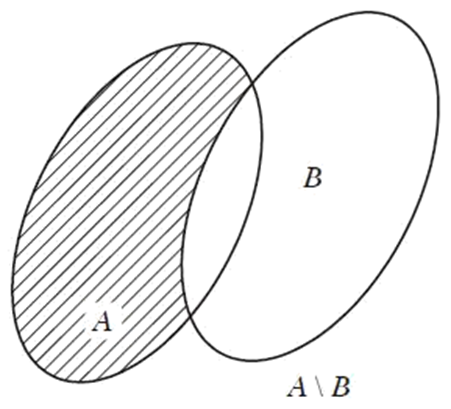
⦁ Khi B ⊂ A thì A \ B gọi là phần bù của B trong A, kí hiệu CAB.
Câu 20:
Lấy điểm A trên (O; R), vẽ tiếp tuyến Ax. Trên Ax lấy điểm B. Trên (O; R) lấy điểm C sao cho BC = AB.
a) Chứng minh CB là tiếp tuyến của (O).
b) Vẽ đường kính AD của (O), kẻ CK vuông góc với AD. Chứng minh rằng CD // OB và BC.CD = CK.OB.
c) Lấy điểm M trên cung nhỏ AC của (O). Vẽ tiếp tuyến tại M cắt AB, BC lần lượt tại E, F. Vẽ đường tròn tâm I nội tiếp ∆BEF. Chứng minh .
 Xem đáp án
Xem đáp án
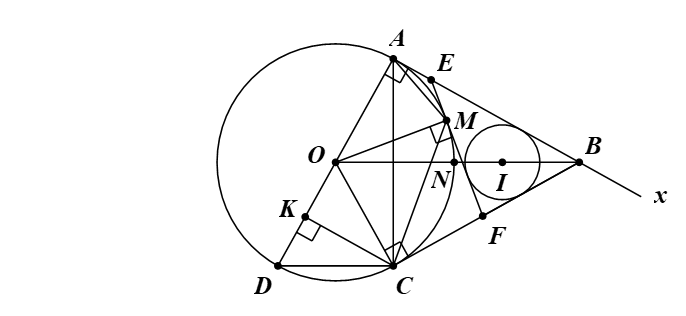
a) Ta có \(\widehat {OAB} = 90^\circ \) (do AB là tiếp tuyến của (O)).
Xét ∆ABO và ∆CBO, có:
OB chung;
AB = BC (giả thiết);
OA = OC (= R).
Do đó ∆ABO = ∆CBO (c.c.c).
Suy ra \(\widehat {OCB} = \widehat {OAB} = 90^\circ \).
Vậy CB là tiếp tuyến của (O).
b) Gọi N là giao điểm của OB và (O).
Ta có \(\widehat {AOB} = \widehat {BOC}\) (∆ABO = ∆CBO).
Suy ra sđ = sđ.
Lại có \(\widehat {AOB}\) = sđ và \(\widehat {ODC} = \frac{1}{2}\)sđ = sđ.
Do đó \(\widehat {AOB} = \widehat {ODC}\).
Mà hai góc này ở vị trí đồng vị.
Vậy CD // OB.
Xét ∆OBC và ∆DCK, có:
\(\widehat {BOC} = \widehat {KDC}\,\,\left( { = \widehat {OCD}} \right)\);
\(\widehat {OCB} = \widehat {CKD} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{BC}}{{CK}} = \frac{{OB}}{{CD}}\).
Vậy BC.CD = CK.OB.
c) Ta có I là tâm đường tròn nội tiếp tam giác BEF.
Suy ra EI là tia phân giác của \(\widehat {BEF}\).
Do đó \(\widehat {IEF} = \frac{1}{2}\widehat {BEF}\) (1)
Tứ giác EAOM, có: \(\widehat {EAO} = \widehat {EMO} = 90^\circ \) (AE, ME là tiếp tuyến của (O)).
Suy ra \(\widehat {EAO} + \widehat {EMO} = 180^\circ \).
Do đó tứ giác EAOM nội tiếp đường tròn đường kính OE.
Vì vậy \(\widehat {BEF} = \widehat {AOM}\) (2)
Đường tròn (O; R), có: \(\widehat {AOM}\) là góc ở tâm chắn và \(\widehat {MCA}\) là góc nội tiếp chắn .
Suy ra \(\widehat {AOM} = 2\widehat {MCA}\) (3)
Từ (1), (2), (3), suy ra \(\widehat {IEF} = \widehat {MCA}\).
Chứng minh tương tự, ta được: \(\widehat {IFE} = \widehat {MAC}\).
Xét ∆MAC và ∆IFE, có:
\(\widehat {IEF} = \widehat {MCA}\) (chứng minh trên);
\(\widehat {IFE} = \widehat {MAC}\) (chứng minh trên).
Vậy (g.g).
Câu 21:
Trong các số thập phân 86,42; 86,422; 686,42; 86,642. Số thập phân lớn nhất là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có 86 < 686.
Do đó số có phần nguyên là 686 là số lớn nhất.
Vậy ta chọn phương án C.
Câu 22:
Tìm m để parabol (P): y = x2 – 2mx + m + 3 có đỉnh nằm trên đường thẳng (d): y = x + 2.
 Xem đáp án
Xem đáp án
Cho S là đỉnh của parabol, khi đó:
• \({x_S} = - \frac{b}{{2a}} = - \frac{{ - 2m}}{{2.1}} = m\).
• \({y_S} = - \frac{\Delta }{{4a}} = - \frac{{{{\left( { - 2m} \right)}^2} - 4\left( {m + 3} \right)}}{4} = - \frac{{4{m^2} - 4m - 12}}{4} = - {m^2} + m + 3\).
Do đó \(S\left( {m; - {m^2} + m + 3} \right)\).
Để S nằm trên (d) thì –m2 + m + 3 = m + 2
Û m2 = 1 Û m = ± 1.
Vậy m = ± 1.
Câu 23:
Tìm m để các hàm số sau có tập xác định là ℝ (hay luôn xác định trên ℝ):
a) \(y = f\left( x \right) = \frac{{3x + 1}}{{{x^2} + 2\left( {m - 1} \right)x + {m^2} + 3m + 5}}\).
b) \(y = f\left( x \right) = \sqrt {{x^2} + 2\left( {m - 1} \right)x + {m^2} + m - 6} \).
c) \(y = f\left( x \right) = \frac{{3x + 5}}{{\sqrt {{x^2} - 2\left( {m + 3} \right)x + m + 9} }}\).
 Xem đáp án
Xem đáp án
a) Hàm số đã cho có tập xác định là ℝ.
⇔ x2 + 2(m – 1)x + m2 + 3m + 5 ≠ 0, ∀x ∈ ℝ.
⇔ ∆’ = (m – 1)2 – (m2 + 3m + 5) < 0.
⇔ m2 – 2m + 1 – m2 – 3m – 5 < 0.
⇔ –5m – 4 < 0.
\( \Leftrightarrow m > \frac{{ - 4}}{5}\).
Vậy \(m > \frac{{ - 4}}{5}\) thỏa mãn yêu cầu bài toán.
b) Hàm số đã cho có tập xác định là ℝ.
⇔ x2 + 2(m – 1)x + m2 + m – 6 ≥ 0, ∀x ∈ ℝ.
⇔ ∆’ = (m – 1)2 – (m2 + m – 6) ≤ 0.
⇔ m2 – 2m + 1 – m2 – m + 6 ≤ 0.
⇔ –3m + 7 ≤ 0.
\( \Leftrightarrow m \ge \frac{7}{3}\).
Vậy \(m \ge \frac{7}{3}\) thỏa mãn yêu cầu bài toán.
c) Hàm số đã cho có tập xác định là ℝ.
⇔ x2 – 2(m + 3)x + m + 9 > 0, ∀x ∈ ℝ.
⇔ ∆’ = (m + 3)2 – (m + 9) < 0.
⇔ m2 + 6m + 9 – m – 9 < 0.
⇔ m2 + 5m < 0.
⇔ –5 < m < 0.
Vậy –5 < m < 0 thỏa mãn yêu cầu bài toán.
Câu 24:
Tìm một số tự nhiên có 3 chữ số, biết rằng khi viết thêm chữ số 2 vào bên phải số đó thì nó tăng 4106 đơn vị.
 Xem đáp án
Xem đáp án
Gọi số cần tìm là \(\overline {abc} \) (a, b, c ∈ ℕ, 0 ≤ a, b, c ≤ 9 và a ≠ 0).
Theo đề, ta có khi viết thêm chữ số 2 vào bên phải số đó thì nó tăng 4106 đơn vị.
Nghĩa là, \(\overline {abc2} = \overline {abc} + 4106\).
\( \Rightarrow \overline {abc} \times 10 + 2 = \overline {abc} + 4106\).
\( \Rightarrow \overline {abc} \times 9 = 4104\).
\[ \Rightarrow \overline {abc} = 4104:9 = 456\].
Vậy số cần tìm là 456.
Câu 25:
Cho phương trình x2 + 2(m – 1)x – (m + 1) = 0. Tìm m để phương trình có 2 nghiệm nhỏ hơn 2.
 Xem đáp án
Xem đáp án
Ta có x2 + 2(m – 1)x – (m + 1) = 0 (1)
∆’ = (m – 1)2 + (m + 1) = m2 – 2m + 1 + m + 1 = m2 – m + 2.
\( = {\left( {m - \frac{1}{2}} \right)^2} + \frac{7}{4} \ge \frac{7}{4} > 0,\,\,\forall m \in \mathbb{R}\).
Vậy phương trình (1) luôn có hai nghiệm phân biệt với mọi m.
Theo Viet: \(S = {x_1} + {x_2} = - \frac{b}{a} = - 2\left( {m - 1} \right)\).
\(P = {x_1}{x_2} = \frac{c}{a} = - m - 1\).
Từ giả thiết, ta có x1 – 2 < 0 và x2 – 2 < 0.
\( \Leftrightarrow \left\{ \begin{array}{l}\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) > 0\\{x_1} + {x_2} < 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 > 0\\ - 2\left( {m - 1} \right) < 4\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - m - 1 + 4.\left( {m - 1} \right) + 4 > 0\\m - 1 > - 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}3m - 1 > 0\\m > - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > \frac{1}{3}\\m > - 1\end{array} \right.\)
\( \Leftrightarrow m > \frac{1}{3}\).
Vậy \(m > \frac{1}{3}\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 26:
Tìm x, biết: \(x \times 30\% + x \times \frac{1}{4} + 89 = 100\).
 Xem đáp án
Xem đáp án
Ta có \(x \times 30\% + x \times \frac{1}{4} + 89 = 100\).
\(x \times \frac{3}{{10}} + x \times \frac{1}{4} = 100 - 89\).
\(x \times \left( {\frac{3}{{10}} + \frac{1}{4}} \right) = 11\).
\(x \times \frac{{11}}{{20}} = 11\).
\(x = 11:\frac{{11}}{{20}}\).
x = 20.
Vậy x = 20.
Câu 27:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với đáy và góc tạo bởi SB với đáy (ABC) bằng 60°. Tính thể tích khối chóp S.ABC tính theo a.
 Xem đáp án
Xem đáp án

Ta có A, B lần lượt là hình chiếu vuông góc của S, B lên (ABC).
Suy ra AB là hình chiếu vuông góc của SB lên (ABC).
Do đó góc tạo bởi SB với đáy là \(\left( {SB,AB} \right) = \widehat {SBA} = 60^\circ \).
Tam giác SAB vuông tại A: \(SA = AB.\tan \widehat {SBA} = a.\tan 60^\circ = a\sqrt 3 \).
Gọi I là trung điểm BC. Suy ra \(BI = \frac{{BC}}{2} = \frac{a}{2}\).
Tam giác ABC đều có AI là đường trung tuyến.
Suy ra AI cũng là đường cao của tam giác ABC.
Do đó AI ⊥ BC.
Tam giác ABI vuông tại I: \(AI = \sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\).
Vậy thể tích khối chóp S.ABC là: \[V = \frac{1}{3}SA.{S_{\Delta ABC}} = \frac{1}{3}.a\sqrt 3 .\frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^3}}}{4}\].
Câu 28:
Cho hình vuông ABCD có AC cắt BD tại O. Gọi E và F theo thứ tự là các điểm đối xứng với O qua AD và BC.
a) Chứng minh rằng các tứ giác AODE, BOCF là hình vuông.
b) Nối CE cắt DF tại I. Chứng minh rằng OI ⊥ CD.
c) Biết diện tích của hình lục giác ABFCDE bằng 6. Tính độ dài cạnh của hình vuông ABCD.
d) Lấy K là một điểm bất kì trên cạnh BC. Gọi G là trọng tâm của ∆AIK. Chứng minh rằng điểm G thuộc một đường thẳng cố định khi K di chuyển trên cạnh BC.
 Xem đáp án
Xem đáp án
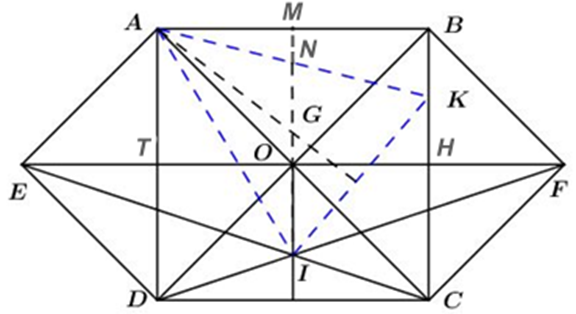
a) Gọi T là giao điểm của AD và EO; H là giao điểm của BC và OF.
Vì E là điểm đối xứng của O qua AD nên AD là đường trung trực của đoạn OE.
Khi đó AO = AE.
Vì vậy tam giác OAE cân tại A.
Tam giác OAE cân tại A có AT là đường trung trực.
Suy ra AT cũng là đường phân giác của tam giác OAE.
Do đó \(\widehat {EAT} = \widehat {TAO} = 45^\circ \) (do ABCD là hình vuông).
Vì vậy \(\widehat {EAO} = \widehat {EAT} + \widehat {TAO} = 90^\circ \).
Chứng minh tương tự, ta được: \(\widehat {EDO} = 90^\circ \).
Xét tứ giác AODE, có: \(\widehat {EAO} = \widehat {EDO} = 90^\circ \) (chứng minh trên) và \(\widehat {AOD} = 90^\circ \) (ABCD là hình vuông).
Suy ra tứ giác AODE là hình chữ nhật.
Mà OA = OD (ABCD là hình vuông tâm O).
Vậy tứ giác AODE là hình vuông.
Chứng minh tương tự, ta được: tứ giác BOCF là hình vuông.
b) Ta có E và F theo thứ tự là các điểm đối xứng với O qua AD và BC.
Suy ra OE ⊥ AD và OF ⊥ BC.
Mà AD // BC (ABCD là hình vuông).
Do đó OE ⊥ BC.
Mà OF ⊥ BC (chứng minh trên).
Vì vậy ba điểm E, O, F thẳng hàng.
Xét ∆ECF và ∆FDE, có:
EF là cạnh chung;
FC = DE (OC = OD);
\(\widehat {CFE} = \widehat {DEF} = 45^\circ \).
Do đó ∆ECF = ∆FDE (c.g.c).
Suy ra \(\widehat {FEC} = \widehat {DFE}\) (cặp góc tương ứng).
Vì vậy tam giác EIF cân tại I.
Mà O là trung điểm của EF (OE = AD; OF = BC và AD = BC).
Suy ra OI là vừa là đường trung tuyến, vừa là đường cao của tam giác EIF.
Do đó OI ⊥ EF (1)
Ta có EF ⊥ AD (chứng minh trên) và AD ⊥ BC (ABCD là hình vuông).
Suy ra EF // CD (2)
Từ (1), (2), ta thu được OI ⊥ CD.
c) Ta có AODE là hình vuông (câu a).
Suy ra SAOD = SAED (tính chất hình vuông) (3)
Chứng minh tương tự, ta được: SBFC = SBOC (4)
Xét ∆AOD và ∆AOB, có:
AB = AD (ABCD là hình vuông);
AO là cạnh chung;
OB = OD (O là trung điểm BD).
Do đó ∆AOD = ∆AOB (c.c.c).
Suy ra SAOD = SAOB (5)
Chứng minh tương tự, ta được SDOC = SBOC và SAOB = SBOC (6)
Từ (3), (4), (5), (6), suy ra SAOD = SAED = SBFC = SBOC = SAOB = SDOC.
Theo đề ta có SABFCDE = 6.
Suy ra 6SABO = 6.
Do đó SABO = 1.
Vì vậy SABCD = SABO + SAOD + SDOC + SBOC = 4SABO = 4.
Suy ra AB2 = 4.
Vậy AD = CD = BC = AB = 2.
d) Gọi M là giao điểm của OI và AB; N là giao điểm của IM và AK.
Ta có OE = OF (O là trung điểm của EF).
Suy ra 2OT = 2OH.
Vì vậy OT = OH.
Vì OI ⊥ CD và CD // AB nên OI ⊥ AB hay OM ⊥ AB.
Mà O là trung điểm của HT (OT = OH).
Suy ra M là trung điểm của AB.
Tam giác ABK, có: MA = MB (M là trung điểm của AB) và MN // BK (cùng vuông góc với AB).
Do đó MN là đường trung bình của tam giác ABK.
Suy ra N là trung điểm AK.
Vì vậy IN là đường trung tuyến của tam giác AIK.
Mà G là trọng tâm của tam giác AIK.
Khi đó G ∈ IN hay G ∈ IM.
Mà I, M cố định.
Vậy điểm G thuộc một đường thẳng cố định IM khi K di chuyển trên cạnh BC.
Câu 29:
Mua 5 kg đường phải trả 85 000 đồng. Hỏi mua 3,5 kg đường cùng loại phải trả ít hơn bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Mua 1 kg đường phải trả số tiền là:
85 000 : 5 = 17 000 (đồng)
Mua 3,5 kg đường phải trả số tiền là:
17 000 × 3,5 = 59 500 (đồng)
Mua 3,5 kg đường phải trả ít hơn mua 5kg đường cùng loại số tiền là:
85 000 – 59 500 = 25 500 (đồng)
Đáp số: 25 500 đồng.
Câu 30:
Tính \(\int\limits_0^\pi {\sqrt {1 + \sin 2x} dx} \).
 Xem đáp án
Xem đáp án
Ta có \(\int\limits_0^\pi {\sqrt {1 + \sin 2x} dx} = \int\limits_0^\pi {\sqrt {{{\sin }^2}x + {{\cos }^2}x + 2\sin x.\cos x} dx} \).
\( = \int\limits_0^\pi {\sqrt {{{\left( {\sin x + \cos x} \right)}^2}} dx} = \int\limits_0^\pi {\left| {\sin x + \cos x} \right|dx} \).
\[ = \int\limits_0^\pi {\left| {\sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right)} \right|dx} = \sqrt 2 \int\limits_0^{\frac{{3\pi }}{4}} {\cos \left( {x - \frac{\pi }{4}} \right)dx} - \sqrt 2 \int\limits_{\frac{{3\pi }}{4}}^\pi {\cos \left( {x - \frac{\pi }{4}} \right)dx} \].
\[ = \sqrt 2 \sin \left. {\left( {x - \frac{\pi }{4}} \right)} \right|_0^{\frac{{3\pi }}{4}} - \sqrt 2 \sin \left. {\left( {x - \frac{\pi }{4}} \right)} \right|_{\frac{{3\pi }}{4}}^\pi = \sqrt 2 + 1 - \left( {1 - \sqrt 2 } \right) = 2\sqrt 2 \].
Vậy \(\int\limits_0^\pi {\sqrt {1 + \sin 2x} dx} = 2\sqrt 2 \).
Câu 31:
Chứng minh rằng với mọi số thực b, c, ta có: (b + c)2 ≤ 2(b2 + c2).
 Xem đáp án
Xem đáp án
Ta có (b + c)2 ≤ 2(b2 + c2).
⇔ b2 + 2bc + c2 ≤ 2b2 + 2c2.
⇔ b2 – 2bc + c2 ≥ 0.
⇔ (b – c)2 ≥ 0, luôn đúng với mọi b, c ∈ ℝ.
Dấu “=” xảy ra ⇔ b = c.
Vậy ta có điều phải chứng minh.
Câu 32:
Cho a ≠ b ≠ c thỏa mãn a2(b + c) = b2(c + a) = 2012. Tính M = c2(a + b).
 Xem đáp án
Xem đáp án
Ta có a2(b + c) = b2(c + a).
⇔ a2b – ab2 + a2c – b2c = 0.
⇔ ab(a – b) + c(a2 – b2) = 0.
⇔ ab(a – b) + c(a – b)(a + b) = 0.
⇔ (a – b)(ab + ca + bc) = 0 (vì a ≠ b nên a – b ≠ 0).
⇔ ab + bc + ca = 0.
Lại có a2(b + c) = b2(c + a).
\( \Leftrightarrow \frac{{{a^2}}}{{c + a}} = \frac{{{b^2}}}{{b + c}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{{{a^2}}}{{c + a}} = \frac{{{b^2}}}{{b + c}} = \frac{{{a^2} - {b^2}}}{{c + a - b - c}} = \frac{{\left( {a - b} \right)\left( {a + b} \right)}}{{a - b}} = a + b\) (a ≠ b).
⇒ a2 = (a + b)(a + c).
⇒ a2(b + c) = (a + b)(a + c)(b + c).
⇒ 2012 = (a + b)(ab + ac + bc + c2).
⇒ 2012 = (a + b)c2.
Vậy M = c2(a + b) = 2012.
Câu 33:
Phân tích số 20 ra thừa số nguyên tố.
 Xem đáp án
Xem đáp án
Ta có 20 = 22.5.
Vậy khi phân tích số 20 ra thừa số nguyên tố, ta được kết quả là 22.5.
Câu 34:
Tìm x, biết: \(\left| {{x^2}\left| {x + \frac{3}{4}} \right|} \right| = {x^2}\).
 Xem đáp án
Xem đáp án
Ta có x2 ≥ 0, ∀x ∈ ℝ.
Ta có \(\left| {{x^2}\left| {x + \frac{3}{4}} \right|} \right| = {x^2}\).
\( \Rightarrow {x^2}\left| {x + \frac{3}{4}} \right| = {x^2}\) hoặc \({x^2}\left| {x + \frac{3}{4}} \right| = - {x^2}\).
\( \Rightarrow {x^2}\left( {\left| {x + \frac{3}{4}} \right| - 1} \right) = 0\) hoặc \({x^2}\left( {\left| {x + \frac{3}{4}} \right| + 1} \right) = 0\).
\( \Rightarrow \left[ \begin{array}{l}{x^2} = 0\\\left| {x + \frac{3}{4}} \right| = 1\end{array} \right.\) hoặc \(\left[ \begin{array}{l}{x^2} = 0\\\left| {x + \frac{3}{4}} \right| = - 1\end{array} \right.\) (vô lí).
\( \Rightarrow \left[ \begin{array}{l}x = 0\\x + \frac{3}{4} = 1\\x + \frac{3}{4} = - 1\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = \frac{1}{4}\\x = - \frac{7}{4}\end{array} \right.\)
Vậy \(\left[ \begin{array}{l}x = 0\\x = \frac{1}{4}\\x = - \frac{7}{4}\end{array} \right.\).
Câu 35:
Giải phương trình: (x2 + 2x)2 – 6x2 – 12x + 5 = 0.
 Xem đáp án
Xem đáp án
Ta có (x2 + 2x)2 – 6x2 – 12x + 5 = 0.
⇔ (x2 + 2x)2 – 6(x2 + 2x) + 5 = 0 (1)
Đặt t = x2 + 2x.
Phương trình (1) tương đương với: t2 – 6t + 5 = 0.
⇔ t = 5 hoặc t = 1.
Với t = 5, ta có: x2 + 2x – 5 = 0.
\( \Leftrightarrow x = - 1 \pm \sqrt 6 \).
Với t = 1, ta có: x2 + 2x – 1 = 0.
\( \Leftrightarrow x = - 1 \pm \sqrt 2 \).
Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - 1 \pm \sqrt 6 ; - 1 \pm \sqrt 2 } \right\}\).
Câu 36:
Mức lương của công nhân tăng 20%, giá mua hàng giảm 20%. Hỏi với mức lương này thì lượng hàng mới sẽ mua được nhiều hơn lượng hàng cũ bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Giả sử mức lương cũ là 100%. Suy ra mức lương mới là 120% mức lương cũ.
Giả sử giá hàng cũ là 100%. Suy ra giá hàng mới là 80% giá hàng cũ.
Tỉ số phần trăm giữa lượng hàng mới và hàng cũ là: \(\frac{{120}}{{80}} = 1,5 = 150\% \).
Vậy lượng hàng mới sẽ mua được nhiều hơn lượng hàng cũ là: 150% – 100% = 50%.
Câu 37:
Cho tam giác ABC vuông tại B, đường trung tuyến BM, đường cao BH. Lấy E đối xứng với B qua M.
a) Chứng minh tứ giác ABCE là hình chữ nhật.
b) Qua E kẻ đường thẳng song song với AC cắt BC tại D, cắt BH tại I. Chứng minh tứ giác ACDE là hình bình hành.
c) Chứng minh EI // AM.
d) Chứng minh tứ giác AIEC là hình thang cân.
e) Tam giác ABC cần thêm điều kiện gì để ABCE là hình vuông?
 Xem đáp án
Xem đáp án
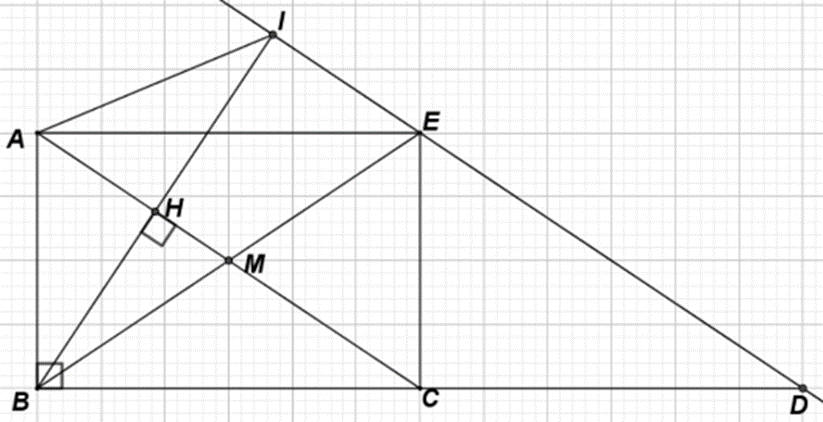
a) Ta có M là trung điểm AC (giả thiết) và M là trung điểm BE (E là điểm đối xứng với B qua M).
Suy ra tứ giác ABCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Do đó tứ giác ABCE là hình bình hành.
Mà \[\widehat {ABC} = 90^\circ \].
Vậy tứ giác ABCE là hình chữ nhật.
b) Ta có AE // CD (do tứ giác ABCE là hình chữ nhật) và DE // AC (giả thiết).
Vậy tứ giác tứ giác ACDE là hình bình hành.
c) Vì M thuộc AC, I thuộc DE và AC // DE (giả thiết).
Vậy EI // AM.
d) Ta có HM // IE (giả thiết) và M là trung điểm của BE (chứng minh trên).
Suy ra HM là đường trung bình của tam giác BIE.
Do đó H là trung điểm của BI.
Mà BI ⊥ AH (giả thiết).
Vì vậy AH là đường trung trực của đoạn BI.
Suy ra AB = AI.
Mà AB = CE (ABCE là hình chữ nhật).
Khi đó AI = CE.
Tứ giác AIEC, có: AI = CE (chứng minh trên) và IE // AC (giả thiết).
Vậy tứ giác AIEC là hình thang cân.
e) Ta có tứ giác ABCE là hình chữ nhật (kết quả câu a).
Để tứ giác ABCE là hình vuông thì cần thêm điều kiện AB = BC.
Vậy tam giác ABC vuông cân tại B thì tứ giác ABCE là hình vuông.
Câu 38:
Có 8 cái bút khác nhau và 9 quyển vở khác nhau được gói trong 17 hộp. Một học sinh được chọn bất kì hai hộp. Xác suất để học sinh đó chọn được một cặp bút và vở là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{17}^2 = 136\).
Gọi biến cố A: “Chọn được một cặp bút và vở”.
Khi đó \(n\left( A \right) = C_8^1.C_9^1 = 72\).
Vậy xác suất để học sinh đó chọn được một cặp bút và vở là:
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{72}}{{136}} = \frac{9}{{17}}\).
Do đó ta chọn phương án B.
Câu 39:
Cho hình thoi ABCD, có O là giao điểm của hai đường chéo AC và BD. Lấy điểm M, N lần lượt là trung điểm của cạnh AD, CD.
a) Nêu nhận xét về quan hệ bằng nhau của \(\widehat {ABD}\) và \(\widehat {ADB}\). Vì sao?
b) Tứ giác AMNC là hình gì? Vì sao?
c) Chứng minh tứ giác OMDN là hình thoi.
d) Gọi E là giao điểm của đường thẳng BM với đường thẳng CD. Tính số đo \(\widehat {AED}\), biết \(\widehat {BAD} = 130^\circ \).
 Xem đáp án
Xem đáp án
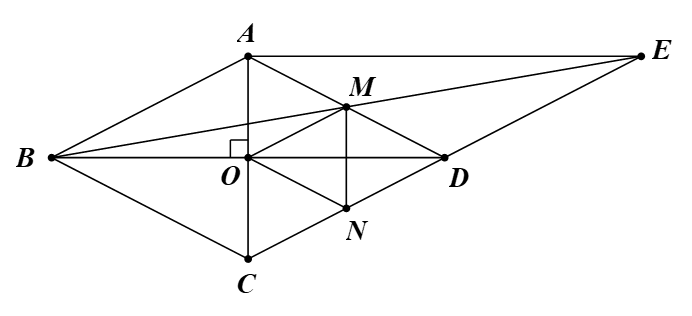
a) Ta có ABCD là hình thoi (giả thiết).
Suy ra AB = AD.
Do đó tam giác ABD cân tại A.
Vậy \(\widehat {ABD} = \widehat {ADB}\).
b) Chứng minh tương tự câu a, ta được \(\widehat {DAC} = \widehat {DCA}\) (1)
Tam giác ACD có M, N lần lượt là trung điểm của AD, CD.
Suy ra MN là đường trung bình của tam giác ACD.
Do đó MN // AC (2)
Từ (1), (2) ta thu được tứ giác AMNC là hình thang cân.
c) Vì ABCD là hình thoi tâm O nên AC ⊥ BD tại O.
Tam giác AOD vuông tại O có OM là đường trung tuyến.
Suy ra OM = MD (3)
Chứng minh tương tự, ta được ON = ND (4)
Ta có M, N lần lượt là trung điểm của AD, CD.
Suy ra AD = 2MD và CD = 2ND.
Vì ABCD là hình thoi nên AD = CD.
Suy ra 2MD = 2ND hay MD = ND (5)
Từ (3), (4), (5), suy ra OM = MD = ND = ON.
Vậy tứ giác OMDN là hình thoi.
d) Xét ∆AMB và ∆DME, có:
AM = MD (M là trung điểm AD);
\(\widehat {AMB} = \widehat {DME}\) (đối đỉnh);
\(\widehat {ADE} = \widehat {BAD}\) (AB // CE; cặp góc so le trong).
Do đó ∆AMB = ∆DME (g.c.g).
Suy ra AB = DE (cặp cạnh tương ứng).
Mà AB // CE (ABCD là hình thoi).
Vì vậy tứ giác ABDE là hình bình hành.
Vậy \(\widehat {AED} = \widehat {ABD} = \frac{{180^\circ - \widehat {BAD}}}{2} = 25^\circ \).
Câu 40:
Một lớp học có 30 học sinh gồm cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được 2 nam và 1 nữ là \(\frac{{12}}{{29}}\). Tính số học sinh nữ của lớp.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi biến cố A: “Chọn 2 học sinh nam và 1 học sinh nữ”.
Ta có số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^3\).
Gọi x là số học sinh nữ của lớp (x ∈ ℕ*, x < 30).
Suy ra số học sinh nam của lớp là: 30 – x.
Chọn 2 học sinh nam trong 30 – x học sinh nam thì có \(C_{30 - x}^2\) cách.
Chọn 1 học sinh nữ trong x học sinh nữ thì có \(C_x^1\) cách.
Do đó ta có \(n\left( A \right) = C_{30 - x}^2.C_x^1\).
Theo đề, ta có \(P\left( A \right) = \frac{{12}}{{29}}\).
\( \Leftrightarrow \frac{{C_{30 - x}^2.C_x^1}}{{C_{30}^3}} = \frac{{12}}{{29}}\).
Thay x ở các đáp án vào hệ thức trên, ta thấy x = 14 thỏa mãn.
Vậy lớp đó có 14 học sinh nữ.
Do đó ta chọn phương án C.
Câu 41:
Một lớp học có 30 học sinh gồm cả nam và nữ. Chọn ngẫu nhiên 3 học sinh để tham gia hoạt động của Đoàn trường. Xác suất chọn được 2 nữ và 1 nam là \(\frac{{52}}{{145}}\). Tính số học sinh nữ của lớp.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi biến cố A: “Chọn 1 học sinh nam và 2 học sinh nữ”.
Ta có số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{30}^3\).
Gọi x là số học sinh nữ của lớp (x ∈ ℕ*, x < 30).
Suy ra số học sinh nam của lớp là: 30 – x.
Chọn 1 học sinh nam trong 30 – x học sinh nam thì có \(C_{30 - x}^1\) cách.
Chọn 2 học sinh nữ trong x học sinh nữ thì có \(C_x^2\) cách.
Do đó ta có \(n\left( A \right) = C_{30 - x}^1.C_x^2\).
Theo đề, ta có \(P\left( A \right) = \frac{{52}}{{145}}\).
\( \Leftrightarrow \frac{{C_{30 - x}^1.C_x^2}}{{C_{30}^3}} = \frac{{52}}{{145}}\).
Thay x ở các đáp án vào hệ thức trên, ta thấy x = 14 thỏa mãn.
Vậy lớp đó có 14 học sinh nữ.
Do đó ta chọn phương án D.
Câu 42:
 Xem đáp án
Xem đáp án
Gọi số cần tìm là a (a ∈ ℕ), 1000 ≤ a ≤ 9999).
Gọi x là thương khi chia a cho 5; y là thương khi chia a cho 7.
Suy ra a = 5x + 1 và a = 7y + 1.
Khi đó a – 1 = 5x và a – 1 = 7y.
Vì vậy a – 1 ∈ BC(5, 7).
Ta có BCNN(5, 7) = 35.
Suy ra BC(5, 7) = {0; 35; 70; 105; 140; ...; 980; 1015; 1050; 1085; ...}.
Vì a là số tự nhiên nhỏ nhất có 4 chữ số nên a – 1 = 1015.
Suy ra a = 1015 + 1 = 1016.
Vậy số cần tìm là 1016.
