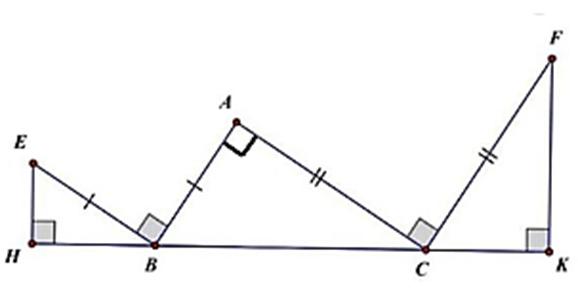
Hình vẽ bên có BE ^ BA, CF ^ CA, EH ^ BC, FK ^ BC, BE = BA và CA = CF. Chứng minh: BH = CK.
Giải bởi Vietjack
Xét ΔBHE và ΔCAB có:
\[\widehat {BHE} = \widehat {BAC} = 90^\circ \]
\[\widehat {HBE} = \widehat {BCA}\] (vì cùng phụ với \[\widehat {ABC}\])
Do đó ΔBHE ᔕ ΔCAB (g.g)
Suy ra \[\frac{{BH}}{{BE}} = \frac{{AC}}{{BC}}\]
Hay BH. BC = BE. AC = AB. AC (vì BE = AB) (1)
Tương tự ΔCKF ᔕ ΔBAC (g.g)
\[ \Rightarrow \frac{{CK}}{{CF}} = \frac{{BA}}{{BC}}\] hay CK. BC = CF. AB = AB. AC (vì CF = AC) (2)
Từ (1) và (2) suy ra BH. BC = CK. BC hay BH = CK.
Vậy BH = CK.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Từ điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MCD không đi qua tâm O và hai tiếp tuyến MA, MB đến đường tròn (O) sao cho C nằm giữa M và D. Gọi I là trung điểm của CD. Gọi K là giao điểm của các tiếp tuyến tại C và D của đường tròn (O). Chứng minh: A, B, K thẳng hàng.
Trong không gian Oxyz, cho hai điểm A(2; 2; 1), \[B\left( {\frac{{ - 8}}{3};\frac{4}{3};\frac{8}{3}} \right)\]. Viết phương trình đường thẳng đi qua tâm đường tròn nội tiếp tam giác OAB và vuông góc với mặt phẳng (OAB).
Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số cắt đường thẳng (d’): y = 2x + 1 tại điểm có hoành độ bằng –2.
Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. Tứ giác BCEQ là hình gì? Vì sao?
Cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m): y = 0,5x – 3.
Cho hình bình hành ABCD, một đường thẳng d đi qua A cắt đường chéo BD tại P, cắt các đường thẳng BC và CD lần lượt là M và N. Chứng minh BM.DN không đổi.
Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM. Chứng minh ΔKMN vuông cân.
Cho a, b, c > 0 thoả mãn \[\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 3\]. Tìm giá trị nhỏ nhất của biểu thức:
\[P = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\].
Biết tổng các hệ của khai triển (x² + 1)n bằng 1024. Hãy tìm hệ số của x¹² trong khai triển trên.
Từ bảy chữ số 1; 2; 3; 4; 5; 6; 7, lập các số có ba chữ số đôi một khác nhau. Có thể lập được bao nhiêu số như vậy?
Cho tập hợp A = {1; 2; 3; …; 10}. Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp.
Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM. So sánh hai tam giác ΔAKN và ΔBKM.
Có 2 vật M và N thoạt đầu cách nhau khoảng l. Cùng lúc 2 vật chuyển động thẳng đều, m chạy về B với vận tốc v1, N chạy về C với vận tốc v2. Tính khoảng cách ngắn nhất giữa hai vật và thời gian để đạt khoảng cách ngắn nhất giữa hai vật kể từ lúc bắt đầu chuyển động.
