Bác Kim gửi một số tiền vào ngân hàng với lãi suất là 7% và kì hạn là một năm. Sau một năm bác Kim tới ngân hàng rút cả vốn lẫn lãi được 128 400 000 đồng. Hỏi lúc đầu bác Kim gửi vào ngân hàng bao nhiêu tiền?
Giải bởi Vietjack
Gọi số tiền bác Kim gửi vào ngân hàng là x (đồng) (\[x \in {\mathbb{N}^*}\])
Số tiền lãi sau một năm là:
x.7% = 0,07x (đồng)
Sau một năm bác tới ngân hàng rút là 128 400 000 nên ta có phương trình là:
x + 0,07x = 128 400 000
⇔ 1,07x = 128 400 000
⇔ x = 120 000 000 (TMĐK)
Vậy lúc đầu bác Kim gửi vào ngân hàng 120 000 000 đồng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E; CF cắt BE tại H. Chứng minh tứ giác AEHF nội tiếp.
Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Chứng minh: ΔABH = ΔDBH.
Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H. Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF, Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu \[\widehat {BAC} = 60^\circ \], AH = 4 cm.
Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Chứng minh AH = DE.
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Cho (x + y + z)2 = x2 + y2 + z2.
Chứng minh rằng: \[\frac{1}{{{x^3}}} + \frac{1}{{{y^3}}} + \frac{1}{{{z^3}}} = \frac{3}{{xyz}}\]
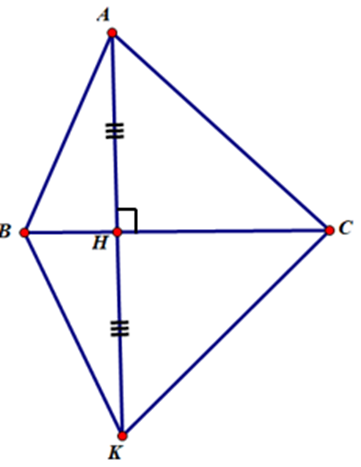
Cho tam giác ABC, kẻ AH ^ BC. Trên tia đối của tia HA, lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau trong hình vẽ.
Từ điểm M bên ngoài đường tròn (O) kẻ cát tuyến MAB (qua O) và tiếp tuyến MC, MD. Gọi K là giao của AC và BD. Chứng minh M, K, B, C cùng thuộc một đường tròn.
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Từ các chữ số 0, 1, 2, 3, 5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5, gồm 4 chữ số khác nhau?
Bà Mai vay ngân hàng 200 triệu trong thời gian 2 năm để mở một cửa hàng chuyên sản xuất và bán quà lưu niệm. Theo hợp đồng vay vốn, lãi suất vay trong một năm là 10%. Sau 1 năm, tiền lãi của năm đầu sẽ được cộng vào vốn của năm sau. Hỏi sau 2 năm, Bà Mai phải trả ngân hàng bao nhiêu tiền?
Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.
