Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với t ∈ ℤ và 0 < t ≤ 365.
(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020)
Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?
 Giải bởi Vietjack
Giải bởi Vietjack
Để thành phố A có đúng 12 giờ có ánh sáng mặt trời thì:
\(3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12 = 12\)
\( \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 0\)
\( \Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow t - 80 = 182k\,\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow t = 80 + 182k\,\,\left( {k \in \mathbb{Z}} \right)\)
Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:
\[\left\{ \begin{array}{l}k \in \mathbb{Z}\\0 < 80 + 182k \le 365\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k \in \mathbb{Z}\\ - 80 < 182k \le 285\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}k \in \mathbb{Z}\\ - \frac{{40}}{{91}} < k \le \frac{{285}}{{182}}\end{array} \right. \Leftrightarrow k \in \left\{ {0;1} \right\}\]
Với k = 0 thì t = 80 + 182.0 = 80;
Với k = 1 thì t = 80 + 182.1 = 262.
Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và ngày thứ 262 trong năm.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Giải phương trình:
\(\sin \left( {3x + \frac{\pi }{4}} \right) = - \frac{1}{2}\);
Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A0, B0 (Hình 33). Tìm hoành độ của hai giao điểm A0, B0.
![Đường thẳng dy = 1/2 cắt đồ thị hàm số y = sinx, x thuộc [-pi, pi] tại hai giao điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid1-1689066205.png)
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
3sinx + 2 = 0 trên khoảng \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\);
Giải phương trình:
\(\sin \left( {2x - \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\);
Giải phương trình:
\({\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\).
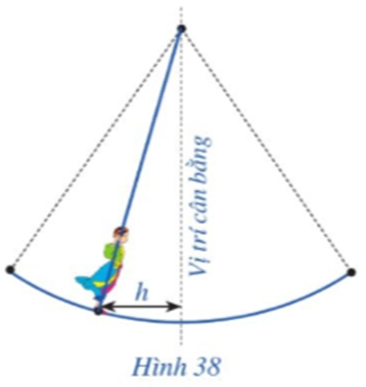
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với t ≥ 0) bởi hệ thức h = |d| với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian t nào thì khoảng cách h là 3 m, 0 m?
Quan sát các giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 (Hình 35).
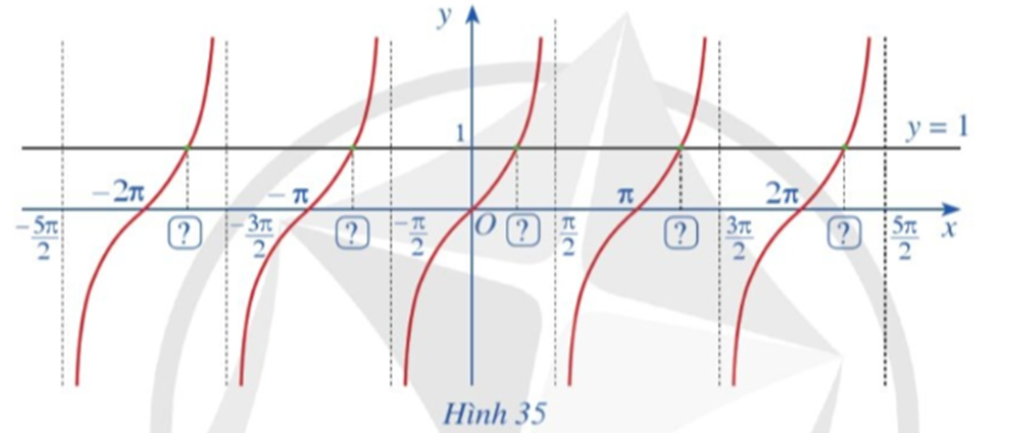
Có nhận xét gì về nghiệm của phương trình tanx = 1?