Cho hàm số $y=f\left(x\right)$ xác định và liên tục trên R, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số $y=f\left(x\right)$ trên đoạn $[-2;2]$

I. Định nghĩa

Cho hàm số y = f(x) xác định trên tập D.

a) Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu $f\left(x\right)\le M$ với mọi x thuộc D và tồn tại x_{0 $\in$} D sao cho f(x₀) = M.

Kí hiệu: $M=\underset{D}{max}f\left(x\right)$.

b) Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu $f\left(x\right)\ge m$ với mọi x thuộc D và tồn tại x₀ $\in$D sao cho f(x₀) = m.

Kí hiệu: $m=\underset{D}{min}f\left(x\right)$.

- Ví dụ 1. Cho hàm số y = f(x) có bảng biến thiên như sau:

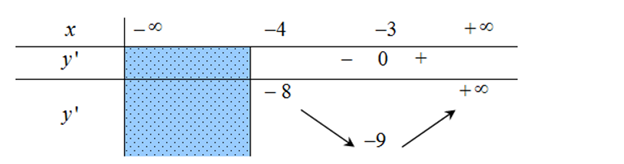
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị lớn nhất.

Giá trị nhỏ nhất của hàm số là – 9 tại x = – 3.

II. Cách tính giá trị  lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

1. Định lí.

Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn.

- Nhận xét:

Nếu đạo hàm f’(x) giữ nguyên dấu trên đoạn [a; b] thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó, f(x) đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn.

Nếu chỉ có một số hữu hạn các điểm x_i (x_i < x_{i+ 1}) mà tại đó f’(x) bằng 0 hoặc không xác định thì hàm số y = f(x) đơn điệu trên mỗi khoảng (x_i;  x_i+1). Rõ ràng, giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn [a; b] là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút a; b và tại các điểm x_i nói trên.

- Quy tắc:

1. Tìm các điểm x₁; x₂; …; x_n trên khoảng (a; b), tại đó f’(x) bằng 0 hoặc f’(x) không xác định.

2. Tính f(a); f(x₁); f(x₂); ….; f(x_n); f(b).

3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

$M=\underset{[a;b]}{max}f\left(x\right);m=\underset{[a;b]}{min}f\left(x\right)$.

- Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn hàm số $f\left(x\right)=\frac{1}{x}$ không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng (0; 1).

Tuy nhiên, cũng có những hàm số có giá trị lớn nhất hoặc giá trị nhỏ nhất trên một khoảng như ví dụ sau:

Ví dụ 2. Tìm giá trị lón nhất, nhỏ nhất của hàm số $y=\sqrt{2x-x^2}$  trên khoảng $(0;\frac{3}{2})$.

Lời giải:

Điều kiện: 2x – x² $\ge 0\iff 0\le x\le 2$.

Ta có:

$\begin{array}{c}{y}^{\text{'}}=\frac{{(2x-x^2)}^{\text{'}}}{2\sqrt{2x-x^2}}=\frac{1-x}{\sqrt{2x-x^2}}{y}^{\text{'}}=0\Rightarrow 1-x=0\iff x=1\end{array}$

Bảng biến thiên:

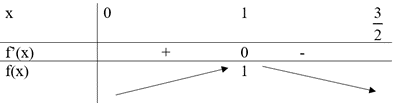
Từ bảng biến thiên trên ta thấy, trên khoảng $(0;\frac{3}{2})$ hàm số có 1 điểm cực trị duy nhất là điểm cực đại x = 1 và tại đó hàm số đạt giá trị lớn nhất $\underset{(0;\frac{3}{2})}{Max}f\left(x\right)=f\left(1\right)=1$.