Cho hàm số có đạo hàm trên R và có đồ thị như hình vẽ bên. Xét hàm số . Giá trị của tham số m để giá trị lớn nhất của hàm số g (x) trên đoạn bằng 9 là:
A. m = 10
B. m = 6
C. m = 12
D. m = 8
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Ta có:
(Do phương trình vô nghiệm)
Từ đồ thị hàm số f (x) đã cho ta có:
Hàm số g (x) trên đoạn có:
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số . Khi đó bằng
Cho hàm số liên tục trên R và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên . Giá trị của bằng:
Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tính
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ:
Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn để bất phương trình đúng với mọi x thuộc đoạn ?
Cho hàm số liên tục trên R có đồ thị như hình vẽ. Đặt . Khi đó giá trị lớn nhất của hàm số g (x) trên đoạn là:
Cho hàm số liên tục trên R và có đồ thị như hình dưới. Gọi a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của trên đoạn . Giá trị bằng:
Cho các số thực x, y thỏa mãn . Giá trị nhỏ nhất m của biểu thức là:
Cho x, y là hai số thực thỏa mãn điều kiện . Tìm giá trị lớn nhất của biểu thức
Một sợi dây kim loại dài a (cm). Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài x (cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông ( . Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất
Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số . Khi đó, giá trị của tổng M + m bằng:
Cho hàm số . Gọi M là giá trị lớn nhất của hàm số trên đoạn . Tổng các giá trị của tham số thực m để
I. Định nghĩa
Cho hàm số y = f(x) xác định trên tập D.
a) Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu với mọi x thuộc D và tồn tại x0 D sao cho f(x0) = M.
Kí hiệu: .
b) Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu với mọi x thuộc D và tồn tại x0 D sao cho f(x0) = m.
Kí hiệu: .
- Ví dụ 1. Cho hàm số y = f(x) có bảng biến thiên như sau:
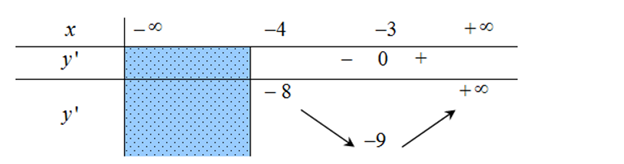
Dựa vào bảng biến thiên ta thấy, hàm số không có giá trị lớn nhất.
Giá trị nhỏ nhất của hàm số là – 9 tại x = – 3.
II. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
1. Định lí.
Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
2. Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn.
- Nhận xét:
Nếu đạo hàm f’(x) giữ nguyên dấu trên đoạn [a; b] thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó, f(x) đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn.
Nếu chỉ có một số hữu hạn các điểm xi (xi < xi+ 1) mà tại đó f’(x) bằng 0 hoặc không xác định thì hàm số y = f(x) đơn điệu trên mỗi khoảng (xi; xi+1). Rõ ràng, giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn [a; b] là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút a; b và tại các điểm xi nói trên.
- Quy tắc:
1. Tìm các điểm x1; x2; …; xn trên khoảng (a; b), tại đó f’(x) bằng 0 hoặc f’(x) không xác định.
2. Tính f(a); f(x1); f(x2); ….; f(xn); f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
.
- Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng (0; 1).
Tuy nhiên, cũng có những hàm số có giá trị lớn nhất hoặc giá trị nhỏ nhất trên một khoảng như ví dụ sau:
Ví dụ 2. Tìm giá trị lón nhất, nhỏ nhất của hàm số trên khoảng .
Lời giải:
Điều kiện: 2x – x2 .
Ta có:
Bảng biến thiên:
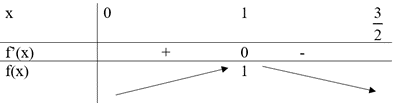
Từ bảng biến thiên trên ta thấy, trên khoảng hàm số có 1 điểm cực trị duy nhất là điểm cực đại x = 1 và tại đó hàm số đạt giá trị lớn nhất .