Giới hạn bằng
A.
B.
C. 5
D.
 Giải bởi Vietjack
Giải bởi Vietjack
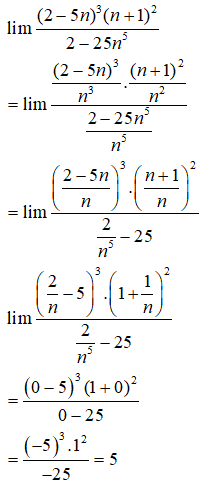
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho là một cấp số nhân công bội và số hạng đầu , Đặt . Giá trị là:
I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
1. Định nghĩa
Định nghĩa 1
Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: hay un → 0 khi n → +∞.
Ví dụ 1. Cho dãy số (un) với . Tìm giới hạn dãy số
Giải
Xét
Với n > 10 n2 > 102 = 100
.
Định nghĩa 2
Ta nói dãy số (vn) có giới hạn là a (hay vn dần tới a) khi n → +∞ nếu
Kí hiệu: hay vn → a khi n → +∞.
Ví dụ 2. Cho dãy số . Chứng minh rằng .
Giải
Ta có
Do đó: .
2. Một vài giới hạn đặc biệt
a) với k nguyên dương;
b) nếu |q| < 1;
c) Nếu un = c (c là hằng số) thì .
Chú ý: Từ nay về sau thay cho ta viết tắt là lim un = a.
II. ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN
Định lí 1
a) Nếu lim un = a và lim vn = b thì
lim (un + vn) = a + b
lim (un – vn) = a – b
lim (un.vn) = a.b
(nếu )
Nếu với mọi n và limun = a thì:
và
Ví dụ 3. Tính
Giải
Ví dụ 4. Tìm
Giải
III. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
Cấp số nhân vô hạn (un) có công bội q, với |q| < 1 được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn:
Ví dụ 5. Tính tổng của cấp số nhân lùi vô hạn
Giải
Ta có dãy số là một số cấp số nhân lùi vô hạn với công bội .
Khi đó ta có:
IV. GIỚI HẠN VÔ CỰC
1. Định nghĩa
- Ta nói dãy số (un) có giới hạn là +∞ khi n → +∞, nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: lim un = +∞ hay un → +∞ khi n → +∞.
- Dãy số (un) có giới hạn là –∞ khi n → +∞, nếu lim (–un) = +∞.
Kí hiệu: lim un = –∞ hay un → –∞ khi n → +∞.
Nhận xét: un = +∞ ⇔ lim(–un) = –∞
2. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau
a) lim nk = +∞ với k nguyên dương;
b) lim qn = +∞ nếu q > 1.
3. Định lí 2
a) Nếu lim un = a và lim vn = ±∞ thì
b) Nếu lim un = a > 0, lim vn = 0 và vn > 0, ∀ n > 0 thì
c) Nếu lim un = +∞ và lim vn = a > 0 thì .
Ví dụ 6. Tính .
Giải
Vì và